+云南省昭通市2023-2024学年八年级上学期期末数学试卷

这是一份+云南省昭通市2023-2024学年八年级上学期期末数学试卷，共18页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1．（3分）下列长度的三条线段（单位：cm），能组成三角形的是（ ）
A．1，2，4B．2，4，6C．2，6，7D．5，7，13
2．（3分）要使分式有意义，x应满足的条件是（ ）
A．x＞﹣3B．x＜﹣3C．x≠﹣3D．x＝﹣3
3．（3分）对称美是我国古人和谐平衡思想的体现，常被运用于建筑、器物、绘画、标识等作品的设计上，使对称之美惊艳了千年的时光．下列图案是轴对称图形的是（ ）
A．B．C．D．
4．（3分）下列运算中，正确的是（ ）
A．a2+2a3＝3a5B．a2•a3＝a6
C．（﹣a2）4＝﹣a8D．a8÷a6＝a2
5．（3分）在平面直角坐标系中，点（3，2）关于x轴对称的点是（ ）
A．（﹣3，2）B．（3，﹣2）C．（﹣3，﹣2）D．（﹣2，3）
6．（3分）石墨烯具有优异的光学、电学、力学特性，在材料学、微纳加工、能源、生物医学和药物传递等方面具有重要的应用前景，被认为是一种未来革命性的材料．石墨烯中每两个相邻碳原子间的键长为0.0000000142cm（ ）
A．1.42×10﹣7B．1.42×10﹣8
C．0.142×10﹣7D．1.42×10﹣9
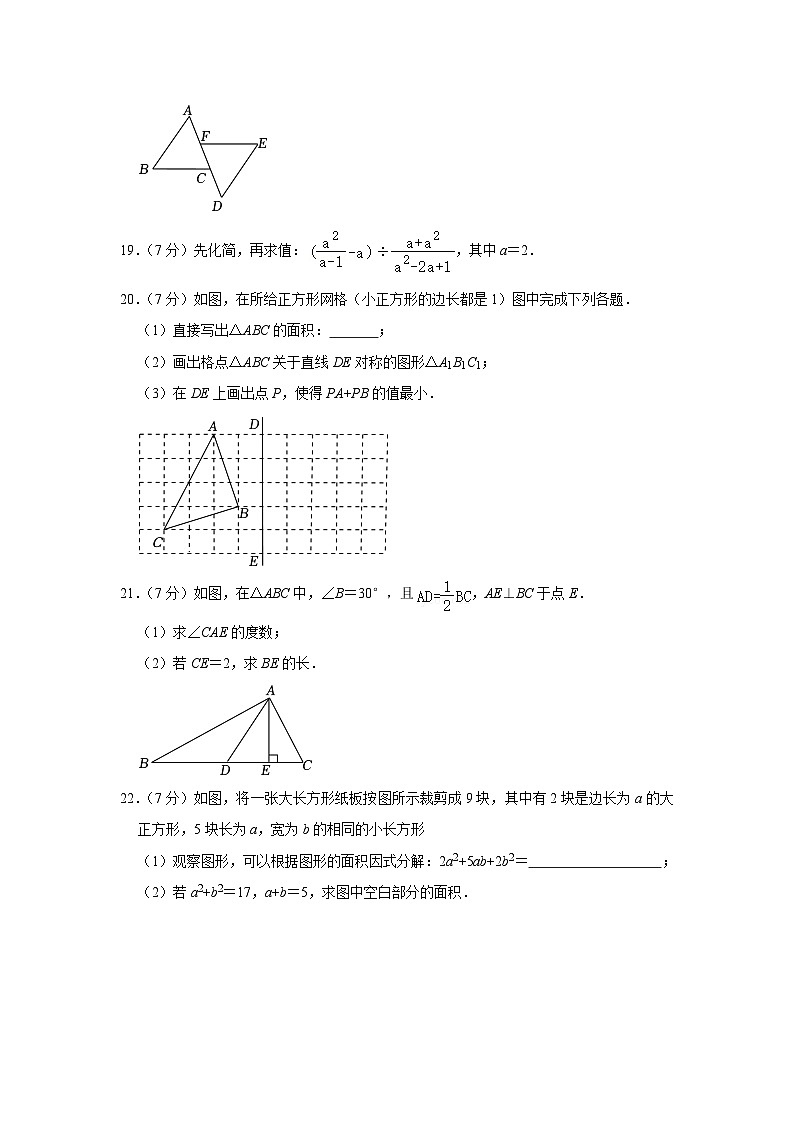
7．（3分）如图，已知CB＝FE，∠CBA＝∠FED（ ）
A．AC＝DFB．AB＝DEC．∠C＝∠FD．AC∥DF
8．（3分）若x2+mx+16＝（x﹣4）2，则m的值是（ ）
A．4B．8C．﹣8D．±8
9．（3分）一个多边形的内角和为1260°，则这个多边形是（ ）
A．七边形B．八边形C．九边形D．十边形
10．（3分）已知x﹣y＝7，xy＝5，则（x+1）（1﹣y）的值为（ ）
A．13B．3C．﹣11D．﹣13
11．（3分）如图，点B、D、E、C在同一直线上，△ABD≌△ACE，则∠DAE＝（ ）
A．10°B．20°C．30°D．80°
12．（3分）某列车提速前行驶400km与提速后行驶500km所用时间相同，若列车平均提速20km/h，设提速后平均速度为x km/h（ ）
A．＝B．＝
C．＝D．＝
二、填空题（本大题共4小题，每小题2分，共8分）
13．（2分）等边三角形的一个外角度数为 ．
14．（2分）因式分解：x2﹣4＝ ．
15．（2分）如图，在△ABC中，DE是AC的垂直平分线，△ABD的周长为10，则△ABC的周长为 ．
16．（2分）若关于x的分式方程有增根，则m的值为 ．
三、解答题（本大题共8小题，共56分）
17．（6分）计算：．
18．（6分）如图，已知点C，F在直线AD上，AB＝DE，CD＝AF．求证：△ABC≌△DEF．
19．（7分）先化简，再求值：，其中a＝2．
20．（7分）如图，在所给正方形网格（小正方形的边长都是1）图中完成下列各题．
（1）直接写出△ABC的面积： ；
（2）画出格点△ABC关于直线DE对称的图形△A1B1C1；
（3）在DE上画出点P，使得PA+PB的值最小．
21．（7分）如图，在△ABC中，∠B＝30°，且，AE⊥BC于点E．
（1）求∠CAE的度数；
（2）若CE＝2，求BE的长．
22．（7分）如图，将一张大长方形纸板按图所示裁剪成9块，其中有2块是边长为a的大正方形，5块长为a，宽为b的相同的小长方形
（1）观察图形，可以根据图形的面积因式分解：2a2+5ab+2b2＝ ；
（2）若a2+b2＝17，a+b＝5，求图中空白部分的面积．
23．（8分）如图，已知点P在∠AOB的平分线上，点C、D分别在射线OA、OB上（1）当PC⊥OA，PD⊥OB时 ；
（2）当∠AOB＝90°，且PC⊥PD时，（1）中的数量关系还成立吗？请说明理由；
（3）在（2）条件下，若OC+OD＝6 ．
24．（8分）观察下列等式：
第一个等式：；
第二个等式：；
第三个等式；；
第四个等式：……
探索规律，解答下列问题：
（1）用含n的式子表示第n个等式；
（2）若代数式的值为正整数，求整数x的值．
2023-2024学年云南省昭通市八年级（上）期末数学试卷
参考答案与试题解析
一、选择题（本大题共12小题，每小题3分，共36分）
1．（3分）下列长度的三条线段（单位：cm），能组成三角形的是（ ）
A．1，2，4B．2，4，6C．2，6，7D．5，7，13
【分析】根据三角形三边关系定理判断即可．
【解答】解：A．∵1+2＜5，故A不符合题意；
B．∵2+4＝7，故B不符合题意；
C．∵2+6＞6，故C符合题意
D．∵5+7＜13，故D不符合题意；
故选：C．
【点评】本题考查的是三角形的三边关系，掌握三角形三边关系定理：三角形两边之和大于第三边是解题的关键．
2．（3分）要使分式有意义，x应满足的条件是（ ）
A．x＞﹣3B．x＜﹣3C．x≠﹣3D．x＝﹣3
【分析】根据分式有意义的条件是分母不等于零可得答案．
【解答】解：由题意得：x+3≠0，
解得：x≠﹣2，
故选：C．
【点评】此题主要考查了分式有意义的条件，关键是掌握分式有意义的条件是分母不等于零．
3．（3分）对称美是我国古人和谐平衡思想的体现，常被运用于建筑、器物、绘画、标识等作品的设计上，使对称之美惊艳了千年的时光．下列图案是轴对称图形的是（ ）
A．B．C．D．
【分析】根据如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形，这条直线叫做对称轴进行分析即可．
【解答】解：A，C，D选项中的图形不都能找到这样的一条直线，直线两旁的部分能够互相重合；
B选项中的图形能找到这样的两条直线，使图形沿一条直线折叠，所以是轴对称图形；
故选：B．
【点评】本题考查了轴对称图形的概念，轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合．
4．（3分）下列运算中，正确的是（ ）
A．a2+2a3＝3a5B．a2•a3＝a6
C．（﹣a2）4＝﹣a8D．a8÷a6＝a2
【分析】根据合并同类项法则，同底数幂相乘，底数不变指数相加；幂的乘方，底数不变，指数相乘；同底数幂相除，底数不变，指数相减，对各选项分析判断后利用排除法求解．
【解答】解：A、a2与2a8不是同类项，不能合并；
B、a2•a3＝a8，故此选项不符合题意；
C、（﹣a2）4＝a5，故此选项不符合题意；
D、a8÷a6＝a3，故此选项符合题意；
故选：D．
【点评】本题考查合并同类项、同底数幂的乘法、幂的乘方、同底数幂的除法，熟练掌握运算性质和法则是解题的关键．
5．（3分）在平面直角坐标系中，点（3，2）关于x轴对称的点是（ ）
A．（﹣3，2）B．（3，﹣2）C．（﹣3，﹣2）D．（﹣2，3）
【分析】根据“关于x轴对称的点，横坐标相同，纵坐标互为相反数”解答即可．
【解答】解在平面直角坐标系中，点（3，﹣2）．
故选：B．
【点评】本题考查了关于x轴、y轴对称的点的坐标，解决本题的关键是掌握好对称点的坐标规律：（1）关于x轴对称的点，横坐标相同，纵坐标互为相反数；（2）关于y轴对称的点，纵坐标相同，横坐标互为相反数；（3）关于原点对称的点，横坐标与纵坐标都互为相反数．
6．（3分）石墨烯具有优异的光学、电学、力学特性，在材料学、微纳加工、能源、生物医学和药物传递等方面具有重要的应用前景，被认为是一种未来革命性的材料．石墨烯中每两个相邻碳原子间的键长为0.0000000142cm（ ）
A．1.42×10﹣7B．1.42×10﹣8
C．0.142×10﹣7D．1.42×10﹣9
【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值≥10时，n是正整数；当原数的绝对值＜1时，n是负整数．
【解答】解：0.0000000142＝1.42×10﹣3．
故选：B．
【点评】此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，正确确定a的值以及n的值是解决问题的关键．
7．（3分）如图，已知CB＝FE，∠CBA＝∠FED（ ）
A．AC＝DFB．AB＝DEC．∠C＝∠FD．AC∥DF
【分析】根据全等三角形的判定方法依次进行判断即可．
【解答】解：∵CB＝FE，∠CBA＝∠FED，
添加AC＝DF，不能判定△ABC≌△DEF，
故A选项符合题意；
添加AB＝DC，根据SAS可证△ABC≌△DEF，
故B选项不符合题意；
添加∠C＝∠F，根据ASA可证△ABC≌△DEF，
故C选项不符合题意；
添加AC∥DF，可得∠A＝∠FDE，
根据AAS可证△ABC≌△DEF，
故D选项不符合题意，
故选：A．
【点评】本题考查了全等三角形的判定，熟练掌握全等三角形的判定方法是解题的关键．
8．（3分）若x2+mx+16＝（x﹣4）2，则m的值是（ ）
A．4B．8C．﹣8D．±8
【分析】根据完全平方公式展开等号右边的式子，然后根据等号左右对应相等即可求得m的值．
【解答】解：∵x2+mx+16＝（x﹣4）2，
∴x2+mx+16＝x2﹣6x+16，
∴m＝﹣8，
故选：C．
【点评】本题考查公式法，解答本题的关键是明确题意，利用完全平方公式解答．
9．（3分）一个多边形的内角和为1260°，则这个多边形是（ ）
A．七边形B．八边形C．九边形D．十边形
【分析】n边形的内角和可以表示成（n﹣2）•180°，设这个多边形是n边形，就可以列出方程（n﹣2）•180°＝1260°，即可解得n的值．
【解答】解：设这个多边形是n边形，
根据题意得：（n﹣2）•180°＝1260°，
解得：n＝9，
则这个多边形是九边形．
故选：C．
【点评】本题考查了对于多边形内角，解题关键是掌握多边形外交和公式．
10．（3分）已知x﹣y＝7，xy＝5，则（x+1）（1﹣y）的值为（ ）
A．13B．3C．﹣11D．﹣13
【分析】先根据多项式乘多项式法则将式子展开，再将x﹣y＝7，xy＝5整体代入即可求解．
【解答】解：（x+1）（1﹣y）
＝x﹣xy+3﹣y
＝x﹣y﹣xy+1，
∵x﹣y＝7，xy＝8，
∴原式＝7﹣5+7＝3，
故选：B．
【点评】本题主要考查多项式乘多项式，掌握多项式乘多项式法则及运用整体代入思想是解题的关键．
11．（3分）如图，点B、D、E、C在同一直线上，△ABD≌△ACE，则∠DAE＝（ ）
A．10°B．20°C．30°D．80°
【分析】根据全等三角形的性质可得AD＝AE，进一步可得∠ADE＝∠AED，求出∠AED的度数，根据三角形内角和定理可得∠DAE的度数．
【解答】解：∵△ABD≌△ACE，
∴AD＝AE，
∴∠ADE＝∠AED，
∵∠AEC＝100°，
∴∠AED＝80°，
∴∠ADE＝80°，
∴∠DAE＝180°﹣80°﹣80°＝20°，
故选：B．
【点评】本题考查了全等三角形的性质，三角形的内角和定理等，熟练掌握全等三角形的性质是解题的关键．
12．（3分）某列车提速前行驶400km与提速后行驶500km所用时间相同，若列车平均提速20km/h，设提速后平均速度为x km/h（ ）
A．＝B．＝
C．＝D．＝
【分析】根据动车提速前后速度间的关系，可得出动车提速前的平均速度为（x﹣20）km/h，利用时间＝路程÷速度，结合动车提速后行驶400km与提速后行驶500km所用的时间相同，即可动出关于x的分式方程，此题得解．
【解答】解：∵提速后平均速度为x km/h，且动车平均提速20km/h，
∴动车提速前的平均速度为（x﹣20）km/h．
根据题意得：＝．
故选：C．
【点评】本题考查了由实际问题抽象出分式方程，找准等量关系，正确列出分式方程是解题的关键．
二、填空题（本大题共4小题，每小题2分，共8分）
13．（2分）等边三角形的一个外角度数为 120° ．
【分析】根据等边三角形的性质进行计算，即可解答．
【解答】解：等边三角形的一个外角度数＝180°﹣60°＝120°，
故答案为：120°．
【点评】本题考查了等边三角形的性质，熟练掌握等边三角形的性质是解题的关键．
14．（2分）因式分解：x2﹣4＝ （x+2）（x﹣2） ．
【分析】直接利用平方差公式分解因式得出答案．
【解答】解：x2﹣4＝（x+3）（x﹣2）．
故答案为：（x+2）（x﹣6）．
【点评】此题主要考查了公式法分解因式，正确应用平方差公式是解题关键．
15．（2分）如图，在△ABC中，DE是AC的垂直平分线，△ABD的周长为10，则△ABC的周长为 14 ．
【分析】根据线段垂直平分线的性质得到DA＝DC，AC＝2AE＝4，根据三角形的周长公式计算即可．
【解答】解：∵DE是AC的垂直平分线，AE＝2，
∴DA＝DC，AC＝2AE＝3，
∵△ABD的周长为10，
∴AB+BD+AD＝10，
∴AB+BD+DC＝AB+BC＝10，
∴△ABC的周长＝AB+BC+AC＝10+4＝14，
故答案为：14．
【点评】本题考查的是线段的垂直平分线的性质，掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键．
16．（2分）若关于x的分式方程有增根，则m的值为 ﹣2 ．
【分析】根据题意可得：x+1＝0，从而可得x＝﹣1，然后把x的值代入整式方程中进行计算，即可解答．
【解答】解：，
x﹣1＝m﹣7（x+1），
解得：x＝，
∵分式方程有增根，
∴x+1＝0，
∴x＝﹣7，
把x＝﹣1代入x＝中得：，
解得：m＝﹣8，
故答案为：﹣2．
【点评】本题考查了分式方程的增根，根据题意求出x的值后代入整式方程中进行计算是解题的关键．
三、解答题（本大题共8小题，共56分）
17．（6分）计算：．
【分析】先根据乘方的意义、零指数幂和负整数指数幂的意义计算，然后化简后进行有理数的加减运算．
【解答】解：原式＝1+5﹣8+4
＝9．
【点评】本题考查了二次根式的混合运算，熟练掌握二次根式的性质、零指数幂和负整数指数幂是解决问题的关键．
18．（6分）如图，已知点C，F在直线AD上，AB＝DE，CD＝AF．求证：△ABC≌△DEF．
【分析】首先根据CD＝AF可得CD+CF＝AF+CF，即AC＝DF，可利用SSS证明△ABC≌△DEF．
【解答】证明：∵CD＝AF，
∴CD+CF＝AF+CF，即AC＝DF，
在△ABC和△DEF中，
，
∴△ABC≌△DEF（SSS）．
【点评】此题主要考查了全等三角形的判定，关键是掌握判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．
19．（7分）先化简，再求值：，其中a＝2．
【分析】根据分式的减法法则、除法法则把原式化简，把a的值代入计算即可．
【解答】解：原式＝（﹣）÷
＝•
＝，
当a＝2时，原式＝＝．
【点评】本题考查的是分式的化简求值，掌握分式的混合运算法则是解题的关键．
20．（7分）如图，在所给正方形网格（小正方形的边长都是1）图中完成下列各题．
（1）直接写出△ABC的面积： 5 ；
（2）画出格点△ABC关于直线DE对称的图形△A1B1C1；
（3）在DE上画出点P，使得PA+PB的值最小．
【分析】（1）利用割补法求三角形的面积即可．
（2）根据轴对称的性质作图即可．
（3）连接AB1，交直线DE于点P，则点P即为所求．
【解答】解：（1）△ABC的面积为＝8﹣．
故答案为：5．
（2）如图，△A1B2C1即为所求．
（3）如图，连接AB1，交直线DE于点P，
此时PA+PB＝PA+PB4＝AB1，为最小值，
则点P即为所求．
【点评】本题考查作图﹣轴对称变换、轴对称﹣最短路线问题，熟练掌握轴对称的性质是解答本题的关键．
21．（7分）如图，在△ABC中，∠B＝30°，且，AE⊥BC于点E．
（1）求∠CAE的度数；
（2）若CE＝2，求BE的长．
【分析】（1）根据中线的定义推出AD＝BD＝CD，根据等腰三角形的性质及三角形外角性质求出∠ADC＝60°，即可判定△ACD是等边三角形，根据等边三角形的性质及直角三角形的性质求解即可；
（2）根据含30°角的直角三角形的性质求解即可．
【解答】解：（1）∵AD是BC边上的中线，
∴BD＝CD＝BC，
∵AD＝BC，
∴AD＝BD＝CD，
∴∠B＝∠BAD＝30°，
∴∠ADC＝∠B+∠BAD＝60°，
∴△ACD是等边三角形，
∴∠DAC＝∠C＝60°，
∵AE⊥BC，
∴∠AEC＝90°，
∴∠C+∠CAE＝90°，
∴∠CAE＝30°；
（2）在Rt△ACE中，CE＝2，
∴AC＝5CE＝4，
∵∠BAC＝∠BAD+∠DAC＝90°，∠B＝30°，
∴BC＝2AC＝8，
∴BE＝BC﹣CE＝6．
【点评】此题考查了直角三角形斜边上的中线、含30°角的直角三角形的性质，熟记直角三角形斜边上的中线、含30°角的直角三角形的性质是解题的关键．
22．（7分）如图，将一张大长方形纸板按图所示裁剪成9块，其中有2块是边长为a的大正方形，5块长为a，宽为b的相同的小长方形
（1）观察图形，可以根据图形的面积因式分解：2a2+5ab+2b2＝ （2a+b）（a+2b） ；
（2）若a2+b2＝17，a+b＝5，求图中空白部分的面积．
【分析】（1）2块边长为a的大正方形的面积+2块边长为b的小正方形的面积+5块长为a，宽为b的相同的小长方形的面积＝长为（2a+b），宽为（a+2b）的大长方形的面积；
（2）由a2+b2＝17，a+b＝5，可得ab，空白部分的面积即5块长为a，宽为b的相同的小长方形的面积．
【解答】解：（1）2a2+6ab+2b2＝（4a+b）（a+2b），
故答案为：（2a+b）（a+6b）；
（2）∵a2+b2＝17，a+b＝7，
∴ab＝[（a+b）2﹣（a2+b2）]＝4，
空白部分的面积＝5×ab＝20．
【点评】本题考查了因式分解，观察图形辅助理解因式分解是本题的关键．
23．（8分）如图，已知点P在∠AOB的平分线上，点C、D分别在射线OA、OB上（1）当PC⊥OA，PD⊥OB时 PC＝PD ；
（2）当∠AOB＝90°，且PC⊥PD时，（1）中的数量关系还成立吗？请说明理由；
（3）在（2）条件下，若OC+OD＝6 9 ．
【分析】（1）根据角平分线性质可知PC＝PD；
（2）过点P点作PE⊥OA于E，PF⊥OB于F，根据垂直的定义得到∠PEC＝∠PFD＝90°，由OM是∠AOB的平分线，根据角平分线的性质得到PE＝PF，利用四边形内角和定理可得到∠PCE+∠PDO＝360°﹣90°﹣90°＝180°，而∠PDO+∠PDF＝180°，则∠PCE＝∠PDF，然后根据“AAS”可判断△PCE≌△PDF，根据全等的性质即可得到PC＝PD；
（3）根据全等三角形的性质推出四边形OFPE是正方形，由S四边形ODPC＝S四边形OFPE＝9．即可得出结论．
【解答】解：（1）∵OM是∠AOB的平分线，PC⊥OA，
∴PC＝PD（角平分线上点到角两边的距离相等），
故答案为：PC＝PD；
（2）成立，理由如下：
过点P点作PE⊥OA于E，PF⊥OB于F，
∴∠PEC＝∠PFD＝90°，
∵OM是∠AOB的平分线，
∴PE＝PF，
∵∠AOB＝90°，∠CPD＝90°，
∴∠PCE+∠PDO＝360°﹣90°﹣90°＝180°，
∵∠PDO+∠PDF＝180°，
∴∠PCE＝∠PDF，
在△PCE和△PDF中，
，
∴△PCE≌△PDF（AAS），
∴PC＝PD；
（3）由（2）可知，△PCE≌△PDF，
∴CE＝DF，
∵OC+OD＝6，
∴OE+CE+OD＝DF+OE+OD＝OE+OF＝6，
在Rt△OPE和Rt△OPF中，
，
∴Rt△OPE≌Rt△OPF（HL），
∴OE＝OF＝5，
∴四边形OFPE是正方形，
∴S四边形ODPC＝S四边形OFPE＝9．
故答案为：9．
【点评】本题主要考查了角平分线的性质，三角形全等的判定与性质，四边形的面积的转化，掌握由角平分线联想到对应辅助线，进而作出合适的辅助线是解题的关键．
24．（8分）观察下列等式：
第一个等式：；
第二个等式：；
第三个等式；；
第四个等式：……
探索规律，解答下列问题：
（1）用含n的式子表示第n个等式；
（2）若代数式的值为正整数，求整数x的值．
【分析】（1）根据所给等式，发现各部分的变化规律即可解决问题．
（2）依据（1）中发现的规律即可解决问题．
【解答】解：（1）观察所给等式各部分的变化规律可知，
第n个等式为：；
（2）由（1）可知，
＝
＝
＝．
则原式＝
＝．
因为的值是正整，
所以x﹣1＝1或7或4，
则x＝2或4或5．
故正整数x的值为2或5或5．
【点评】本题考查数字变化的规律，能根据所给等式各部分的变化规律，用含n的式子表示第n个等式是解题的关键．
声明：试题解析著作权属所有，未经书面同意，不得复制发布日期：2024/1/17 9:04:14；用户：娄老师；邮箱：15225657626；学号：48669677