河北省邯郸市馆陶县2022-2023学年八年级下学期期末考试数学试卷(含答案)

这是一份河北省邯郸市馆陶县2022-2023学年八年级下学期期末考试数学试卷(含答案)，共10页。试卷主要包含了本试题共6页，满分120分．，点在轴上，则下列说法正确的是，正比例函数的图象大致是等内容，欢迎下载使用。

说明：
1.本试题共6页，满分120分．
2.请将所有答案填写在答题卡上，答在本试卷上无效．
一、选择题（本大题共14个小题，每小题3分，共42分．在每小题给出的四个选项中，只有一项是符合题目要求的）
1.要画一个面积为长方形，其长为，宽为，在这一变化过程中，下列说法正确的是（ ）
A.30是常量 B.是常量 C.30是变量 D.是常量
2.某班进行民主选举班干部，要求每位同学选出一位候选人，并将其选票投入票箱．这个过程是收集数据中的（ ）
A.确定调查对象 B.实施调查
C.选择调查方法 D.得出结论
3.用长分别为的四根木根，恰好能钉成一个平行四边形的木框（接头忽略不记），则的值是（ ）
A.5 B.7 C.2 D.12
4.点在轴上，则下列说法正确的是（ ）
A. B. C. D.
5.一组数据有90个，其中最大值为141，最小值为40，取组距为10，则可以分成（ ）
A.9组 B.10组 C.11组 D.12组
6.如图所示，某居民小区为了美化环境，要在一块三角形ABC空地上围一个四边形花坛BCFE，已知点E、F分别是边AB、AC的中点，量得BC=16米，则边EF的长是（ ）
A.6米 B.7米 C.8米 D.9米
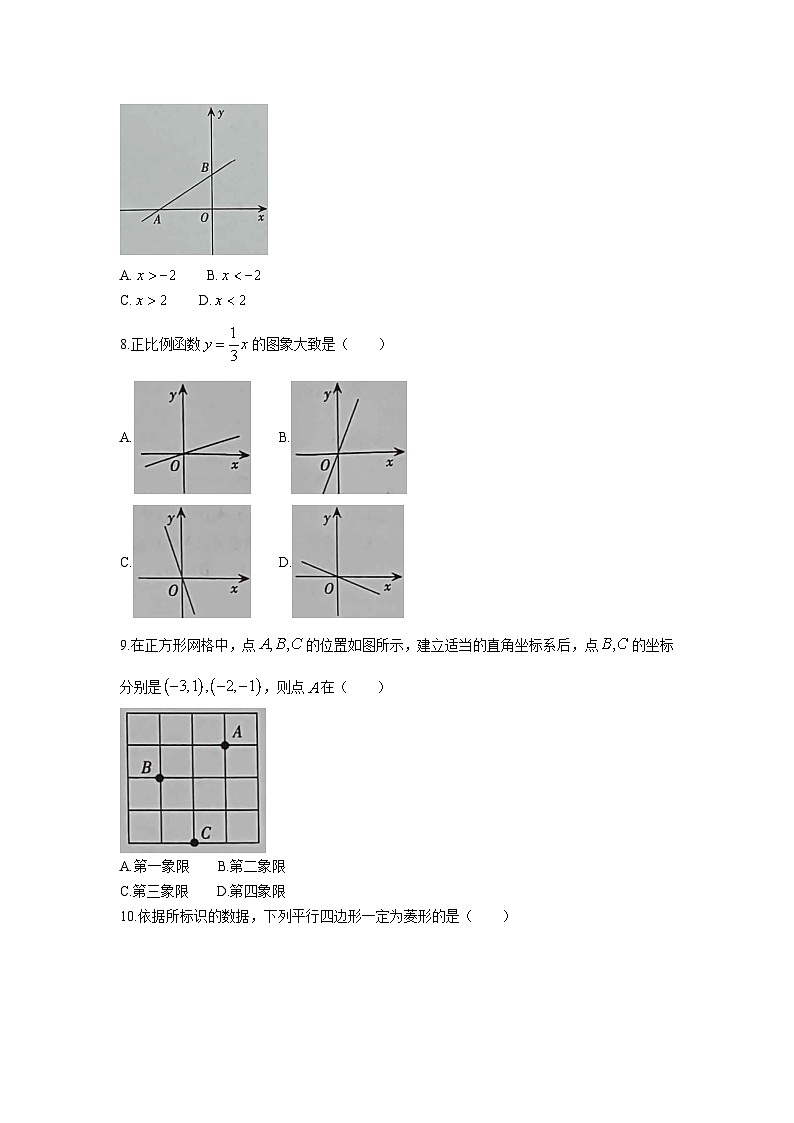
7.如图，直线交坐标轴于两点，则不等式的解集为（ ）
A. B.
C. D.
8.正比例函数的图象大致是（ ）
A. B.
C. D.
9.在正方形网格中，点的位置如图所示，建立适当的直角坐标系后，点的坐标分别是，则点在（ ）
A.第一象限 B.第二象限
C.第三象限 D.第四象限
10.依据所标识的数据，下列平行四边形一定为菱形的是（ ）
A. B.
C. D.
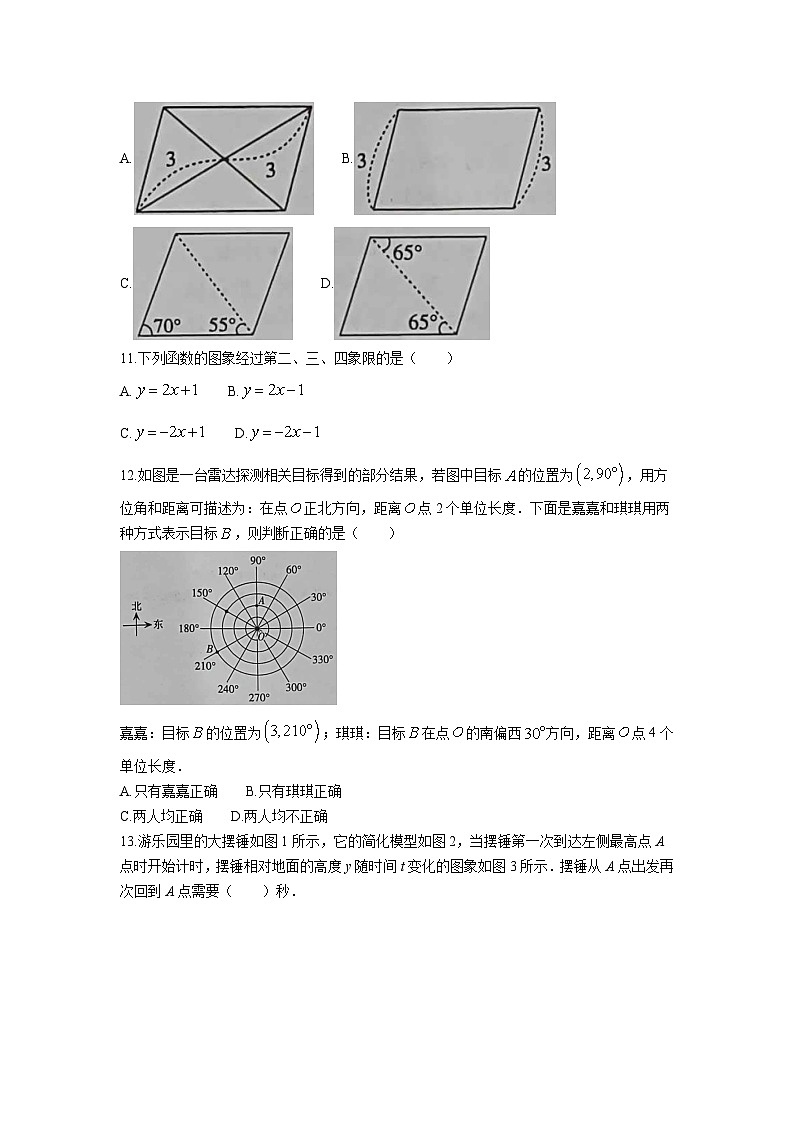
11.下列函数的图象经过第二、三、四象限的是（ ）
A. B.
C. D.
12.如图是一台雷达探测相关目标得到的部分结果，若图中目标的位置为，用方位角和距离可描述为：在点正北方向，距离点2个单位长度．下面是嘉嘉和琪琪用两种方式表示目标，则判断正确的是（ ）
嘉嘉：目标的位置为；琪琪：目标在点的南偏西方向，距离点4个单位长度．
A.只有嘉嘉正确 B.只有琪琪正确
C.两人均正确 D.两人均不正确
13.游乐园里的大摆锤如图1所示，它的简化模型如图2，当摆锤第一次到达左侧最高点A点时开始计时，摆锤相对地面的高度y随时间t变化的图象如图3所示．摆锤从A点出发再次回到A点需要（ ）秒．
A.2 B.4 C.6 D.8
14.已知等腰三角形的周长为16，设底边长为，腰长为．可得出关于的函数表达式为，对于自变量的取值范围，小丽、小强给出不同的解答：
小丽：由于是底边长，因此
小强：由于三角形两边和大于第三边，因此，解得，对于两人的解法，正确的是（ ）
A.小丽对
B.小强对
C.小丽和小强合在一起对
D.小丽和小强合在一起也不对
二、填空题（本大题共3个小题，每小题3分，共9分．其中16小题第一空2分，第二空1分；17小题每空1分，请将答案直接写在题中横线上）
15.在平面直角坐标系中，点到原点的距离为__________．
16.某校为了解今年春季开学后八年级学生的体质情况，校卫生室从八年级19个班中随机抽取了190名学生进行调研，则此次抽样调查的样本是__________，样本容量是__________．
17.如图1，点为矩形中边的中点，点从点出发，沿以的速度运动到点，图2是点运动时，的面积随时间变化的函数图象，
（1）__________；
（2）点到的距离是__________；
（3）的值为__________．
三、解答题（本大题共七个小题，满分69分，解答题应写出必要的解题步骤或文字说明）
18.（本小题满分9分）
如图所示，在直角坐标系中，已知三点的坐标分别为．
（1）点关于轴的对称点的坐标是__________；
（2）画出把向右平移6个单位，再向上平移1个单位的图形；并写出点对应点的坐标；
19.（本小题满分9分）
已知一个多边形的内角和等于它的外角和的2倍．
（1）求这个多边形的内角和．
（2）求这个多边形的边数．
20.（本小题满分9分）
为了解我市初中生每周锻炼身体的时长t（单位：小时）的情况，在全市随机抽取部分初中生进行调查，按五个组别：A组组组组组进行整理，绘制如下两幅不完整的统计图，
根据图中提供的信息，解决下列问题：
（1）求抽样调查的学生总人数；
（2）抽取的学生中，求D组的频数；
（3）求D组所在扇形的圆心角．
21.（本小题满分10分）
如图，点是平行四边形对角线的交点，，分别过点作，连接．
（1）求证：四边形是矩形；
（2）设，求的长．
22.（本小题满分10分）
某企业接到一批订单，在160天内（含160天）生产甲、乙两种型号家具共100套，经过测试与统计，得到如下数据：
受条件限制，两种型号的家具不能同时生产，已知该企业能如期完成生产任务，设生产甲型家具套，生产这100套家具的总利润为（万元）．
（1）求与之间的函数关系式；
（2）求为何值时，最大，最大值是多少？
23.（本小题满分10分）
某数学学习网站，正在讲解如下问题：
【背景呈现】在平面直角坐标系中，直线经过，直线与轴交于点，与直线交于点
【解决问题】
（1）求直线的函数解析式；
（2）求的面积；
【拓展探究】嘉淇为了更好观看图象，用手机截屏该问题的图象，如图所示，嘉淇发现屏幕上有一位置固定的黑点M，刚好落在直角坐标系中坐标为的位置上，嘉淇通过手机的触屏功能，在坐标原点的位置与可视范围不改变的情况下，把截屏横向、纵向放大相同的倍数，当直线恰好经过点M时，图中坐标系的单位长度变为原来的a倍，直接写出a的值；
24.（本小题满分12分）
如图，在正方形中，是上的一点（不与端点重合），连结，过点作的垂线，垂足为，延长交于点．在上取点，使得，连结．
（1）求证：；
（2）①若，则__________；
②改变的度数，的度数是否会发生变化？若发生变化，请写出与之间的数量关系，若不改变，请说明理由；
（3）若，直接写出的长．
2022-2023学年第二学期期末文化课水平测试
八年级数学参考答案（冀教版）
1-5ABBAC 6-10CAABC 11-14DDDC
15.5
16.190名学生的体质情况，190
17.（1）90°（2）6（3）4
18.解：（1）（-4，-3）
（2）
写出A点对应点A′的坐标（5，6）
19.解：（1）这个多边形的内角和为360°×2=720°．
（2）设这个多边形的边数为x．
根据多边形内角和公式，得180°（x-2）=720°．
∴x=6.
∴这个多边形的边数为6
20.（1）抽样调查的学生总人数为100÷20%=500（人）
（2）500-（50+100+160+40）=150（人）
（3）D组所在扇形的圆心角度数为360°×=108°
21.（1）证明：∵CE∥BD，DE∥AC，∴四边形OCED是平行四边形，
∵四边形ABCD是平行四边形，AB=BC，∴平行四边形ABCD是菱形，
∴AC⊥BD，∴∠COD=90°，
∴平行四边形OCED是矩形；
（2）解：∵四边形ABCD是平行四边形，AC=12，BD=16，
∴OC=AC=6，OD=BD=8，
在Rt△COD中，由勾股定理得：CD=，
由（1）知，四边形OCED是矩形，
∴OE=CD=10
22.解：（1）∵y=0.5x+0.8（100-x）=-0.3x+80
（2）由题意得，x+（100-x）≤160
解之得，x≥16
∵，y随x增大而减小，
∴x=16时，y最大，最大值为-0.3×16+80=75.2（万元）
23.
（1）设直线l1的函数解析式为
∵点A（-3，4），B（3，0）在直线l1上，
∴
解这个方程组，得
∴直线l1的函数解析式为
（2）∵直线l2：与x轴交于点C，∴，∴C（-2，0）
∵直线l2：与直线l1交于点D，∴，解这个方程组，
得，∴D的坐标为（，）
∴△BCD的面积=
【拓展探究】3
24.（1）证明：∵四边形ABCD是正方形，∴AD=AB，∠BAD=∠CBA=90°，
∴∠DAF+∠EAF=90°，∵DE⊥AH，∴∠AFD=∠DAF+∠ADF=90°，
∴∠ADE=∠BAH，∴△ADE≌△BAH；
（2）①45°
②∠HGC的度数不会发生变化，
理由如下：∵DE⊥AH于F，FA=FG，∴AD=DG
设∠ADE=α，则∠DAF=∠DGF=90°-α，
∴∠FDG=α，
∴∠CDG=90°-2α，∠DGH=90°+α，
∴∠DCG=∠DGC==45°+α，
∴∠HGC=∠DGH-∠DGC=90°+α-（45°+α）=45°，
∴∠HGC的度数不会发生变化；
（3）
如图2，过点C作CM⊥AG于M点，
∵∠HGC=45°，∠CMG=90°，∴△CMG是等腰直角三角形，
∴MG=CM，∵AE=BE=，∴CD=BC=AB=2，
由（1）知：△ADE≌△BAH，∴BH=AE=CH=，AH=DE，
∴AH=DE=，
∵S△ADE=AF•DE=AE•AD，∴×2=5AF，∴AF=2，
∵∠AFE=∠CMH=90°，∴∠AEF=∠AHB=∠CHM，∵AE=CH，
∴△AFE≌△CMH（AAS），∴CM=AF=2，∴CM=MG=2，∴CG=2．
型号
制造每套家具平均用时（天）
每套家具的利润（万元）
甲
0.5
乙
0.8