

2022-2023学年河南省新乡市高二下学期期末数学试题(含解析)
展开1.已知复数z=1+i,则zz=( )
A. −2iB. iC. −iD. 1−i
2.设全集U=R,集合M=xx>−1,N=x−2
3.函数fx=3x−3−x2⋅cs2x的部分图象大致为
( )
A. B.
C. D.
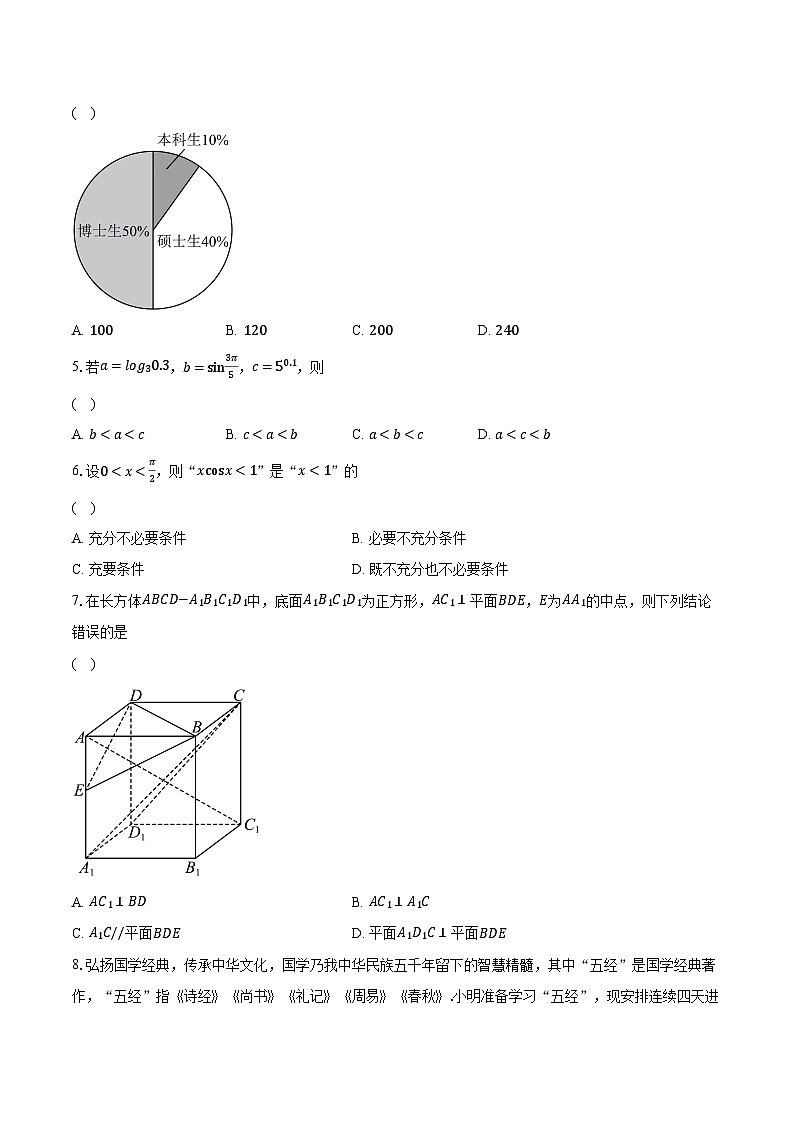
4.某高校现有400名教师,他们的学历情况如图所示,由于该高校今年学生人数急剧增长,所以今年计划招聘一批新教师,其中博士生80名,硕士生若干名,不再招聘本科生,且使得招聘后硕士生的比例下降了4%,招聘后全校教师举行植树活动,树苗共1500棵,若树苗均按学历的比例进行分配,则该高校本科生教师共分得树苗的棵数为
( )
A. 100B. 120C. 200D. 240
5.若a=lg30.3,b=sin3π5,c=50.1,则
( )
A. b
A. 充分不必要条件B. 必要不充分条件
C. 充要条件D. 既不充分也不必要条件
7.在长方体ABCD−A1B1C1D1中,底面A1B1C1D1为正方形,AC1⊥平面BDE,E为AA1的中点,则下列结论错误的是
( )
A. AC1⊥BDB. AC1⊥A1C
C. A1C//平面BDED. 平面A1D1C⊥平面BDE
8.弘扬国学经典,传承中华文化,国学乃我中华民族五千年留下的智慧精髓,其中“五经”是国学经典著作,“五经”指《诗经》《尚书》《礼记》《周易》《春秋》.小明准备学习“五经”,现安排连续四天进行学习且每天学习一种,每天学习的书都不一样,其中《诗经》与《礼记》不能安排在相邻两天学习,《周易》不能安排在第一天学习,则不同安排的方式有( )
A. 32种B. 48种C. 56种D. 68种
二、多选题:本题共4小题,共20分。在每小题给出的选项中,有多项符合题目要求。
9.已知直线l:4x+3y+6=0与圆C:(x−1)2+y2=9相交于E,F两点,则
( )
A. 圆心C到直线l的距离为1B. 圆心C到直线l的距离为2
C. EF= 5D. EF=2 5
10.已知函数f(x)=12sin2x−π6,下列说法正确的是
( )
A. f(x)的最小正周期为π2
B. f(x)的极值点为x=π3+kπ2(k∈Z)
C. f(x)的图象可由函数y=12sin2x的图象向右平移π12个单位长度得到
D. 若fx1=fx2,则x1=x2+kπ(k∈Z)
11.已知双曲线C:x2a2−y2b2=1(a>0,b>0)的右焦点F2( 3,0)到渐近线的距离为1 ,P 为C 上一点,下列说法正确的是
( )
A. C的离心率为 62
B. PF2的最小值为 22
C. 若A ,B 为C 的左、右顶点,P与A ,B 不重合,则直线PA,PB的斜率之积为12
D. 设C 的左焦点为F1,若△PF1F2的面积为 33,则∠F1PF2=2π3
12.若关于x的不等式xlnx+2−xln2−x≥m2−2m对任意x∈0,2恒成立,则整数m的取值可能为
( )
A. 1B. 2C. 3D. 4
三、填空题:本题共4小题,每小题5分,共20分。
13.已知向量a=(2,1),b=(1−m,m+1),若a→⊥b→,则m= .
14.已知csα−π3=12,则csπ3+2α= .
15.如图,某圆柱与圆锥共底等高,圆柱侧面的展开图恰好为正方形,则圆柱母线与圆锥母线所成角的正切值为 .
16.已知抛物线y2=4x上存在两点A,B(A,B异于坐标原点O),使得∠AOB=90∘,直线AB与x轴交于M点,将直线AB绕着M点逆时针旋转90∘与该抛物线交于C,D两点,则四边形ACBD面积的最小值为 .
四、解答题:本题共6小题,共70分。解答应写出文字说明,证明过程或演算步骤。
17.(本小题10分)
已知等差数列an满足2a2−a3=1,2a2+a3+2=a6.
(1)求an的通项公式;
(2)设bn=1an+3an+1+3,数列bn的前n项和为Tn,若Tm≤118,求m的最大值.
18.(本小题12分)
已知▵ABC的内角A,B,C所对的边分别是a,b,c,向量m=(a+b+c, 3b),n=(a+b−c,− 3a),且m→⊥n→.
(1)求角C的大小;
(2)若csB= 217,b=8,D为边BC上一点,且AD=7,若▵ABD,▵ACD的面积分别为S1,S2,求S1S2的值.
19.(本小题12分)
投壶是中国古代士大夫宴饮时做的一种投掷游戏,也是一种礼仪,在战国时期较为盛行,尤其是在唐朝,得到了发扬光大.投壶是把箭向壶里投,投中多的为胜.某校开展“健康体育节”活动,其间甲、乙两人轮流进行定点投壶比赛(每人各投一次为一轮,且不受先后顺序影响),在相同的条件下,甲、乙两人每轮在同一位置,每人投一次.若两人有一人投中,投中者得2分,未投中者得−2分;若两人都投中,两人均得1分;若两人都未投中,两人均得0分.设甲每次投中的概率为13,乙每次投中的概率为25,且各次投壶互不影响.
(1)用Pi表示经过第i轮投壶累计得分后甲得分等于乙得分的概率,求P1与P2;
(2)经过2轮投壶,记甲、乙的得分之和为X,求X的分布列和数学期望.
20.(本小题12分)
如图,四棱锥P−ABCD的底面是边长为2的菱形,▵PAD为等边三角形.
(1)若PC⊥AD,证明:AC=CD.
(2)在(1)条件下,若PC=3 ,求平面PAB与平面PAD夹角的余弦值.
21.(本小题12分)
已知椭圆E:x2a2+y2b2=1a>b>0的左、右焦点分别为F1、F2,离心率为12,且椭圆E上的点到焦点的距离的最大值为3.
(1)求椭圆E的方程.
(2)设A、B是椭圆E上关于x轴对称的不同两点,P在椭圆E上,且点P异于A、B两点,O为原点,直线AP交x轴于点M,直线BP交x轴于点N,试问OM⋅ON是否为定值?若为定值,求出这个定值;若不是定值,请说明理由.
22.(本小题12分)
已知函数f(x)=ax3+bx2+cx(a≠0),且6a+b=0,f(1)=4a.
(1)讨论f(x)的单调性;
(2)若x∈[0,3],函数F(x)=f(x)−xe−x有三个零点x1,x2,x3,且x1
1.【答案】C
【解析】【分析】
本题考查了复数的除法运算,共轭复数,属于基础题.
利用共轭复数的定义结合复数的除法可化简复数 zz .
【解答】
解:因为 z=1+i ,
则 zz=1−i1+i=(1−i)2(1+i)(1−i)=−2i2=−i .
故选:C.
2.【答案】B
【解析】【分析】
本题考查交并补混合运算,属于基础题.
根据集合的交并补运算即可结合选项逐一求解.
【解答】
解:由题意可得 M∩N=x−1
对于A, ∁UM∩N= xx≤−1 或 x≥3 ,故A错误,
对于B, ∁UM∪N= xx≤−2 ,故B正确,
对于C, M∩(∁UN)={x|x⩾3} ,故C错误,
对于D, N∪∁UM=xx<3 ,故D错误,
故选:B.
3.【答案】A
【解析】【分析】
本题考查函数图像的识别,特殊值法,属于基础题.
根据奇函数的定义判断函数 fx 为奇函数,排除B,C,求函数的零点,再根据函数值的正负排除D可得答案.
【解答】
解:函数 fx=3x−3−x2⋅cs2x 的定义域为 R ,定义域关于原点对称,
又 f−x=3−x−3x2⋅cs−2x=−3x−3−x2⋅cs2x =−f(x),
所以函数 fx 为奇函数,其图象关于原点对称,排除B,C;
令 fx=0 ,可得 3x−3−x2⋅cs2x=0 ,
所以 3x−3−x=0 或 cs2x=0 ,
所以 x=0 或 x=kπ2+π4 , k∈Z ,
当 0
故选:A.
4.【答案】B
【解析】【分析】
本题考查扇形图、属于基础题.
设招聘 x 名硕士生,然后根据题意结合扇形统计图列方程可求出 x 的值,再根据比例可求得结果.
【解答】
解:设招聘 x 名硕士生,由题意可知, x+400×0.4=(400+80+x)×(0.4−0.04) ,
解得 x=20 ,
所以本科生教师共分得树苗 40400+80+20×1500=120 棵.
故选:B
5.【答案】C
【解析】【分析】
本题考查指数函数的函数值、对数型函数的函数值、任意角的三角函数的定义,属于基础题.
由指数函数、对数函数、三角函数的性质可得 a<0 , b∈(0,1) , c>1 ,即可得答案.
【解答】
解:因为 a=lg30.3<0 , b=sin3π5∈(0,1) , c=50.1>1 ,所以 a
6.【答案】B
【解析】【分析】
本题考查了充分条件和必要条件,余弦函数的性质,属于基础题.
根据充分条件和必要条件的定义结合余弦函数的性质分析判断即可.
【解答】
解:设0
若 x<1 ,又 0
故选:B
7.【答案】D
【解析】【分析】
本题考查线面垂直的性质和判定,线面垂直的向量表示,线面平行的判定
由条件,结合线面垂直的性质判断A,连接 AC ,设 AC∩BD=O ,证明 EO//A1C ,由线面垂直定义证明 AC1⊥EO ,由此判断B,由线面平行判定定理证明 A1C// 平面 BDE ,判断C,建立空间直角坐标系,求平面 A1D1C ,平面 BDE 的法向量,判断两向量数量积是否为0,判断D.
【解答】
解:因为 AC1⊥ 平面 BDE , BD⊂ 平面 BDE ,所以 AC1⊥BD ,A正确;
连接 AC ,设 AC∩BD=O ,则 O 为 AC 的中点,
因为 AC1⊥ 平面 BDE , EO⊂ 平面 BDE ,所以 AC1⊥EO ,
又 E 为 AA1 的中点, O 为 AC 的中点,所以 EO//A1C ,
所以 AC1⊥A1C ,B正确;
因为 EO//A1C ,
又 EO⊂ 平面 BDE , A1C⊄ 平面 BDE ,所以 A1C //平面 BDE ,C正确;
由已知 D1A1,D1C1,D1D 两两垂直,以 D1 为原点, D1A1,D1C1,D1D 为 x,y,z 的正方向,建立空间直角坐标系,设 A1B1=2a ,
因为底面 A1B1C1D1 为正方形,所以 A1D1=2a,A1C1=2 2a ,
由长方体性质可得四边形 ACC1A1 为矩形,又 AC1⊥A1C ,
所以四边形 ACC1A1 为正方形,故 AA1=2 2a ,
所以 D10,0,0,A12a,0,0,C0,2a,2 2a,A2a,0,2 2a,C10,2a,0 ,
所以 AC1=−2a,2a,−2 2a,D1A1=2a,0,0,D1C=0,2a,2 2a ,
因为 AC1⊥ 平面 BDE ,所以 AC1=−2a,2a,−2 2a 为平面 BDE 的一个法向量,
设平面 A1D1C 的法向量为 n=x,y,z ,
则 n⋅D1A1=0n⋅D1C=0 ,所以 2ax=02ay+2 2az=0 ,
取 y= 2 ,则 x=0,z=−1 ,
所以 n=0, 2,−1 为平面 A1D1C 的一个法向量,
因为 n⋅AC1=2 2a+2 2a=4 2a≠0 ,
所以向量 n,AC1 不垂直,所以平面 A1D1C 与平面 BDE 不垂直,D错误;
故选:D.
8.【答案】D
【解析】【分析】
本题考查排列与组合的综合应用,分类加法计数原理,属于中档题.
利用排列组合分别讨论不排《周易》,排《周易》且《诗经》与《礼记》都安排,排《周易》且《诗经》与《礼记》只安排一个,三种情况,再利用分类加法计数原理将所有情况相加即可.
【解答】
解:①若《周易》不排,先将《诗经》与《礼记》以外的另外2种排列,
再将《诗经》与《礼记》插空,则共有 A22A32=12 种安排方式.
②若排《周易》且《诗经》与《礼记》都安排,
在《尚书》和《春秋》中先选1种,然后将《诗经》与《礼记》以外的另外2种排列,
再将《诗经》与《礼记》插空,减去将《周易》排在第一天的情况即可,
共有 C21A22A32−C21A22=20 种安排方式;
③若排《周易》且《诗经》与《礼记》只安排一个,
先在《诗经》与《礼记》中选1种,然后将《周易》排在后三天的一天,
最后将剩下的3种书全排列即可,
共有 C21C31A33=36 种安排方式.
所以共有 12+20+36=68 种安排方式.
故选:D.
9.【答案】BD
【解析】【分析】
本题考查直线与圆相交的弦长、点到直线的距离,属于基础题.
根据点到直线的距离公式计算可知A错误,B正确;利用几何法求出弦长可知C错误,D正确.
【解答】
解:因为圆心C(1,0)到直线l的距离d=4×1+3×0+6 42+32=2,所以 A错误,B正确.
因为|EF|=2 9−22=2 5,所以 C错误,D正确.
故选:BD.
10.【答案】BC
【解析】【分析】
本题考查正弦函数的周期性、图像变换、利用导数求已知函数的极值或极值点,属于中档题.由正弦函数的最小正周期的计算公式可判断A;对f(x)求导,令f′(x)=0可判断B;由三角函数的平移变换可判断C;由fx1=fx2,求出x1=x2+kπ(k∈Z)或x1=2π3−x2+kπ(k∈Z)可判断D.
【解答】
解:f(x) 的最小正周期为T=2π2=π,所以 A错误;
由f′(x)=cs2x−π6=0,得x=π3+kπ2(k∈Z),
由三角函数的性质可验证f(x)的极值点为x=π3+kπ2(k∈Z),所以 B正确;
将y=12sin2x的图象向右平移π12个单位长度得到f(x)=12sin2x−π6的图象,所以 C正确;
若fx1=fx2,则12sin2x1−π6=12sin2x2−π6,
所以sin2x1−π6=sin2x2−π6,则2x1−π6=2x2−π6+2kπ(k∈Z)或2x1−π6+2x2−π6=π+2kπ(k∈Z),
则x1=x2+kπ(k∈Z)或x1=2π3−x2+kπ(k∈Z),所以 D错误.
故选:BC.
11.【答案】ACD
【解析】【分析】
本题考查了双曲线的离心率,渐近线,焦点三角形,属于中档题.
根据题意列关于a,b,c的等式,从而可得双曲线的方程,计算离心率,PF2的最小值,结合动点P满足的方程x022−y02=1,列式计算kPA⋅kPB,在焦点三角形△PF1F2中,由双曲线的定义,余弦定理以及三角形面积公式列式即可计算出∠F1PF2.
【解答】
解:由已知可得c= 3,cb a2+b2=b=1,所以a= 2,
则C的方程为x22−y2=1,离心率为 3 2= 62, A正确;
因为PF2的最小值为c−a= 3− 2,所以 B错误;
设Px0,y0,则x022−y02=1,A− 2,0,B 2,0
kPA⋅kPB=y0x0+ 2⋅y0x0− 2=y02x02−2=x022−1x02−2=12,所以 C正确;
设∠F1PF2=θ,由PF1−PF2=2aF1F22=PF12+PF22−2PF1S▵PF1F2=12PF1PF2sinθPF2csθ,
可得S▵PF1F2=b2tanθ2=1tanθ2= 33,得tanθ2= 3,
则∠F1PF2=2π3,所以 D正确.
故选:ACD.
12.【答案】AB
【解析】【分析】
本题考查利用导数研究恒成立与存在性问题,属于中档题.
构造函数fx=xlnx+2−xln2−x,求导,利用导数求解函数的最值,进而将问题转为m2−2m≤fxmin,即可由一元二次不等式求解.
【解答】
解:令fx=xlnx+2−xln2−x,则f′(x)=ln x+1−ln (2−x)−1=ln x−ln (2−x),
由于函数y=lnx在x∈0,2单调递增,y=ln2−x在x∈0,2单调递减,
所以f′(x)=ln x−ln (2−x)在x∈0,2单调递增,
又f′1=0,所以当x∈0,1,f′x<0,fx单调递减,当x∈1,2,f′x>0,fx单调递增,
所以当x=1时,fx取极小值也是最小值,故fxmin=f1=0,
对于不等式xlnx+2−xln2−x≥m2−2m对任意x∈0,2恒成立,
则m2−2m≤fxmin⇒m2−2m≤0,所以0≤m≤2,
故整数m的取值可能为0,1,2,
故选:AB
13.【答案】3
【解析】【分析】
本题考查向量数量积的坐标表示与向量的垂直关系,属于基础题.
由向量垂直的坐标表示列方程求 m ,可得结论.
【解答】
解:因为 a⊥b , a=2,1 , b=1−m,m+1 ,
所以 2×1−m+1×m+1=0 ,
所以 2−2m+m+1=0 ,
所以 m=3 .
故答案为: 3 .
14.【答案】12
【解析】【分析】
本题考查二倍角余弦公式,属于基础题.
利用诱导公式和二倍角公式由条件求值.
【解答】
解:因为 cs (π3+2α)=cs [2(α−π3)+π]
=−cs 2(α−π3)=1−2cs2(α−π3) ,
又 csα−π3=12 ,
所以 csπ3+2α=1−2×14=12 .
故答案为:12.
15.【答案】12π
【解析】【分析】
本题考查了圆柱的结构特征,圆锥的结构特征,属于基础题.
先根据圆柱侧面展开图为正方形得出 2π⋅BO=OA ,然后根据题意找到圆柱母线与圆锥母线所成的角即可求得.
【解答】
解:因为圆柱母线与圆锥的轴平行,
所以圆柱母线与圆锥母线所成角的大小等于 ∠BAO .
因为圆柱侧面的展开图恰好为正方形,
所以 2π⋅BO=OA ,所以 tan∠BAO=BOOA=12π .
故答案为: 12π .
16.【答案】80
【解析】【分析】
本题考查抛物线中的面积问题,向量数量积的坐标表示与向量的垂直关系,由基本不等式求最值或取值范围.
设直线 AB 的方程为 x=my+t ,联立方程组,由条件证明 t=4 ,由此可得 AB ,再求 CD ,求四边形ACBD面积的解析式,求其最小值即可.
【解答】
解:由已知直线 AB 的斜率存在,且不为 0 ,
故可设直线 AB 的方程为 x=my+t ,m≠0,
联立 y2=4xx=my+t ,
消 x 得, y2−4my−4t=0 ,
方程 y2−4my−4t=0 的判别式 Δ=16m2+16t>0 ,
设 Ax1,y1,Bx2,y2 ,则 y1+y2=4m,y1y2=−4t ,
所以 x1x2=y124⋅y224=t2
因为 ∠AOB=90∘ ,
所以 OA⋅OB=0 ,所以 x1x2+y1y2=0 ,
所以 t2−4t=0 ,
又 A,B 异于坐标原点 O ,所以 y1y2≠0 ,所以 t≠0 ,
所以 t=4 ,
所以直线 AB 的方程为 x=my+4 ,
且 AB= 1+m2y2−y1= 1+m2 16m2+64=4 m2+1m2+4
所以直线 AB 与 x 轴的交点为 4,0 ,
所以点 M 的坐标为 4,0 ,
所以直线 CD 的方程为 x=−1my+4 ,
联立 y2=4xx=−1my+4 ,
消 x 得, y2+4my−16=0 ,
方程 y2+4my−16=0 的判别式 Δ=16m2+64>0 ,
设 Cx3,y3,Dx3,y4 ,则 y3+y4=−4m,y1y2=−16 ,
所以 CD= 1+1m2y4−y3= 1+1m2 16m2+64=4m2 m2+14m2+1 ,
由已知 AB⊥CD ,
所以四边形ACBD面积 S=12×AB×CD=8m2+1m2 m2+44m2+1 ,
设 m2=λ ,则 λ>0 , S=8 λ+124λ2+17λ+4λ2 ,
所以 S=8 λ2+1+2λ4λ2+4+17λλ2=8 4λ+1λ2+25λ+1λ+34 ,
由基本不等式可得 λ+1λ≥2 ,当且仅当 λ=1 时等号成立,此时 m=±1 ,
设 μ=λ+1λ ,可得 S=8 4μ2+25μ+34=8 4μ+2582−8116 , μ≥2 ,
所以当 μ=2 时,即 m=±1 时, S 取最小值,最小值为 80 ,
所以四边形ACBD面积的最小值为 80 .
故答案为: 80 .
17.【答案】解:(1)设公差和首项为 d,a1 ,
由 2a2−a3=1 , 2a2+a3+2=a6 得 2a1+d−a1+2d=12a1+d+a1+2d+2=a1+5d ,
解得 a1=1d=4 ,
所以 an=a1+4n−1=4n−3
(2)bn=1an+3an+1+3=14n−3+34n+1+3=1161n−1n+1 ,
因此 Tn=116×[(1−12)+(12−13)+(13−14)+⋯+(1n−1n+1)]=116(1−1n+1) ,
故 Tm≤118 ,则 Tm=1161−1m+1≤118 ,解得 m≤8 ,
故 m 的最大值为8
【解析】本题考查等差数列通项公式中的基本量计算、裂项相消法求和,属于中档题.
(1)根据等差数列基本量的计算即可求解首项和公差,
(2)根据裂项求和求解 Tn=1161−1n+1 ,即可解不等式求解.
18.【答案】解:(1)因为 m=a+b+c, 3b , n=a+b−c,− 3a , m⊥n ,
所以 a+b+c⋅a+b−c−3ab=0 ,
所以 a2+b2−c2=ab ,
所以 csC=a2+b2−c22ab=12 ,又 C∈0,π ,
所以 C=π3 ;
(2)因为 B∈0,π , csB= 217>0 ,所以 B∈0,π2 ,
所以 sinB= 1−cs2B=2 77 ,
sinA=sin(B+C) =sin(B+π3) =sinBcsπ3+csBsinπ3 ,
=2 77×12+ 217× 32 =5 714 ,
在 ▵ABC 中,由正弦定理得 asinA=bsinB ,
所以 a=8×5 7142 77=10 ,
在 ▵ACD 中,由余弦定理得: AD2=DC2+AC2−2DC⋅ACcsC ,
即 DC2−8DC+15=0 ,
故 (DC−3)(DC−5)=0 ,
所以 DC=3 或 DC=5 ,
当 DC=5 时, BD=BC−DC=5 ,
S1S2=12×DA×DB×sin∠ADB12×DA×DC×sin∠ADC=BDDC=1 ,
当 DC=3 时, BD=BC−DC=7 ,
S1S2=12×DA×DB×sin∠ADB12×DA×DC×sin∠ADC=BDDC=73 ,
所以 S1S2 的值为 73 或1.
【解析】本题考查三角形面积公式、利用正弦定理解三角形、利用余弦定理解三角形,属于中档题.(1)由条件,根据向量垂直的坐标表示可得 a,b,c 的关系,再结合余弦定理求角C的大小;
(2)根据 csB= 217 ,得到进而得到 sinB , sinA ,然后由正弦定理求得a,再利用余弦定理和三角形面积公式求解.
19.【答案】解:(1)由题意可知, P1=13×25+23×35=815 ,
P2=C2113×1−25×1−13×25+8152=88225 .
(2)由题意可知,随机变量 X 的可能取值有 0 、 2 、 4 ,
PX=4=13×252=4225 ,
PX=2=C21×13×25×23×35+C21×13×35×13×25+C21×13×25×23×25=52225 ,
PX=0=1−52225−4225=169225 ,
所以,随机变量 X 的分布列如下表所示:
因此, EX=0×169225+2×52225+4×4225=815 .
【解析】本题考查离散型随机变量的均值、分布列、相互独立事件的概率乘法公式,属于中档题.
(1)根据独立事件的概率乘法公式结合互斥事件的概率加法公式可求得 P1 、 P2 的值;
(2)分析可知随机变量 X 的可能取值有 0 、 2 、 4 ,计算出随机变量 X 在不同取值下的概率,可得出随机变量 X 的分布列,进而可求得 EX 的值.
20.【答案】解:(1)证明:取 AD 的中点 O ,连接 OP , OC .
因为 ▵PAD 为等边三角形,所以 PO⊥AD .
又 PC⊥AD , PO∩PC=P , PO,PC⊂ 平面 POC ,
所以 AD⊥ 平面 PCO ,因为 CO⊂ 平面 POC ,
所以 AD⊥CO ,即 OC 是线段 AD 的中垂线,
所以 AC=CD .
(2)由(1)知AD⊥ 平面 PCO ,AD⊥OC,AC=CD=2 ,
以 O 为坐标原点,OC,OD所在直线分别为x轴,y轴,在平面PCO内过O作OC的垂线为z轴,建立空间直角坐标系,
则 A(0,−1,0) , C( 3,0,0) , D(0,1,0) .
在 ▵POC 中, PO=OC= 3 , PC=3 ,由余弦定理易得∠POC为120°,
所以点 P 的坐标为 − 32,0,32 ,
所以 AB=DC=( 3,−1,0) , AP=− 32,1,32 , AD=(0,2,0) .
设 n=(x,y,z) 是平面 PAB 的法向量,可得 3x−y=0,− 32x+y+32z=0, 令 y=3 ,得 n=( 3,3,−1) .
设 m=x1,y1,z1 是平面 PAD 的法向量,可得 2y1=0,− 32x1+y1+32z1=0, 令 z1=1 ,得 m=( 3,0,1) .
设平面 PAB 与平面 PAD的夹角为 θ ,
则 cs θ=|n⋅m||n||m|= 1313 .
【解析】本题考查平面与平面夹角的向量求法,线面垂直的判定与性质,属于中档题.
(1)根据等边三角形的三线合一性质,结合线面垂直的判定定理以及性质定理,可得答案;
(2)根据题意,建立空间直角坐标系,求得两平面的法向量,结合夹角的求解公式,可得答案.
21.【答案】解:(1)设点 Px0,y0 为椭圆 E 上任意一点,其中 −a≤x0≤a ,易知点 F1−c,0 ,
PF1= x0+c2+y02= x02+2cx0+c2+b2−b2x02a2= a2+2cx0+c2x02a2
=a+cax0=a+cax0∈a−c,a+c ,
所以,椭圆 E 上的点到焦点的距离的最大值为 a+c=3 ,
又因为椭圆 E 的离心率为 e=ca=12 ,
所以, a=2 , c=1 ,则 b= a2−c2= 4−1= 3 ,
因此,椭圆 E 的标准方程为 x24+y23=1 .
(2)设点 Ax1,y1 , Bx1,−y1 , Px2,y2 , Mm,0 , Nn,0 ,
则直线 AP 的方程为 y=y1x1−mx−m ,直线 BP 的方程为 y=−y1x1−nx−n ,
联立 y=y1x1−mx−m3x2+4y2=12 ,消去 y 并整理可得 3x12−6mx1+3m2+4y12x2−8my12x+4m2y12−12x1−m2=0 ,
因为点 A 在椭圆 E 上,则直线 AP 与椭圆 E 必有公共点,
所以, x1+x2=8my123x12−6mx1+3m2+4y12 ,
同理可得 x1+x2=8ny123x12−6nx1+3n2+4y12
所以, 8my123x12−6mx1+3m2+4y12=8ny123x12−6nx1+3n2+4y12 ,
所以, m3x12−6nx1+3n2+4y12=n3x12−6mx1+3m2+4y12 ,
化简可得 3m−nx12+4m−ny12=3mnm−n ,
当 m≠n 时,则 3mn=3x12+4y12=12 ,此时, mn=4 ;
当 m=n 时, M 、 N 、 P 三点重合,此时, m=n=a=2 .
综上所述, OM⋅ON=mn=4 ,即 OM⋅ON 为定值 4 .
【解析】本题考查椭圆中的定值问题,属于较难题.
(1)求出椭圆 E 上任意一点到其焦点距离的最大值,结合离心率可得出 a 、 c 的值,进而求出 b 的值,由此可得出椭圆 E 的标准方程;
(2)设点 Ax1,y1 , Bx1,−y1 , Px2,y2 , Mm,0 , Nn,0 ,将直线 AP 的方程与椭圆 E 的方程联立,求出 x1+x2 ,同理可得出 x1+x2 的另外一个表达式,利用等量关系可得出关于 m 、 n 的等式,讨论 m≠n 、 m=n 两种情形,可求出 OM⋅ON 的定值.
22.【答案】解:(1)由 f(1)=4a ,得 3a−b−c=0 ,又 b=−6a ,所以 c=9a ,
则 f(x)=ax3−6ax2+9ax ,所以 f′(x)=3a(x−1)(x−3) , a≠0 .
当 a>0 时,令 f′(x)>0 ,得 x<1 或 x>3 ;令 f′x<0 ,得 1
当 a<0 时,令 f′(x)>0 ,得 1
所以 f(x) 在 (−∞,1) 与 (3,+∞) 上单调递减,在 (1,3) 上单调递增.
(2)x1+x2+x3<2 ,理由如下:
因为 f(x)=ax3−6ax2+9ax=ax(x−3)2 ,
由 F(x)=0 ,得 ax(x−3)2−xe−x=0 ,解得 x=0 或 a(x−3)2−e−x=0 .
因为 x∈[0,3] ,所以 x1=0 , x2 , x3 是 a(x−3)2−e−x=0 的正根,则 x1+x2+x3=x2+x3 ,
又 lnax−32=lne−x=−x ,
所以 lna+2ln3−x2=−x2 , lna+2ln3−x3=−x3 ,
两式相减得 2ln3−x2−2ln3−x3=x3−x2=3−x2−3−x3 .
令 3−x2=t2 , 3−x3=t3 ,则 3>t2>t3≥0 ,得 2lnt2−2lnt3=t2−t3 ,则 2=t2−t3lnt2−lnt3 .
令 u=t2t3∈(1,+∞) ,则 t2−t3lnt2−lnt3=t3(u−1)lnu=2 ,
所以 t3=2ln uu−1(u>1) , t2=ut3=2ulnuu−1 ,可得 t2+t3=2(u+1)lnuu−1 ,
t2+t3−4=2lnuu−1(u+1)−4=2(u+1)lnu−4(u−1)u−1(u>1) .
设 g(u)=2(u+1)lnu−4(u−1) ,则 g′(u)=2lnu+1u−1 ,
再设 h(u)=lnu+1u−1u>1 ,则 h′(u)=1u−1u2=u−1u2>0 ,
所以 h(u) 在 (1,+∞) 上为增函数,则 h(u)>h(1)=0 ,
即 g′(u)=2lnu+1u−1>0 ,则 g(u)=2(u+1)lnu−4(u−1) 在 (1,+∞) 上为增函数,
从而 g(u)>g(1)=2(1+1)ln1−4(1−1)=0 ,
所以 t2+t3−4>0 ,即 3−x2+3−x3−4=2−x2+x3>0 ,
所以 x2+x3<2 ,即 x1+x2+x3=x2+x3<2 .
【解析】本题考查利用导数研究函数的零点、利用导数求函数的单调区间,属于困难题.
(1)分类讨论 a>0 与 a<0 ,结合导数与函数的关系即可得解;
(2)观察式子先确定 x1=0 ,再利用转化法与换元法得到 2lnt2−2lnt3=t2−t3 ,进而利用双变量处理方法得到 t2+t3−4=2(u+1)lnu−4(u−1)u−1 ,利用导数证得 t2+t3−4>0 ,从而得解.
X
0
2
4
P
169225
52225
4225
2023-2024学年河南省新乡市高二上学期1月期末测试数学试题(含解析): 这是一份2023-2024学年河南省新乡市高二上学期1月期末测试数学试题(含解析),共17页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。
2022-2023学年河南省商丘名校高二下学期期末联考数学试题(含解析): 这是一份2022-2023学年河南省商丘名校高二下学期期末联考数学试题(含解析),共16页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。
2022-2023学年河南省漯河市高二下学期期末数学试题(含解析): 这是一份2022-2023学年河南省漯河市高二下学期期末数学试题(含解析),共20页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。












