山东省济南高新区四校联考2023-2024学年数学八上期末复习检测模拟试题含答案

这是一份山东省济南高新区四校联考2023-2024学年数学八上期末复习检测模拟试题含答案，共7页。试卷主要包含了考生必须保证答题卡的整洁，化简式子的结果为，等腰三角形的两边长分别是，等内容，欢迎下载使用。

学校_______ 年级_______ 姓名_______
考生请注意：
1．答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内，不得在试卷上作任何标记。
2．第一部分选择题每小题选出答案后，需将答案写在试卷指定的括号内，第二部分非选择题答案写在试卷题目指定的位置上。
3．考生必须保证答题卡的整洁。考试结束后，请将本试卷和答题卡一并交回。
一、选择题（每题4分，共48分）
1．如图，在同一直线上，≌，，，则的值为（ ）
A．B．C．D．
2．甲乙两地相距420千米,新修的高速公路开通后,在甲、乙两地行驶的长途客运车平均速度是原来的1.5倍,进而从甲地到乙地的时间缩短了2小时．设原来的平均速度为x千米/时,可列方程为（ ）
A．B．
C．D．
3．下列图形中，是中心对称图形的是（ ）
A．B．C．D．
4．若一个三角形的两边长分别为3和7，则第三边长可能是( )
A．6B．3C．2D．11
5．校乒乓球队员的年龄分布如下表所示：
对于不同的，下列关于年龄的统计量不会发生改变的是（ ）
A．众数，中位数B．众数，方差C．平均数，中位数D．平均数，方差
6．如图，长方形纸片ABCD中，点E是AD的中点，且AE＝1，BE的垂直平分线MN恰好过C．则长方形的一边CD的长度为（ ）
A．1B．C．D．2
7．把分式分子、分母中的，同时扩大为原来的2倍，那么该分式的值（ ）
A．扩大为原来的2倍B．缩小为原来的2倍
C．不变D．扩大为原来的4倍
8．化简式子的结果为（ ）
A．B．C．D．
9．某公司有学徒工和熟练工两个工种的工人，已知一个学徒工每天制造的零件比一个熟练少个，一个学徒工与两个熟练工每天共可制造个零件，求一个学徒工与 一个熟练工每天各能制造多少个零件?设一个学徒工每天能制造个零件，一个熟练工每天能制造个零件，根据题意可列方程组为( )
A．B．
C．D．
10．等腰三角形的两边长分别是，．则它的周长是( )
A．B．C．或D．
11．下列命题是真命题的是（ ）
A．在一个三角形中，至多有两个内角是钝角
B．三角形的两边之和小于第三边
C．在一个三角形中，至多有两个内角是锐角
D．在同一平面内，垂直于同一直线的两直线平行
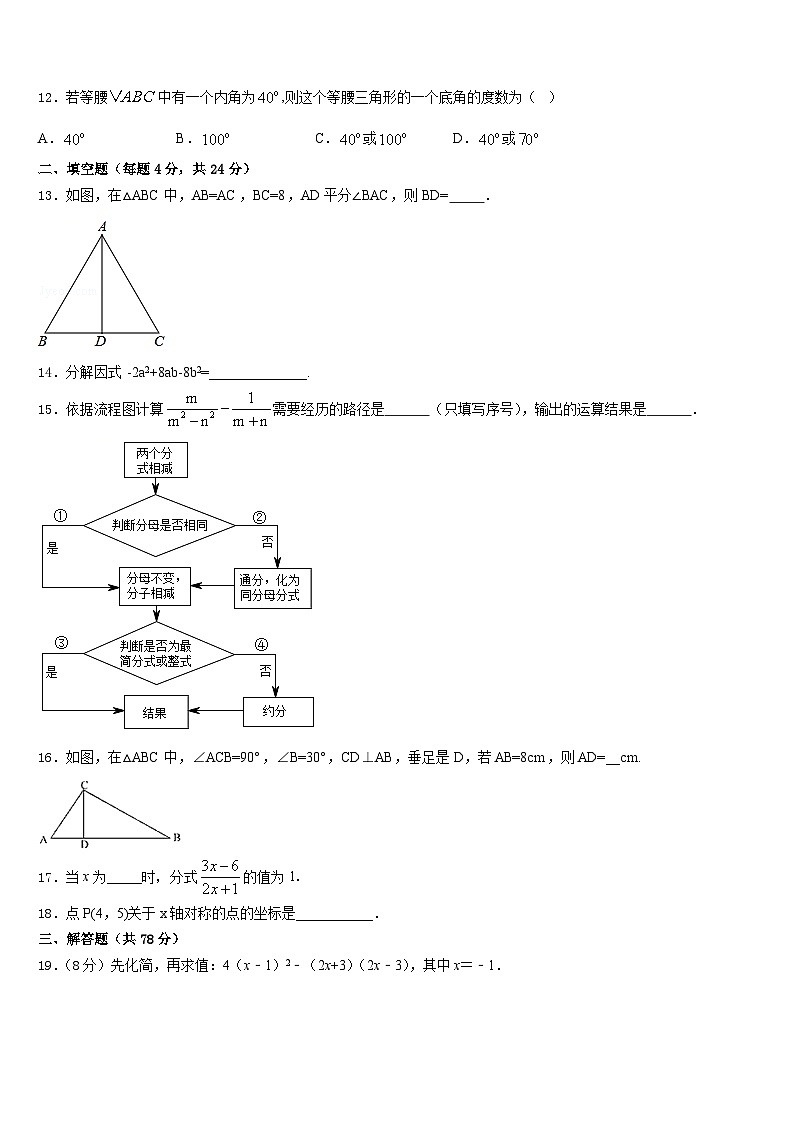
12．若等腰中有一个内角为,则这个等腰三角形的一个底角的度数为（ ）
A．B．C．或D．或
二、填空题（每题4分，共24分）
13．如图，在△ABC中，AB=AC，BC=8，AD平分∠BAC，则BD= ．
14．分解因式 -2a2+8ab-8b2=______________.
15．依据流程图计算需要经历的路径是 （只填写序号），输出的运算结果是 ．
16．如图，在△ABC中，∠ACB=90°，∠B=30°，CD⊥AB，垂足是D，若AB=8cm，则AD=__cm.
17．当x为_____时，分式的值为1．
18．点P(4，5)关于x轴对称的点的坐标是___________．
三、解答题（共78分）
19．（8分）先化简，再求值：4（x﹣1）2﹣（2x+3）（2x﹣3），其中x＝﹣1．
20．（8分）如图，已知在△ABC中，AB＝AC，D是BC边上任意一点，E在AC边上，且AD＝AE．
（1）若∠BAD＝40°，求∠EDC的度数；
（2）若∠EDC＝15°，求∠BAD的度数；
（3）根据上述两小题的答案，试探索∠EDC与∠BAD的关系．
21．（8分）已知矩形ABCD的一条边AD=8，E是BC边上的一点，将矩形ABCD沿折痕AE折叠，使得顶点B落在CD边上的点P处，PC=4（如图1）．
（1）求AB的长；
（2）擦去折痕AE，连结PB，设M是线段PA的一个动点（点M与点P、A不重合）．N是AB沿长线上的一个动点，并且满足PM=BN．过点M作MH⊥PB，垂足为H，连结MN交PB于点F（如图2）．
①若M是PA的中点，求MH的长；
②试问当点M、N在移动过程中，线段FH的长度是否发生变化？若变化，说明理由；若不变，求出线段FH的长度．
22．（10分）计算
（1）
（2）
（3）
（4）
23．（10分）全社会对空气污染问题越来越重视，空气净化器的销量也大增，商社电器从厂家购进了，两种型号的空气净化器，已知一台型空气净化器的进价比一台型空气净化器的进价多300元，用7500元购进型空气净化器和用6000元购进型空气净化器的台数相同．
（1）求一台型空气净化器和一台型空气净化器的进价各为多少元？
（2）在销售过程中，型空气净化器因为净化能力强，噪声小而更受消费者的欢迎．商社电器计划型净化器的进货量不少于20台且是型净化器进货量的三倍，在总进货款不超过5万元的前提下，试问有多少种进货方案？
24．（10分）如图1，张老师在黑板上画出了一个，其中，让同学们进行探究．
（1）探究一：
如图2，小明以为边在内部作等边，连接，请直接写出的度数_____________；
（2）探究二：
如图3，小彬在（1）的条件下，又以为边作等边，连接.判断与的数量关系；并说明理由；
（3）探究三：
如图3，小聪在（2）的条件下，连接，若，求的长．
25．（12分）如图，在中，是的平分线，于，于，试猜想与之间有什么关系？并证明你的猜想．
26．（12分）化简求值：
（1）已知，求的值．
（2）已知，求代数式的值．
参考答案
一、选择题（每题4分，共48分）
1、C
2、B
3、C
4、A
5、A
6、C
7、A
8、D
9、A
10、A
11、D
12、D
二、填空题（每题4分，共24分）
13、1
14、-2(a-2b)2
15、②③，．
16、2
17、2
18、 (4，-5）
三、解答题（共78分）
19、化简结果：-8x+13，值为21.
20、（1）20°；（2）30°；（3）∠EDC＝∠BAD，见解析
21、 (1)1；（2）；.
22、（1）；（2）；（3）；（4）
23、 (1)每B型空气净化器、每台A型空气净化器的进价分别为1200元，1500元；(2)有两种方案：购B型空气净化器为7台，A型净化器为21台；购B型空气净化器为8台，A型净化器为24台.
24、（1）150；（2）CE=AD．理由见解析；（3）．
25、详见解析
26、 (1)3;(2)-11
年龄（岁）
人数