2022-2023学年湖南省长沙市天心区明德中学高二（上）期末数学试卷

这是一份2022-2023学年湖南省长沙市天心区明德中学高二（上）期末数学试卷，共21页。试卷主要包含了单项选择题，多项选择题，填空题，解答题等内容，欢迎下载使用。

1．（5分）已知集合A＝{﹣1，0，1，2，3}，B＝{x|﹣1＜x＜2}，则A∩B＝（ ）
A．{﹣1，0}B．{﹣1，0，1}C．{0，1}D．{0，1，2}
2．（5分）若，则z﹣|z|2＝（ ）
A．B．C．D．
3．（5分）圆心为（1，﹣2），且与x轴相切的圆的标准方程为（ ）
A．（x﹣1）2+（y+2）2＝2B．（x﹣1）2+（y+2）2＝4
C．（x+1）2+（y﹣2）2＝2D．（x+1）2+（y﹣2）2＝4
4．（5分）在公比为负数的等比数列{an}中，a1+a2＝﹣1，a7＝256a3，则a3+2a4+a5＝（ ）
A．48B．﹣48C．80
5．（5分）函数f（x）＝ex（sinx+csx）在点（0，1）处切线方程为（ ）
A．y＝4x+1B．y＝3x+1C．y＝2x+1D．y＝x+1
6．（5分）已知椭圆的左、右焦点分别为F1，F2，过坐标原点的直线交E于P，Q两点，且PF2⊥F2Q，且，则E的标准方程为（ ）
A．B．
C．D．
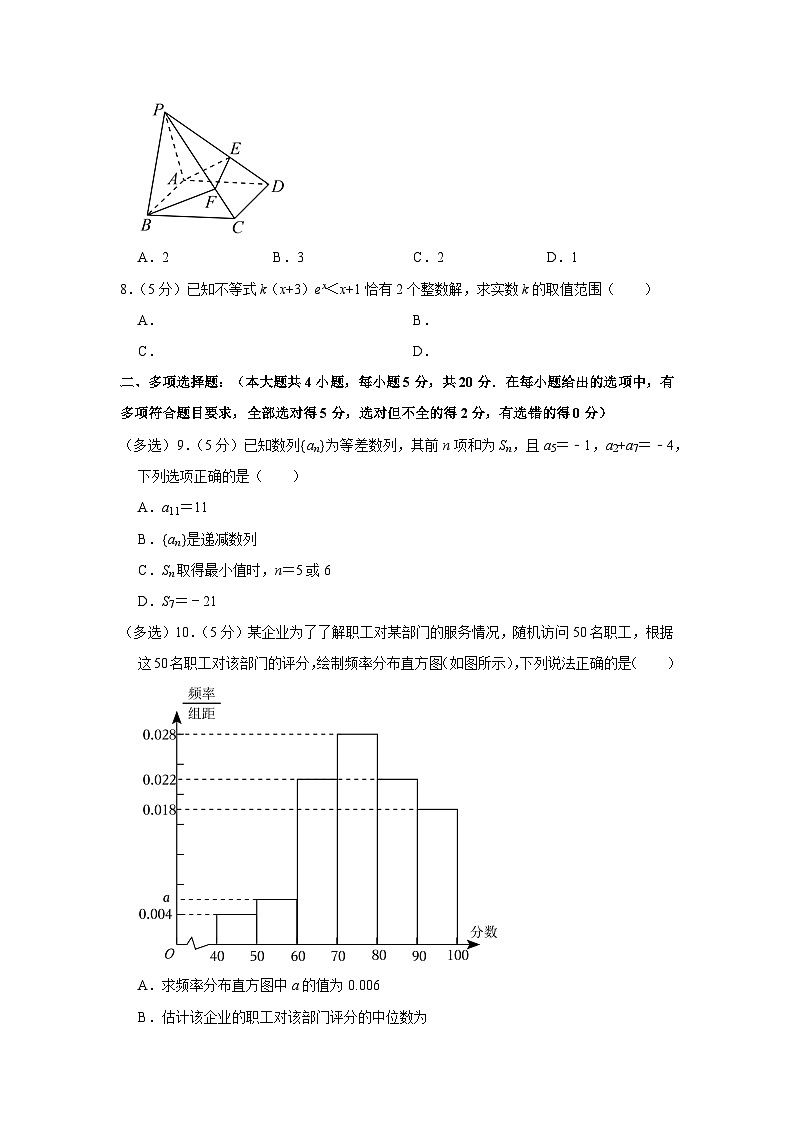
7．（5分）如图，在四棱锥P﹣ABCD中，平面PAB⊥平面ABCD，底面ABCD是正方形，△PAB是边长为2的正三角形，E，F分别是棱PD，PC上的动点，则AE+EF+BF的最小值是（ ）
A．2B．3C．2D．1
8．（5分）已知不等式k（x+3）ex＜x+1恰有2个整数解，求实数k的取值范围（ ）
A．B．
C．D．
二、多项选择题：（本大题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符合题目要求，全部选对得5分，选对但不全的得2分，有选错的得0分）
（多选）9．（5分）已知数列{an}为等差数列，其前n项和为Sn，且a5＝﹣1，a2+a7＝﹣4，下列选项正确的是（ ）
A．a11＝11
B．{an}是递减数列
C．Sn取得最小值时，n＝5或6
D．S7＝﹣21
（多选）10．（5分）某企业为了了解职工对某部门的服务情况，随机访问50名职工，根据这50名职工对该部门的评分，绘制频率分布直方图（如图所示），下列说法正确的是（ ）
A．求频率分布直方图中a的值为0.006
B．估计该企业的职工对该部门评分的中位数为
C．估计该企业的职工对该部门评分的平均值为76.5
D．从评分在[40，60）的受访职工中，随机抽取2人，求此2人评分都在[40，50）的概率为
（多选）11．（5分）已知函数f（x）＝x3﹣3ax+2的极值点分别为x1，x2（x1＜x2），则下列选项正确的是（ ）
A．a＞0
B．f（x1）+f（x2）＝2
C．若f（x2）＜0，则a＞1
D．过（0，2）仅能做曲线y＝f（x）的一条切线
（多选）12．（5分）已知F是抛物线C：y2＝4x的焦点，O为坐标原点，A，B是抛物线C上的两点，AB的中点M在C的准线上的投影为N，则（ ）
A．曲线C的准线方程为x＝﹣2
B．若|AF|＝4，则△AOF的面积为
C．若OA⊥OB，则|OA|•|OB|≥32
D．若∠AFB＝60°，则|MN|≤|AB|
三、填空题：本大题共4小题，每小题5分，共20分，请把答案直接填写在答题卡相应位置上．
13．（5分）已知函数f（x），则f（2）＝ ．
14．（5分）函数f（x）＝cs2x+3csx的最大值为 ．
15．（5分）已知双曲线C：1（a＞0，b＞0）的渐近线与圆x2+y2﹣2x0相切，则双曲线C的离心率为 ．
16．（5分）颇受青年朋友喜欢的蛋白石六角锥灵摆吊坠如图（1）所示，现在我们通过手工制作一个六角锥吊坠模型．准备一张圆形纸片，已知圆心为O，半径为10cm，该纸片上的正六边形ABCDEF的中心为O，A1，B1，C1，D1，E1，F1为圆O上的点，如图（2）所示．△A1AB，△B1BC，△C1CD，△D1DE，△E1EF，△F1FA分别是以AB，BC，CD，DE，EF，FA为底边的等腰三角形．沿虚线剪开后，分别以AB，BC，CD，DE，EF，FA为折痕折起△A1AB，△B1BC，△C1CD，△D1DE，△E1EF，△F1FA，使A1，B1，C1，D1，E1，F1重合，得到六棱锥，当底面六边形的边长变化时，所得六棱锥体积的最大值为 cm3．
四、解答题：本大题共6小题，共70分，请把答案填写在答题卡相应位置上．
17．（10分）已知数列{an}满足a1＝1，an+1＝2an+1（n∈N*）．
（1）证明：数列{an+1}是等比数列；
（2）设bn＝lg2（an+1），求数列的前n项和Tn．
18．（12分）进行垃圾分类收集可以减少垃圾处理量和处理设备，降低处理成本，减少土地资源的消耗，具有社会、经济、生态等多方面的效益，是关乎生态文明建设全局的大事．为了普及垃圾分类知识，某学校举行了垃圾分类知识考试，试卷中只有两道题目，已知甲同学答对每题的概率都为，乙同学答对每题的概率都为p，且在考试中每人各题答题结果互不影响．已知每题甲、乙两位同学中恰有一人答对的概率为．
（1）求p的值及每题甲、乙两位同学同时答对的概率；
（2）试求两人答对的题数之和为3的概率．
19．（12分）如图所示，在四棱锥P﹣ABCD中，BC∥AD，∠BAD＝90°，AP＝AB＝AD＝3BC＝3，且PA⊥平面ABCD．
（1）证明：平面PBC⊥平面PAB；
（2）求平面PAB与平面PCD夹角的余弦值．
20．（12分）△ABC的内角A，B，C的对边分别为a，b，c已知sinAcsA＝0，a＝2，b＝2．
（1）求角A和边长c；
（2）设D为BC边上一点，且AD⊥AC，求△ABD的面积．
21．（12分）已知椭圆C：的左、右顶点分别为A、B，上顶点M与左右顶点连线MA，MB的斜率乘积为，焦距为4．
（1）求椭圆C的方程；
（2）设点P为椭圆上异于A，B的点，直线AP与y轴的交点为Q，过坐标原点O作ON∥AP交椭圆于N点，试探究是否为定值，若是，求出该定值；若不是，请说明理由．
22．（12分）已知函数和函数有相同的最大值，直线y＝m与两曲线y＝f（x）和y＝g（x）恰好有三个交点，从左到右三个交点横坐标依次为x1，x2，x3．
（1）求实数a的值；
（2）求证：x1x3．
2022-2023学年湖南省长沙市天心区明德中学高二（上）期末数学试卷
参考答案与试题解析
一、单项选择题：本大题共8小题，每小题5分，共40分，请把答案直接填涂在答题卡相应位置上.
1．（5分）已知集合A＝{﹣1，0，1，2，3}，B＝{x|﹣1＜x＜2}，则A∩B＝（ ）
A．{﹣1，0}B．{﹣1，0，1}C．{0，1}D．{0，1，2}
【分析】根据已知条件，结合交集的定义，即可求解．
【解答】解：集合A＝{﹣1，0，1，2，3}，B＝{x|﹣1＜x＜2}，
则A∩B＝{0，1}．
故选：C．
【点评】本题主要考查交集及其运算，属于基础题．
2．（5分）若，则z﹣|z|2＝（ ）
A．B．C．D．
【分析】根据已知条件，结合复数的四则运算，以及复数模公式，即可求解．
【解答】解：因为|z|，
所以．
故选：D．
【点评】本题主要考查复数的四则运算，以及复数模公式，属于基础题．
3．（5分）圆心为（1，﹣2），且与x轴相切的圆的标准方程为（ ）
A．（x﹣1）2+（y+2）2＝2B．（x﹣1）2+（y+2）2＝4
C．（x+1）2+（y﹣2）2＝2D．（x+1）2+（y﹣2）2＝4
【分析】由题意求出圆的半径，从而求得圆的标准方程．
【解答】解：圆心为（1，﹣2），且与x轴相切的圆的半径为2，
故圆的标准方程为（x﹣1）2+（y+2）2＝4，
故选：B．
【点评】本题主要考查求圆的标准方程，关键是求出圆的半径，属于基础题．
4．（5分）在公比为负数的等比数列{an}中，a1+a2＝﹣1，a7＝256a3，则a3+2a4+a5＝（ ）
A．48B．﹣48C．80
【分析】由已知结合等比数列的通项公式及性质可求首项及公比，然后结合等比数列的通项公式可求．
【解答】解：在公比为负数的等比数列{an}中，a1+a2＝a1（1+q）＝﹣1，
因为a7＝256a3，
所以q4256，
因为q＜0，
所以q＝﹣4，a1，
则a3+2a4+a5＝a1（q2+2q3+q4）＝48．
故选：A．
【点评】本题主要考查了等比数列的通项公式及等比数列的性质，属于基础题．
5．（5分）函数f（x）＝ex（sinx+csx）在点（0，1）处切线方程为（ ）
A．y＝4x+1B．y＝3x+1C．y＝2x+1D．y＝x+1
【分析】先求导，再求出f'（0），再利用点斜式可得切线方程．
【解答】解：由已知f'（x）＝ex（csx﹣sinx）+ex（sinx+csx）＝2csxex，
∴f'（0）＝2cs0e0＝2，
∴函数f（x）＝ex（sinx+csx）在点（0，1）处切线方程为y﹣1＝2（x﹣0），
即y＝2x+1．
故选：C．
【点评】本题主要考查了导数的几何意义在切线求解中的应用，属于基础题．
6．（5分）已知椭圆的左、右焦点分别为F1，F2，过坐标原点的直线交E于P，Q两点，且PF2⊥F2Q，且，则E的标准方程为（ ）
A．B．
C．D．
【分析】连接PF1，QF1，由椭圆的对称性得四边形PF1QF2为平行四边形，根据|PF2|+|F2Q|＝4，得2a＝4，由三角形面积解得PF2，QF2，计算F1F2即2c，求出b2可得椭圆的标准方程．
【解答】解：如图，连接PF1，QF1，由椭圆的对称性得四边形PF1QF2为平行四边形，
所以|PF2|+|F2Q|＝|PF2|+|PF1|＝2a＝4，得a＝2．
又因为PF2⊥F2Q，所以四边形PF1QF2为矩形，设|PF2|＝m，|QF2|＝n，
则，所以，得m＝n＝2，
则，则，b2＝a2﹣c2＝2，
椭圆的标准方程为．
故选：A．
【点评】本题主要考查椭圆的标准方程，直线与椭圆的综合，考查运算求解能力，属于中档题．
7．（5分）如图，在四棱锥P﹣ABCD中，平面PAB⊥平面ABCD，底面ABCD是正方形，△PAB是边长为2的正三角形，E，F分别是棱PD，PC上的动点，则AE+EF+BF的最小值是（ ）
A．2B．3C．2D．1
【分析】将平面PAD，PCD，PBC展开到一个平面内，则AE+EF+BF的最小值即为展开图中AB的长，利用余弦定理求解即可．
【解答】解：∵平面PAB⊥平面ABCD，平面PAB∩平面ABCD＝AB，AD⊂平面ABCD，AD⊥AB，
∴AD⊥平面PAB，又PA⊂平面PAB，
∴AD⊥PA，同理可得BC⊥PB．
由题意可知PA＝PB＝AB＝BC＝CD＝AD＝2，则，∠APD＝∠BPC＝45°．
将平面PAD，PCD，PBC展开到一个平面内如图，则AE+EF+BF的最小值即为展开图中AB的长．
∵，
从而，故．
在△PAB中，由余弦定理可得，
则，即AE+EF+BF的最小值为．
故选：D．
【点评】本题考查立体几何中距离的最值问题，考查余弦定理的运用，考查运算求解能力，属于中档题．
8．（5分）已知不等式k（x+3）ex＜x+1恰有2个整数解，求实数k的取值范围（ ）
A．B．
C．D．
【分析】原不等式k（x+3）ex＜x+1等价于，设g（x）＝k（x+3），，然后转化为函数的交点结合图象可求．
【解答】解：原不等式k（x+3）ex＜x+1等价于，
设g（x）＝k（x+3），，所以，得x＝0．
当x＜0时，f'（x）＞0，所以f（x）在（﹣∞，0）上单调递增，当x＞0时，f'（x）＜0，所以f（x）在（0，+∞）上单调递减，当x＝0时，f（x）取极大值．
又f（﹣1）＝0，且x＞0时，f（x）＞0，因此g（x）＝k（x+3）与的图象如下，直线g（x）＝k（x+3）恒过点（﹣3，0）．
当k≤0时，显然不满足条件；
当k＞0时，只需要满足，即，解得．
故选：D．
【点评】本题主要考查函数的零点与方程根的关系，考查数形结合思想与运算求解能力，属于中档题．
二、多项选择题：（本大题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符合题目要求，全部选对得5分，选对但不全的得2分，有选错的得0分）
（多选）9．（5分）已知数列{an}为等差数列，其前n项和为Sn，且a5＝﹣1，a2+a7＝﹣4，下列选项正确的是（ ）
A．a11＝11
B．{an}是递减数列
C．Sn取得最小值时，n＝5或6
D．S7＝﹣21
【分析】根据等差数列基本量法求出数列首项和公差，代入选项判断即可．
【解答】解：不妨设an＝a1+（n﹣1）da2+a7＝a1+d+a1+6d＝2a1+7d＝﹣4，与a5＝a1+4d＝﹣1联立，解得d＝2，a1＝﹣9，即通项an＝2n﹣11，
对于选项A．a11＝2×11﹣11＝11，故A正确；
对于选项B．d＞0，{an}是递增数列，故B错误；
对于选项C．Sn存在最小值，且有两个最小值，即S6﹣S5＝0，即a6＝0，与an不符，故C错误；
对于选项D．S7＝7a4＝7×（﹣3）＝﹣21，故正确．
故选：AD．
【点评】本题主要考查等差数列的前n项和公式，属于基础题．
（多选）10．（5分）某企业为了了解职工对某部门的服务情况，随机访问50名职工，根据这50名职工对该部门的评分，绘制频率分布直方图（如图所示），下列说法正确的是（ ）
A．求频率分布直方图中a的值为0.006
B．估计该企业的职工对该部门评分的中位数为
C．估计该企业的职工对该部门评分的平均值为76.5
D．从评分在[40，60）的受访职工中，随机抽取2人，求此2人评分都在[40，50）的概率为
【分析】结合频率分布直方图的性质，对选项进行逐项分析验证，即可解出．
【解答】解：选项A，由图可知，（0.004+a+0.022+0.028+0.022+0.018）×10＝1，所以a＝0.006，故A正确；
选项B，中位数为：70，故B正确；
选项C，平均值为：（45×0.004+55×0.006+65×0.022+75×0.028+85×0.022+95×0.018）×10＝76.2，故C错误；
选项D，评分在[40，60）职工有（0.004+0.006）×10×50＝5人，评分在[40，50）职工有0.004×10×50＝2人，故概率为：，故D正确；
故选：ABD．
【点评】本题考查了古典概型的概率，学生的数学运算能力，属于基础题．
（多选）11．（5分）已知函数f（x）＝x3﹣3ax+2的极值点分别为x1，x2（x1＜x2），则下列选项正确的是（ ）
A．a＞0
B．f（x1）+f（x2）＝2
C．若f（x2）＜0，则a＞1
D．过（0，2）仅能做曲线y＝f（x）的一条切线
【分析】首先根据已知条件得到，，再结合导数的性质依次判断选项即可．
【解答】解：∵f（x）＝x3﹣3ax+2，∴f'（x）＝3x2﹣3a，
又函数f（x）＝x3﹣3ax+2的极值点分别为x1，x2（x1＜x2），
∴3x2﹣3a＝0有两个不相等的实数根x1，x2（x1＜x2），
∴a＞0，故A正确．
对选项B，∵a＞0，∴，
∴，f'（x）＞0，f（x）为增函数；
，f'（x）＜0，f（x）为减函数；
，f'（x）＞0，f（x）为增函数，
∴，为函数f（x）的极值点，
∴，故B错误．
对选项C，∵，
化简得，∴a＞1，故C正确；
对选项D，设切点为，又f'（x）＝3x2﹣3a，切线过（0，2），
∴，即，解得x0＝0，
∴过（0，2）仅能做曲线y＝f（x）的一条切线，故D正确．
故选：ACD．
【点评】本题考查利用导数研究函数的极值点，利用导数求曲线的切线问题，方程思想，化归转化思想，属中档题．
（多选）12．（5分）已知F是抛物线C：y2＝4x的焦点，O为坐标原点，A，B是抛物线C上的两点，AB的中点M在C的准线上的投影为N，则（ ）
A．曲线C的准线方程为x＝﹣2
B．若|AF|＝4，则△AOF的面积为
C．若OA⊥OB，则|OA|•|OB|≥32
D．若∠AFB＝60°，则|MN|≤|AB|
【分析】根据抛物线的标准方程，求出准线方程判断A；求出点A的纵坐标计算判断B；设出点A，B的坐标，结合向量垂直的坐标表示及均值不等式求解判断C；利用抛物线定义结合余弦定理、均值不等式推理判断D作答．
【解答】解：∵抛物线C方程为：y2＝4x，
∴抛物线的焦点F（1，0），准线l：x＝﹣1，
设A（x1，y1），B（x2，y2），
则，，y1≠y2，
对A选项，∵曲线C的准线方程为x＝﹣1，∴A选项错误；
对B选项，∵|AF|＝x1+1＝4，∴x1＝3，∴，
∴△AOF的面积，∴B选项正确；
对C选项，∵OA⊥OB，
∴，显然y1y2≠0，
∴y1y2＝﹣16，x1x2＝16，
∴
，
当且仅当x1＝x2＝4时取等号，∴C选项正确；
对D选项，设点M的横坐标为x0，∴x1+x2＝2x0，
∴|AF|+|BF|＝x1+1+x2+1＝2（x0+1）＝2|MN|，
在△AFB中，∵∠AFB＝60°，
∴由余弦定理得|AB|2＝|AF|2+|BF|2﹣2|AF|⋅|BF|cs∠AFB，
∵，
∴，
当且仅当|AF|＝|BF|时取等号，
∴|MN|≤|AB|，∴D选项正确．
故选：BCD．
【点评】本题考查抛物线的几何性质，化归转化思想，基本不等式的应用，属中档题．
三、填空题：本大题共4小题，每小题5分，共20分，请把答案直接填写在答题卡相应位置上．
13．（5分）已知函数f（x），则f（2）＝ 0 ．
【分析】直接代入分段函数中求值即可．
【解答】解：当x＞1时，f（x）＝ln（x﹣1）
所以f（2）＝ln（2﹣1）＝ln1＝0，
故答案为：0．
【点评】本题考查分段函数的知识，属于基础题．
14．（5分）函数f（x）＝cs2x+3csx的最大值为 4 ．
【分析】先用余弦的二倍角展开，把函数转化为关于csx的二次函数求解即可．
【解答】解：因为f（x）＝cs2x+3csx＝2cs2x﹣1+3csx＝2cs2x+3csx﹣1，
由﹣1≤csx≤1，
所以当csx＝1时，．
故答案为：4．
【点评】本题主要考查了三角函数的图象和性质，属于基础题．
15．（5分）已知双曲线C：1（a＞0，b＞0）的渐近线与圆x2+y2﹣2x0相切，则双曲线C的离心率为 ．
【分析】结合已知条件，写出双曲线的渐近线方程，然后利用圆心到直线的距离等于半径求出a，b，c之间的关系即可求解．
【解答】解：不妨取双曲线（a＞0，b＞0）的一条渐近线方程为，即bx﹣ay＝0，
又圆的方程可化为，
∴圆心坐标为（1，0），半径为，
由题意可得，即，
即b2＝2a2，即，
又a2+b2＝c2，
∴双曲线的离心率为，
故答案为：．
【点评】本题考查双曲线的几何性质，方程思想，化归转化思想，属中档题．
16．（5分）颇受青年朋友喜欢的蛋白石六角锥灵摆吊坠如图（1）所示，现在我们通过手工制作一个六角锥吊坠模型．准备一张圆形纸片，已知圆心为O，半径为10cm，该纸片上的正六边形ABCDEF的中心为O，A1，B1，C1，D1，E1，F1为圆O上的点，如图（2）所示．△A1AB，△B1BC，△C1CD，△D1DE，△E1EF，△F1FA分别是以AB，BC，CD，DE，EF，FA为底边的等腰三角形．沿虚线剪开后，分别以AB，BC，CD，DE，EF，FA为折痕折起△A1AB，△B1BC，△C1CD，△D1DE，△E1EF，△F1FA，使A1，B1，C1，D1，E1，F1重合，得到六棱锥，当底面六边形的边长变化时，所得六棱锥体积的最大值为 cm3．
【分析】连接OE1，交EF于点H，由题意得OE1⊥EF，设EF＝2xcm，则cm，cm，由已知求出，利用条件得六棱锥的体积，转化为函数，利用函数导数求解即可．
【解答】解：连接OE1，交EF于点H，由题意得OE1⊥EF，
设EF＝2xcm，则cm，cm
因为，所以，
∴六棱锥的高cm．
∴正六边形ABCDEF的面积cm2，
则六棱锥的体积cm3．
令函数，
则，
当时，f'（x）＞0，当时，f'（x）＜0，
所以f（x）在上单调递增，在上单调递减，
所以cm3．
故答案为：．
【点评】本题考查六棱锥体积的最值的求解，函数思想，导数研究函数单调性，属中档题．
四、解答题：本大题共6小题，共70分，请把答案填写在答题卡相应位置上．
17．（10分）已知数列{an}满足a1＝1，an+1＝2an+1（n∈N*）．
（1）证明：数列{an+1}是等比数列；
（2）设bn＝lg2（an+1），求数列的前n项和Tn．
【分析】（1）利用等比数列的定义变形为an+1+1＝2（an+1），即可证明结论；
（2）由（1）得数列{an+1}是首项为2，公比为2的等比数列，则，即，可得bn＝n，利用裂项相消法求和，即可得出答案．
【解答】解：（1）证明：∵an+1＝2an+1，
∴an+1+1＝2（an+1），即，
又a1+1＝2，
故数列{an+1}是首项为2，公比为2的等比数列；
（2）由（1）得数列{an+1}是首项为2，公比为2的等比数列，则，即，
∴bn＝lg2（an+1）＝n，
∴，
故．
【点评】本题考查数列求和和等比数列的定义，考查转化思想，考查逻辑推理能力和运算能力，属于中档题．
18．（12分）进行垃圾分类收集可以减少垃圾处理量和处理设备，降低处理成本，减少土地资源的消耗，具有社会、经济、生态等多方面的效益，是关乎生态文明建设全局的大事．为了普及垃圾分类知识，某学校举行了垃圾分类知识考试，试卷中只有两道题目，已知甲同学答对每题的概率都为，乙同学答对每题的概率都为p，且在考试中每人各题答题结果互不影响．已知每题甲、乙两位同学中恰有一人答对的概率为．
（1）求p的值及每题甲、乙两位同学同时答对的概率；
（2）试求两人答对的题数之和为3的概率．
【分析】（1）由互斥事件和对立事件的概率公式列方程可解得p，再求解每题甲、乙两位同学同时答对的概率；
（2）分别求出两人答对1道的概率，答对两道题的概率，两人共答对3道题，则是一人答对2道题另一人答对1道题，由互斥事件和独立事件概率公式可得结论．
【解答】解：（1）设A＝{甲同学答对第一题}，B＝{乙同学答对第一题}，则，P（B）＝p．
设D＝{甲、乙二人中恰有一人答对第一题}，
C＝{甲、乙二人均答对第一题}，则C＝AB，．
由于二人答题互不影响，且每人各题答题结果互不影响，所以A与B相互独立，与相互互斥，
所以P（C）＝P（AB）＝P（A）P（B），．
由题意可得，则，，所以，
每题甲、乙同时答对的概率为；
（2）设Ai＝{甲同学答对了i道题}，Bi＝{乙同学答对了i道题}，i＝0，1，2．
由题意得，，，，．
设E＝{甲乙二人共答对3道题}，则E＝A1B2+A2B1.由于Ai和Bi相互独立，A1B2与A2B1相互互斥，
所以．
所以，甲乙二人共答对3道题的概率为．
【点评】本题考查相互独立事件的概率计算，属于中档题．
19．（12分）如图所示，在四棱锥P﹣ABCD中，BC∥AD，∠BAD＝90°，AP＝AB＝AD＝3BC＝3，且PA⊥平面ABCD．
（1）证明：平面PBC⊥平面PAB；
（2）求平面PAB与平面PCD夹角的余弦值．
【分析】（1）根据条件证明PA⊥BC，AB⊥BC，再由线面垂直的判定定理得到BC⊥平面PAB，进一步证明面面垂直；
（2）以A为原点，以AB，AD，AP所在直线分别为x，y，z轴，建立空间直角坐标系，求出平面PCD的法向量和平面PAB的法向量，再求出平面PAB与平面PCD夹角的余弦值．
【解答】解：（1）证明：∵PA⊥平面ABCD，BC⊂平面ABCD，
∴PA⊥BC，
∵BC∥AD，∠BAD＝90°，∴AB⊥BC，
∵PA∩AB＝A，PA，AB⊂平面PAB，
∴BC⊥平面PAB，又BC⊂平面PBC，
∴平面PBC⊥平面PAB．
（2）由（1）易知AB，AD，AP两两垂直，
以A为原点，以AB，AD，AP所在直线分别为x，y，z轴，建立空间直角坐标系，
如下图所示：
则P（0，0，3），C（3，1，0），D（0，3，0），
∴，
设平面PCD的法向量为，
则，取y＝3，得，
易知平面PAB的一个法向量为，
∴，
∴平面PAB与平面PCD夹角的余弦值为．
【点评】本题主要考查二面角的平面角，属于中档题．
20．（12分）△ABC的内角A，B，C的对边分别为a，b，c已知sinAcsA＝0，a＝2，b＝2．
（1）求角A和边长c；
（2）设D为BC边上一点，且AD⊥AC，求△ABD的面积．
【分析】（1）先根据同角的三角函数的关系求出A，再根据余弦定理即可求出，
（2）先根据夹角求出csC，求出CD的长，得到S△ABDS△ABC．
【解答】解：（1）∵sinAcsA＝0，
∴tanA，
∵0＜A＜π，
∴A，
由余弦定理可得a2＝b2+c2﹣2bccsA，
即28＝4+c2﹣2×2c×（），
即c2+2c﹣24＝0，
解得c＝﹣6（舍去）或c＝4，
故c＝4．……（5分）
（2）∵c2＝b2+a2﹣2abcsC，
∴16＝28+4﹣2×22×csC，
∴csC，
∴CD，
∴CDBC，
∵S△ABCAB•AC•sin∠BAC4×22，
∴S△ABDS△ABC．…（10分）
【点评】本题考查了余弦定理和三角形的面积公式，以及解三角形的问题，考查了转化思想和数形结合思想的应用，属于中档题．
21．（12分）已知椭圆C：的左、右顶点分别为A、B，上顶点M与左右顶点连线MA，MB的斜率乘积为，焦距为4．
（1）求椭圆C的方程；
（2）设点P为椭圆上异于A，B的点，直线AP与y轴的交点为Q，过坐标原点O作ON∥AP交椭圆于N点，试探究是否为定值，若是，求出该定值；若不是，请说明理由．
【分析】（1）设P（x0，y0），kAP•kBP•可得，进而由2c＝4，可求椭圆C的方程；
（2）设直线PA的方程为y＝k（x+4），（k≠0），则Q（0，4k），联立方程组可求P的坐标，进而可得，，可求值．
【解答】解：（1）设P（x0，y0），即1，
∴kAP•kBP•，
又2c＝4，∴c＝2，
∴a2﹣b2＝4，解得a＝4，b＝2，
∴椭圆C的方程为1；
（2）设直线PA的方程为y＝k（x+4），（k≠0），则Q（0，4k），
∴直线OM的方程为y＝kx，联立直线直线AP所椭圆的方程，
可得（3+4k2）x2+32k2x﹣64k2﹣48＝0，
由xA＝﹣4，可得xP，
联立直线OM与椭圆C的方程可得，
（3+4k2）x2﹣48＝0，即，
2．
∴是定值，定值为2．
【点评】本题考查求椭圆的标准方程，考查求定值问题，考查运算求解能力，属中档题．
22．（12分）已知函数和函数有相同的最大值，直线y＝m与两曲线y＝f（x）和y＝g（x）恰好有三个交点，从左到右三个交点横坐标依次为x1，x2，x3．
（1）求实数a的值；
（2）求证：x1x3．
【分析】（1）分别对f（x），g（x）求导，得出f（x），g（x）的单调性，求出f（x），g（x）的最大值，即可求出实数a的值；
（2）画出f（x），g（x）的图象，设f（x），g（x）图象的交点为M，直线y＝m经过点M时，此时直线y＝m与两曲线y＝f（x）和y＝g（x）恰好有三个交点，可得0＜x1＜1＜x2＜e＜x3，再利用指对同构及f（x）的单调性，即可证明．
【解答】解：（1），，
当a＜0时，x＞1时，f'（x）＞0，f（x）单调递增，x＜1时，f'（x）＜0，f（x）单调递减，
所以当x＝1时，函数f（x）有最小值，没有最大值，不符合题意；
当a＞0时，当x＞1时，f'（x）＜0，f（x）单调递减，当x＜1时，f'（x）＞0，f（x）单调递增，
所以当x＝1时，函数f（x）有最大值，
即；
当a＞0时，当x＞e时，g'（x）＜0，g（x）单调递减，
当0＜x＜e时，g'（x）＞0，g（x）单调递增，
所以当x＝e时，函数g（x）有最大值，即；
于是有，
∵a＞0，
∴a＝1；
证明：（2）两个函数大致图象如下：设f（x），g（x）图象的交点为M，
当直线y＝m经过点M时，此时直线y＝m与两曲线y＝f（x）和y＝g（x）恰好有三个交点，
不妨设0＜x1＜1＜x2＜e＜x3，且（*），
由，又x1＜1，lnx2＜lne＝1，
又当x＜1时，f（x）单调递增，所以x1＝lnx2，又，又x2＞1，lnx3＞lne＝1，
又当x＞1时，f（x）单调递减，所以x2＝lnx3，由（*）可得：，，
于是有，即．
【点评】本题主要考查了导数与单调性关系的应用，还考查了导数与单调性及函数性质在等式证明中的应用，属于中档题．
声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布日期：2023/12/8 10:27:41；用户：18086013149；邮箱：18086013149；学号：27613231