

2023-2024学年河北省沧州市献县八年级数学第一学期期末调研试题含答案
展开学校_______ 年级_______ 姓名_______
注意事项
1.考生要认真填写考场号和座位序号。
2.试题所有答案必须填涂或书写在答题卡上,在试卷上作答无效。第一部分必须用2B 铅笔作答;第二部分必须用黑色字迹的签字笔作答。
3.考试结束后,考生须将试卷和答题卡放在桌面上,待监考员收回。
一、选择题(每题4分,共48分)
1.已知方程组的解是,则的值为( )
A.1B.2C.3D.0
2.现有纸片:4张边长为的正方形,3张边长为的正方形(),8张宽为,长为的长方形,用这15张纸片重新拼出一个长方形,那么该长方形较长的边长为( )
A.B.C.D.
3.已知等腰三角形的两边长分别为3和6,则它的周长等于( )
A.12B.12或15C.15D.15或18
4.下列函数关系中,随的增大而减小的是( )
A.长方形的长一定时,其面积与宽的函数关系
B.高速公路上匀速行驶的汽车,其行驶的路程与行驶时间的函数关系
C.如图1,在平面直角坐标系中,点、,的面积与点的横坐标的函数关系
D.如图2,我市某一天的气温(度)与时间(时)的函数关系
5.下列代数运算正确的是( )
A.B.C.D.
6.对于函数y=-3x+1,下列说法不正确的是( )
A.它的图象必经过点(1,-2)B.它的图象经过第一、二、四象限
C.当x> 时,y>0D.它的图象与直线y=-3x平行
7.我们知道,平面内不垂直的两条相交直线是轴对称图形,该图形对称轴条数为( )
A.1B.2C.4D.无数
8.若数据5,-3,0,x,4,6的中位数为4,则其众数为( )
A.4B.0C.-3D.4、5
9.从边长为的大正方形纸板中挖去一个边长为的小正方形纸板后,将其裁成四个相同的等腰梯形(如图甲),然后拼成一个平行四边形(如图乙).那么通过计算两个图形阴影部分的面积,可以验证成立的公式为( )
A.B.
C.D.
10.如图,给正五边形的顶点依次编号为1,2,3,4,1.若从某一顶点开始,沿正五边形的边顺时针方向行走,顶点编号的数字是几,就走几个边长,则称这种走法为一次“移位”,如:小宇在编号为3的顶点上时,那么他应走3个边长,即从3→4→1→1为第一次“移位”,这时他到达编号为1的顶点,然后从1→2为第二次“移位”.若小宇从编号为4的顶点开始,第2020次“移位”后,则他所处顶点的编号为( ).
A.2B.3C.4D.1
11.若分式等于零,则的值是( )
A.B.C.D.
12.下列计算正确的是( )
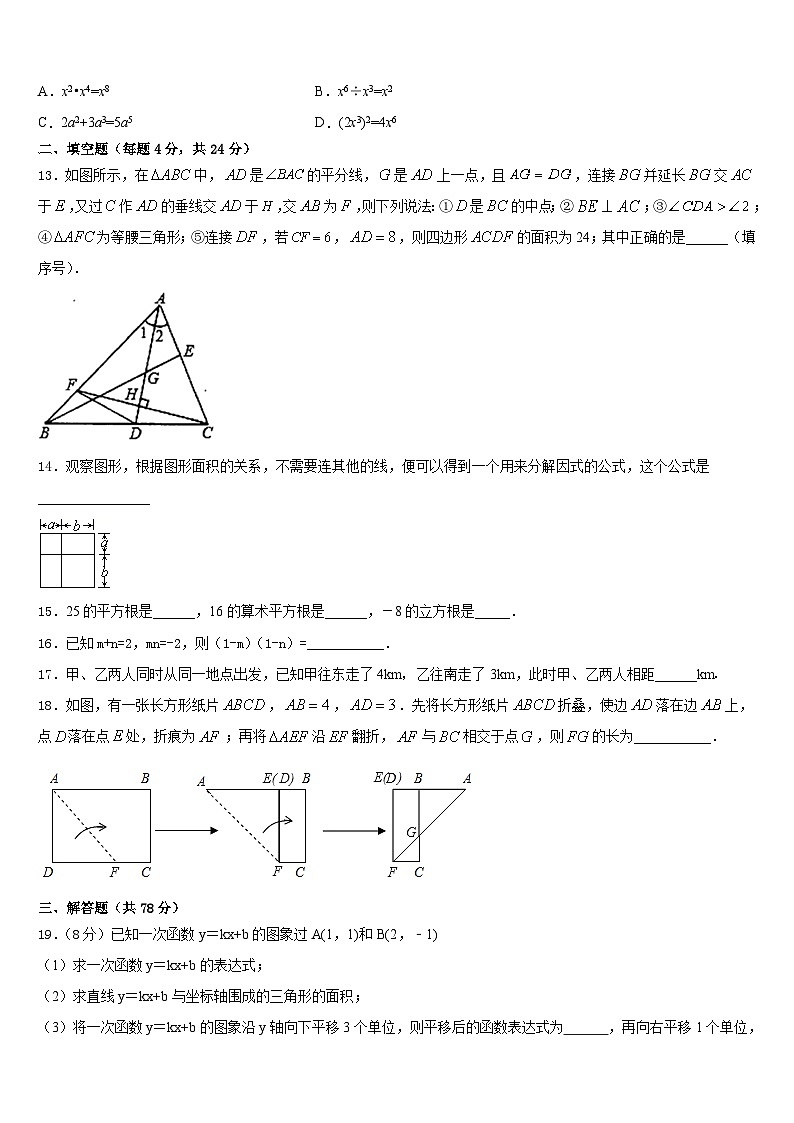
A.x2•x4=x8B.x6÷x3=x2
C.2a2+3a3=5a5D.(2x3)2=4x6
二、填空题(每题4分,共24分)
13.如图所示,在中,是的平分线,是上一点,且,连接并延长交于,又过作的垂线交于,交为,则下列说法:①是的中点;②;③;④为等腰三角形;⑤连接,若,,则四边形的面积为24;其中正确的是______(填序号).
14.观察图形,根据图形面积的关系,不需要连其他的线,便可以得到一个用来分解因式的公式,这个公式是________________
15.25的平方根是______,16的算术平方根是______,-8的立方根是_____.
16.已知m+n=2,mn=-2,则(1-m)(1-n)=___________.
17.甲、乙两人同时从同一地点出发,已知甲往东走了4km,乙往南走了3km,此时甲、乙两人相距______km.
18.如图,有一张长方形纸片,,.先将长方形纸片折叠,使边落在边上,点落在点处,折痕为;再将沿翻折,与相交于点,则的长为___________.
三、解答题(共78分)
19.(8分)已知一次函数y=kx+b的图象过A(1,1)和B(2,﹣1)
(1)求一次函数y=kx+b的表达式;
(2)求直线y=kx+b与坐标轴围成的三角形的面积;
(3)将一次函数y=kx+b的图象沿y轴向下平移3个单位,则平移后的函数表达式为 ,再向右平移1个单位,则平移后的函数表达式为 .
20.(8分)已知函数y=,且当x=1时y=2;
请对该函数及其图象进行如下探究:
(1)根据给定的条件,可以确定出该函数的解析式为 ;
(2)根据解折式,求出如表的m,n的值;
m= ,n= .
(3)根据表中数据.在如图所示的平面直角坐标系中描点并画出函数图象;
(4)写出函数图象一条性质 ;
(5)请根据函数图象写出当>x+1时,x的取值范围.
21.(8分)已知,,,试解答下列问题:
(1)如图①,则__________,则与的位置关系为__________
(2)如图②,若点E、F在线段上,且始终保持,.则的度数等于__________;
(3)在第(2)题的条件下,若平行移动到图③所示
①在移动的过程中,与的数量关系是否发生改变,若不改变,求出它们之间的数量关系;若改变,请说明理由.
②当时,求的度数.
22.(10分)甲、乙两名队员参加设计训练,成绩分别被制成下列两个统计图:
根据以上信息,整理分析数据如下:
(1)表格中 , , ;
(2)分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩,若选派其中一名参赛,你认为应选哪名队员?
(3)如果乙再射击次,命中环,那么乙的射击成绩的方差 .(填“变大”“变小”或“不变”)
23.(10分)如图,在中,,,点是边上的动点(点与点、 不重合),过点作交射线于点 ,联结,点是的中点,过点 、作直线,交于点,联结、.
(1)当点在边上,设, .
①写出关于 的函数关系式及定义域;
②判断的形状,并给出证明;
(2)如果,求的长.
24.(10分)计算.
(1) (2).
25.(12分)分解因式:.
26.(12分)已知△ABC中,AB=17,AC=10,BC边上得高AD=8,则边BC的长为________
参考答案
一、选择题(每题4分,共48分)
1、C
2、A
3、C
4、C
5、C
6、C
7、B
8、A
9、A
10、C
11、C
12、D
二、填空题(每题4分,共24分)
13、③④⑤
14、
15、 4 -1
16、﹣3
17、5
18、
三、解答题(共78分)
19、(1)y=﹣1x+3;(1);(3)y=﹣1x,y=﹣1x+1
20、(1)y=;(2),2;(3)见解析;(4)当x<3时,y随x的增大而减小,当x>3时,y随x的增大而增大;(5)x<1.
21、(1)71°,平行;(1)36°;(3)①∠OCB=∠OFB;②∠OCA=54°.
22、(1)7;7.5;7(2)乙,理由见解析;(3)变小.
23、(1)①;②详见解析;(2)或
24、(1);(2)1
25、
26、21或1
x
…
﹣1
0
1
2
3
4
5
6
7
…
y
…
3
2.5
2
1.5
0
m
n
2.5
3
…
平均数(环)
中位数(环)
众数(环)
方差
甲
乙
河北省沧州市献县2023-2024学年八年级上学期期末数学试题(含答案): 这是一份河北省沧州市献县2023-2024学年八年级上学期期末数学试题(含答案),共20页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
2023-2024学年河北省沧州市献县数学九年级第一学期期末学业质量监测模拟试题含答案: 这是一份2023-2024学年河北省沧州市献县数学九年级第一学期期末学业质量监测模拟试题含答案,共8页。试卷主要包含了考生要认真填写考场号和座位序号等内容,欢迎下载使用。
2023-2024学年河北省献县数学九上期末调研模拟试题含答案: 这是一份2023-2024学年河北省献县数学九上期末调研模拟试题含答案,共8页。试卷主要包含了已知,则下列比例式成立的是等内容,欢迎下载使用。












