——度河北省正定县2023-2024学年八上数学期末综合测试试题含答案

这是一份——度河北省正定县2023-2024学年八上数学期末综合测试试题含答案，共8页。试卷主要包含了考生要认真填写考场号和座位序号，下列结论中，错误的有，下列线段长能构成三角形的是等内容，欢迎下载使用。

学校_______ 年级_______ 姓名_______
注意事项
1．考生要认真填写考场号和座位序号。
2．试题所有答案必须填涂或书写在答题卡上，在试卷上作答无效。第一部分必须用2B 铅笔作答；第二部分必须用黑色字迹的签字笔作答。
3．考试结束后，考生须将试卷和答题卡放在桌面上，待监考员收回。
一、选择题(每小题3分,共30分)
1．老大爷背了一背鸡鸭到市场出售，单价是每只鸡100元，每只鸭80元，他出售完收入了660元，那么这背鸡鸭只数可能的方案有（ ）
A．4种B．3种C．2种D．1种
2．如图，在△ABC中，∠C=90°，AD平分∠BAC，DE⊥AB于E，下列结论：①CD=ED；②AC+BE=AB；③∠BDE=∠BAC；④BE=DE；⑤SBDE：S△ACD=BD：AC，其中正确的个数（ ）
A．5个B．4个C．3个D．2个
3．下列关于分式方程增根的说法正确的是（ ）
A．使所有的分母的值都为零的解是增根
B．分式方程的解为零就是增根
C．使分子的值为零的解就是增根
D．使最简公分母的值为零的解是增根
4．A，B两地相距80km，甲、乙两人骑车分别从A，B两地同时相向而行，他们都保持匀速行驶．如图，l1，l2分别表示甲、乙两人离B地的距离y（km）与骑车时间x（h）的函数关系．根据图象得出的下列结论，正确的个数是（ ）
①甲骑车速度为30km/小时，乙的速度为20km/小时；
②l1的函数表达式为y=80﹣30x；
③l2的函数表达式为y=20x；
④小时后两人相遇．
A．1个B．2个C．3个D．4个
5．下列结论中，错误的有( )
①在Rt△ABC中，已知两边长分别为3和4，则第三边的长为5；
②△ABC的三边长分别为AB，BC，AC，若BC2+AC2＝AB2，则∠A＝90°；
③在△ABC中，若∠A：∠B：∠C＝1：5：6，则△ABC是直角三角形；
④若三角形的三边长之比为3：4：5，则该三角形是直角三角形；
A．0个B．1个C．2个D．3个
6．如图，正方形ABCD的边长为4，点E在对角线BD上，且∠DAE＝67.5°，EF⊥AB，垂足为F，则EF的长为（ ）
A．1B．C．4-2D．3-4
7．下列选项中，可以用来说明命题“若，则”属于假命题的反例是（ ）
A．，B．，
C．，D．，
8．已知点和在一次函数的图象上，则与的大小关系是（ ）
A．B．C．D．
9．下列线段长能构成三角形的是（ ）
A．3、4、7B．2、3、6C．5、6、11D．4、7、10
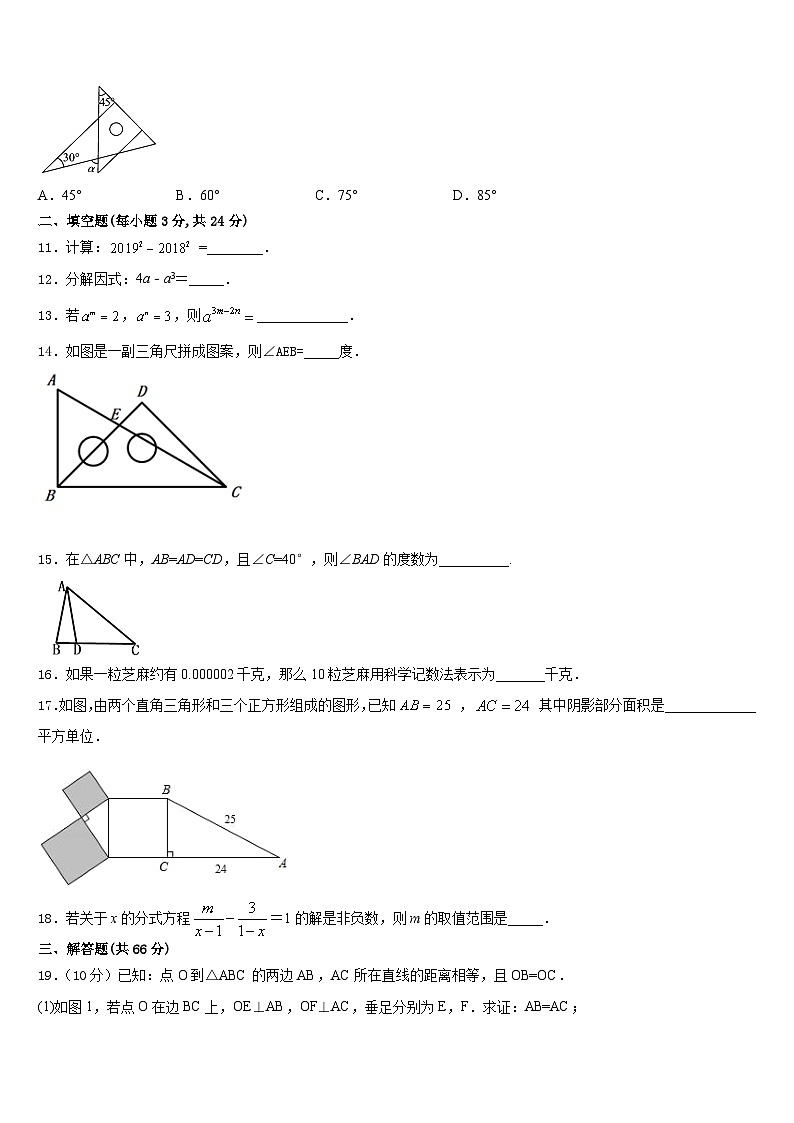
10．将一副直角三角板按如图所示的位置放置，使含30°角的三角板的一条直角边和含45°角的三角板的一条直角边放在同一条直线上，则∠α的度数是（ ）.
A．45°B．60°C．75°D．85°
二、填空题(每小题3分,共24分)
11．计算： =________．
12．分解因式：4a﹣a3＝_____．
13．若，，则_____________．
14．如图是一副三角尺拼成图案，则∠AEB=_____度．
15．在△ABC中，AB=AD=CD，且∠C=40°，则∠BAD的度数为__________.
16．如果一粒芝麻约有0.000002千克，那么10粒芝麻用科学记数法表示为_______千克．
17．如图，由两个直角三角形和三个正方形组成的图形，已知 ， 其中阴影部分面积是_____________平方单位．
18．若关于x的分式方程＝1的解是非负数，则m的取值范围是_____．
三、解答题(共66分)
19．（10分）已知：点O到△ABC的两边AB，AC所在直线的距离相等，且OB=OC．
(1)如图1，若点O在边BC上，OE⊥AB，OF⊥AC，垂足分别为E，F．求证：AB=AC；
(2)如图，若点O在△ABC的内部，求证：AB=AC；
(3)若点O在△ABC的外部，AB=AC成立吗？请画出图表示．
20．（6分）如图所示，在正方形网格中，若点的坐标是，点的坐标是，按要求解答下列问题：
(1)在图中建立正确的平面直角坐标系，写出点C的坐标.
(2)在图中作出△ABC关于x轴对称的△A1B1C1.
21．（6分）在中，，点在边上，且是射线上一动点(不与点重合，且)，在射线上截取，连接．
当点在线段上时，
①若点与点重合时，请说明线段；
②如图2，若点不与点重合，请说明；
当点在线段的延长线上时，用等式表示线段之间的数量关系(直接写出结果，不需要证明)．
22．（8分）基本图形：在RT△ABC中，AB=AC，D为BC边上一点（不与点B，C重合），将线段AD绕点A逆时针旋转90°得到AE．
探索：（1）连接EC，如图①，试探索线段BC，CD，CE之间满足的等量关系，并证明结论；
（2）连接DE，如图②，试探索线段DE，BD，CD之间满足的等量关系，并证明结论；
联想：（3）如图③，在四边形ABCD中，∠ABC=∠ACB=∠ADC=45°，若BD=7，CD=2，则AD的长为 ．

23．（8分）定义:如果一个三角形的一个内角等于另一个内角的两倍，则称这样的三角形为“倍角三角形”．
（1）如图1，△ABC中，AB=AC，∠A为36°，求证：△ABC 是锐角三角形；
（2）若△ABC是倍角三角形，，∠B=30°，AC=，求△ABC面积；
（3）如图2，△ABC的外角平分线AD与CB的延长线相交于点D，延长CA到点E，使得AE=AB，若AB+AC=BD，请你找出图中的倍角三角形，并进行证明．

24．（8分）如图，已知△ABC的三个顶点的坐标分别为A（-5,0）、B（-2,3）、C（-1,0）.
（1）画出△ABC关于原点O成中心对称的图形△A′B′C′；
（2）将△ABC绕原点O顺时针旋转90°，画出对应的△A″B″C″，并写出点B″的坐标.
25．（10分）一辆汽车行驶时的耗油量为0.1升/千米，如图是油箱剩余油量（升）关于加满油后已行驶的路程（千米）的函数图象.
（1）根据图象，直接写出汽车行驶400千米时，油箱内的剩余油量，并计算加满油时油箱的油量；
（2）求关于的函数关系式，并计算该汽车在剩余油量5升时，已行驶的路程.
26．（10分） “绿水青山就是金山银山”，随着生活水平的提高人们对饮水品质的需求越来越高，岳阳市槐荫公司根据市场需求代理，两种型号的净水器，每台型净水器比每台型净水器进价多元，用万元购进型净水器与用万元购进型净水器的数量相等
（1）求每台型、型净水器的进价各是多少元？
（2）槐荫公司计划购进，两种型号的共台进行试销，，购买资金不超过万元．试求最多可以购买型净水器多少台？
参考答案
一、选择题(每小题3分,共30分)
1、C
2、C
3、D
4、D
5、C
6、C
7、C
8、A
9、D
10、C
二、填空题(每小题3分,共24分)
11、1
12、a（2+a）（2﹣a）．
13、
14、75º
15、20°
16、2×10-1．
17、49
18、m≥﹣4且m≠﹣1
三、解答题(共66分)
19、（1）见解析；（2）见解析；（3）不一定成立，见解析．
20、 (1)见解析；C(3，2)；(2)见解析.
21、（1）①证明见解析；②证明见解析；（2）BF＝AE-CD
22、（1）结论：．证明见解析；（2）结论：．证明见解析；（3）
23、（1）证明见解析；（2）；（3）△ADC是倍角三角形，证明见解析．
24、见解析
25、（1）汽车行驶400千米，剩余油量30升，加满油时，油量为70升；（2）已行驶的路程为650千米.
26、（1）A型净水器每台的进价为2000元，B型净水器每台的进价为1800元;
（2）最多可以购买A型净水器40台.