2023-2024学年湖南省澧县张公庙中学八上数学期末预测试题含答案

这是一份2023-2024学年湖南省澧县张公庙中学八上数学期末预测试题含答案，共7页。试卷主要包含了下列命题是假命题的是，在直角坐标系中，点A等内容，欢迎下载使用。

学校_______ 年级_______ 姓名_______
注意事项：
1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。
2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号。回答非选择题时，将答案写在答题卡上，写在本试卷上无效。
3．考试结束后，将本试卷和答题卡一并交回。
一、选择题(每小题3分,共30分)
1．下列命题：
①有一条直角边和斜边对应相等的两个直角三角形全等；
②周长相等的两个三角形是全等三角形
③全等三角形对应边上的高、中线、对应角的角平分线相等；
其中正确的命题有（ ）
A．个B．个C．个D．个
2．如图，木工师傅在做完门框后，为防止变形常常象图中所示那样钉上两条斜拉的木条图中的AB，CD两根木条，这样做是运用了三角形的
A．全等性B．灵活性C．稳定性D．对称性
3．等腰三角形两边长分别为4和8，则这个等腰三角形的周长为（ ）
A．16B．18C．20D．16或20
4．下列命题是假命题的是
A．全等三角形的对应角相等B．若||＝－，则a>0
C．两直线平行，内错角相等D．只有锐角才有余角
5．已知点Q与点P(3，－2)关于x轴对称，那么点Q的坐标为( )
A．(-3，2)B．(3，2)C．(-3，-2)D．(3，-2)
6．在直角坐标系中，点A（–2，2）与点B关于轴对称，则点B的坐标为（ ）
A．（–2，2）B．（–2，–2）C．（2，–2）D．（2，2）
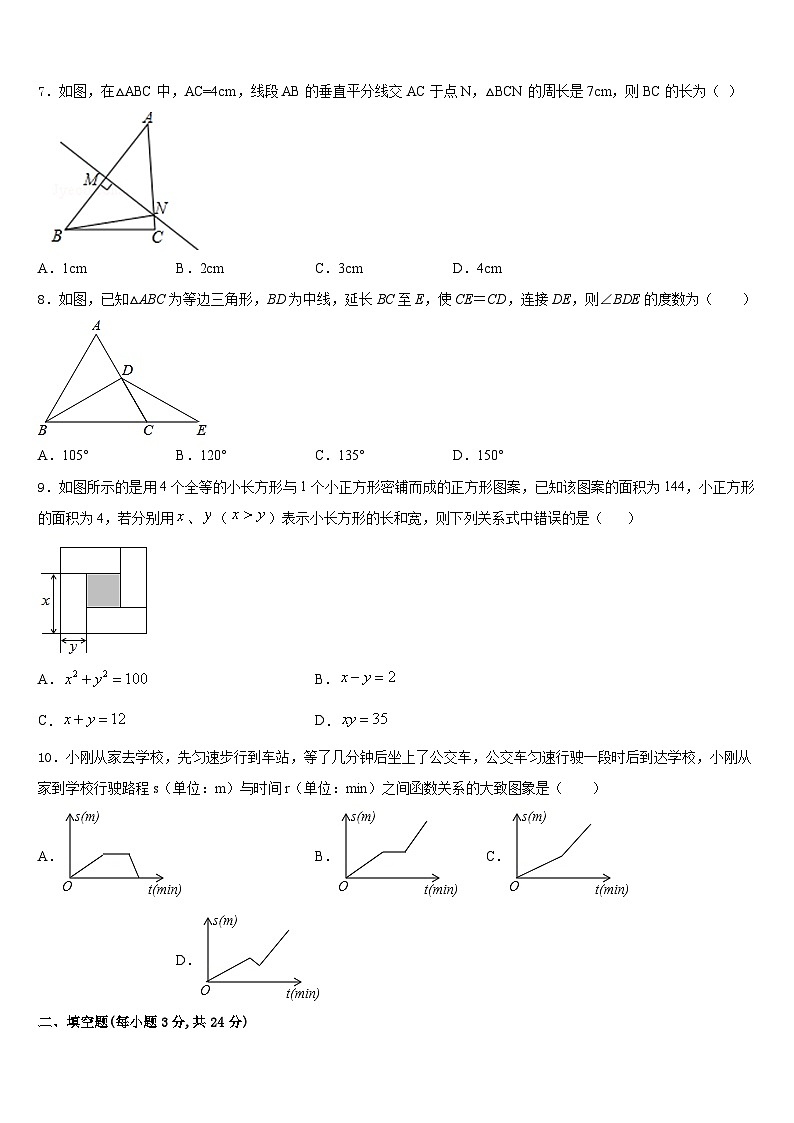
7．如图，在△ABC中，AC=4cm，线段AB的垂直平分线交AC于点N，△BCN的周长是7cm，则BC的长为（ ）
A．1cmB．2cmC．3cmD．4cm
8．如图，已知△ABC为等边三角形，BD为中线，延长BC至E，使CE＝CD，连接DE，则∠BDE的度数为（ ）
A．105°B．120°C．135°D．150°
9．如图所示的是用4个全等的小长方形与1个小正方形密铺而成的正方形图案，已知该图案的面积为144，小正方形的面积为4，若分别用、（）表示小长方形的长和宽，则下列关系式中错误的是（ ）
A．B．
C．D．
10．小刚从家去学校，先匀速步行到车站，等了几分钟后坐上了公交车，公交车匀速行驶一段时后到达学校，小刚从家到学校行驶路程s（单位：m）与时间r（单位：min）之间函数关系的大致图象是（ ）
A．B．C．D．
二、填空题(每小题3分,共24分)
11．若的整数部分为，则满足条件的奇数有_______个．
12．已知关于的分式方程的解为正数，则的取值范围为________．
13．如图，BE平分∠ABC，CE平分外角∠ACD，若∠A＝52°，则∠E的度数为_____．
14．如图，中，，为的角平分线，与相交于点，若，，则的面积是_____．
15．如图，等边的边垂直于轴，点在轴上已知点，则点的坐标为____．
16．化简 结果是_______ ．
17．某鞋店有甲、乙两款鞋各30双，甲鞋每双200元，乙鞋每双50元，该店促销的方式为：买一双甲鞋，送一双乙鞋；只买乙鞋没有任何优惠．打烊后得知．此两款鞋共卖得2750元，还剩鞋共25双，设剩甲鞋x双，乙鞋y双，则依题意可列出方程组
18．计算的结果等于_______．
三、解答题(共66分)
19．（10分）通过学习，甲、乙同学对喀斯特地貌都很感兴趣，为了更直观地了解喀斯特地貌，他们相约在国庆节期间区万峰林．已知甲、乙两同学从家到万峰林的距离均约为3000米，甲同学步行去万峰林，乙同学骑自行车去万峰林，甲步行的速度是乙骑自行车速度的，甲、乙两同学同时从家出发去万峰林，结果乙同学比甲同学早到10分钟．
（1）乙骑自行车的速度；
（2）当乙到达万峰林时，甲同学离万峰林还有多远？
20．（6分）如图，在中，是的平分线，于，于，试猜想与之间有什么关系？并证明你的猜想．
21．（6分）如图，在平面直角坐标系中，直线l1的解析式为y＝x，直线l2的解析式为y＝－x＋3，与x轴、y轴分别交于点A、点B，直线l1与l2交于点C．点P是y轴上一点.
(1)写出下列各点的坐标：点A(，)、点B(，)、点C(，)；
(2)若S△COP＝S△COA,请求出点P的坐标；
(3)当PA＋PC最短时，求出直线PC的解析式.
22．（8分）如图，△ABC三个顶点的坐标分别为A（1，1），B（4，2），C（3，4）．
（1）若△A1B1C1与△ABC关于y轴成轴对称，则△A1B1C1三个顶点坐标分别为A1 ，B1 ，C1 ；
（2）在x轴上找一点P，使PA+PB的值最小，请直接写出点P的坐标是 ．
（3）在y轴上是否存在点Q．使得S△ACQ＝S△ABC，如果存在，求出点Q的坐标，如果不存在，说明理由．
23．（8分）计算：- +．
24．（8分）解下列方程.
(1)
(2)
25．（10分）某次歌唱比赛，三名选手的成绩如下：
（1）若按三项的平均值取第一名，谁是第一名；
（2）若三项测试得分按3：6：1的比例确定个人的测试成绩，谁是第一名？
26．（10分）如图，在等边中，分别为的中点，延长至点，使，连结和．
（1）求证：
（2）猜想：的面积与四边形的面积的关系，并说明理由．
参考答案
一、选择题(每小题3分,共30分)
1、B
2、C
3、C
4、B
5、B
6、B
7、C
8、B
9、A
10、B
二、填空题(每小题3分,共24分)
11、9
12、k＞﹣2且k≠﹣1
13、26°
14、1
15、
16、
17、．
18、2
三、解答题(共66分)
19、（1）乙骑自行车的速度为 m/min；（2）当乙到达万峰林时，甲同学离万峰林还有1500m．
20、详见解析
21、（1）A（6，0），B（0,3），C（2,2）；(2) P（0，）；（3）直线PC的解析式为
22、（1）（﹣1，1），（﹣4，2），（﹣3，4）；（2）（2，0）；（3）存在，或.
23、1
24、（1）是该方程的解；（2）是该方程的解.
25、（1）甲将得第一名；（2）乙将得第一名．
26、（1）见解析；（2）相等，理由见解析．
测试项目
测试成绩
甲
乙
丙
创新
72
85
67
唱功
62
77
76
综合知识
88
45
67