四川省成都市玉林中学2023-2024学年高一上学期12月诊断性考试数学试题（Word版附解析）

这是一份四川省成都市玉林中学2023-2024学年高一上学期12月诊断性考试数学试题（Word版附解析），共16页。试卷主要包含了单选题，多选题，填空题，解答题等内容，欢迎下载使用。

满分：150分 考试时间：120分钟
一、单选题（每题5分，共40分）
1. 已知集合，，则（ ）
A. B. C. D.
【答案】D
【解析】
【分析】根据集合的描述法转化得集合，再根据并集运算即可.
【详解】因为，又
所以.
故选：D.
2. 设，则一定成立的是（ ）
A. B. C. D.
【答案】D
【解析】
【分析】通过取特殊值，即可判断出ABC的正误，利用不等式的性质即可判断出D的正误．
【详解】因为，
选项A中，取，，可知，因此不正确；
选项B中，取，，可知和不存在，因此不正确；
选项C中，取，，可知，因此不正确；
选项D中，由，根据不等式的性质，可知正确.
故选：D.
【点睛】本题考查了不等式的基本性质、特殊值法判断不等式是否成立，属于简单题.
3. 函数的零点所在的区间为
A. B. C. D.
【答案】D
【解析】
【分析】
首先可以根据函数和函数的单调性判断出函数的单调性，然后根据即可得出结果。
【详解】因为函数是减函数，函数是增函数，
所以函数是减函数，
因为，，
所以函数在区间上有零点，
故选D。
【点睛】本题考查二分法判断函数零点所在区间以及复合函数的单调性，复合函数的单调性可结合组成复合函数的基本初等函数的单调性来判断，考查推理能力与运算能力，体现了综合性，是中档题。
4. 下列与的终边相同的角的表达式中，正确的是（ ）
A. B.
C. D.
【答案】B
【解析】
【分析】AC项角度与弧度混用，排除AC；D项终边在第三象限，排除D.
【详解】因为，终边落在第四象限，且与角终边相同，
故与的终边相同的角的集合
即选项B正确；
选项AC书写不规范，选项D表示角终边在第三象限.
故选：B.
5. 已知，，，则a，b，c的大小关系是（ ）
A. B. C. D.
【答案】C
【解析】
【分析】利用指数函数与对数函数的单调性，结合临界值即可得解.
【详解】因为在上单调递减，
所以，，即，，
因为在上单调递减，且恒成立，
所以，即，
所以.
故选：C.
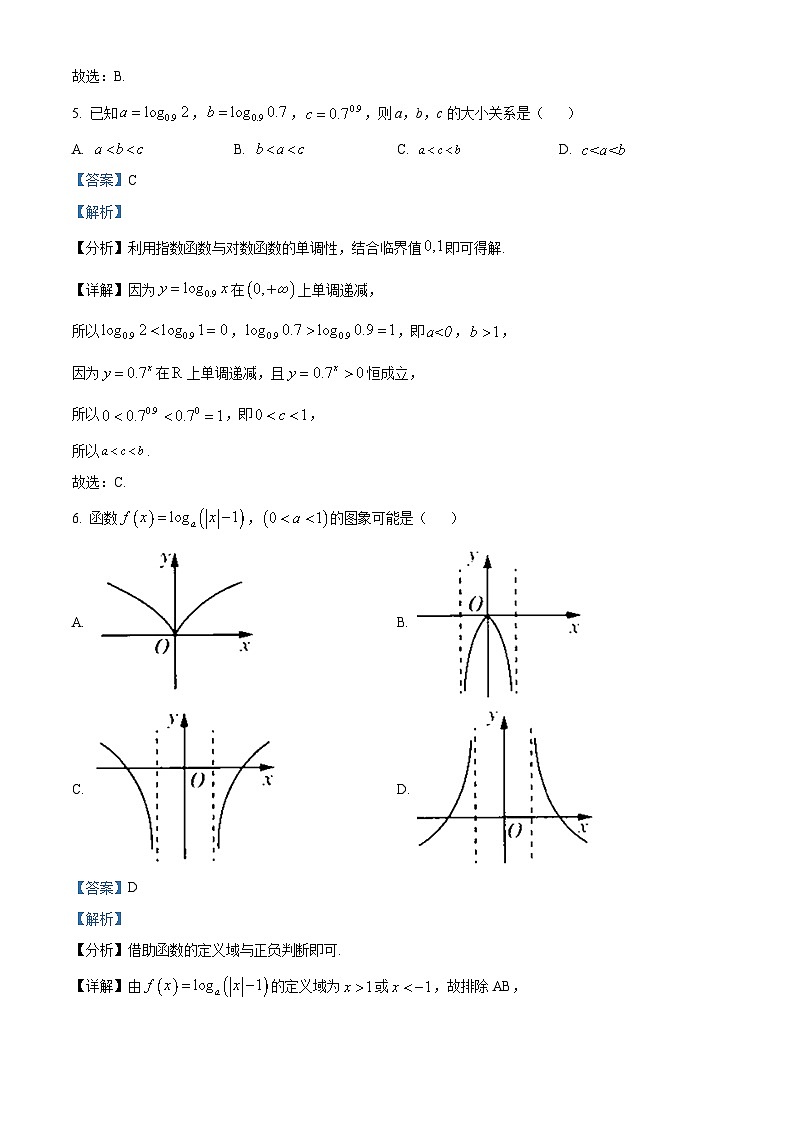
6. 函数，的图象可能是（ ）
A. B.
C. D.
【答案】D
【解析】
【分析】借助函数的定义域与正负判断即可.
【详解】由的定义域为或，故排除AB，
又,则，
,
故排除C.
故选：D.
7. 已知，，且，则（ ）
A. 为定值B. 的最小值为
C. 为定值D. 的最小值为6
【答案】B
【解析】
【分析】根据基本不等式即可根据选项逐一求解.
【详解】由，，且得，当且仅当时取等号，故A不正确，
，当且仅当时取等号，故B正确,
，当且仅当时取等号，故C错误，
，当且仅当时取等号，故D错误.
故选：B
8. 设函数，若关于x的方程（）有四个实数解，且，则的取值范围为（ ）
A. B.
C. D.
【答案】A
【解析】
【分析】作出函数图像，由图像得出函数单调性，再作直线由直线与函数图像交点得满足的性质，再求得其范围．
【详解】如图所示：
因为关于x的方程（）有四个实数解，且，，所以.的对称轴为，所以.
因为，所以，即，.因为，所以.
所以，令，，
因为，为减函数，所以.
故选：A.
【点睛】本题考查方程解的问题，解题方法是把方程的解转化为直线与函数图像交点问题，作出函数图像与直线，利用数形结合思想得出解具有的性质，然后再求解.
二、多选题（部分选对得2分，选错0分，全对5分，共20分）
9. 对于给定的实数a，关于实数x的一元二次不等式的解集可能为（ ）
A. B.
C. D. 或
【答案】BC
【解析】
【分析】讨论两根大小解一元二次不等式.
【详解】当时，函数开口向下
若，不等式解集为
若，不等式的解集为
若，不等式的解集为
综上所述：B、C项都可能成立．
故选：BC.
10. 对于函数，下面几个结论中正确的是（ ）
A. 函数是奇函数B. 函数是偶函数
C. 函数的值域为D. 函数在上是增函数
【答案】ACD
【解析】
【分析】利用函数奇偶性的定义判断AB，利用不等式的性质判断C，利用复合函数的单调性，结合奇函数的对称性判断D，从而得解.
【详解】因为的定义域是R，
又，所以是奇函数，故A正确，B错误；
因为，所以，故C正确；
因为函数在上可化为，
所以奇函数在上是增函数，且在处连续，
则在其定义域内是增函数，故D正确，
故选：ACD．
11. 给出下列四个语句，其中不正确的是（ ）
A. 若且，则
B. 在同一坐标系中，与的图象关于直线y=x对称
C. 函数的定义域为，则函数的定义域为
D. 的增区间是，减区间是
【答案】ACD
【解析】
【分析】根据时，没有意义，可判定A不正确；根据指数函数和对数函数互为反函数，可判定B正确；根据抽象函数的定义域的求解，可判定C不正确；根据复合函数的单调性的判定方法，可判定D不正确.
【详解】对于A中，当时，没有意义，所以命题“若且，则”所以A不正确；
对于B中，根据指数函数和对数函数互为反函数，所以在同一坐标系中，与的图象关于直线对称，所以B正确；
对于C，由函数的定义域为，即，
则，解得，所以函数的定义域为，所以C不正确；
对于D中，由不等式，解得，
又由函数，可得在上单调递增，在单调递减.
所以函数在上单调递增，在单调递减，所以D不正确.
故选：ACD.
12. 高斯是德国著名的数学家，用其名字命名的“高斯函数”为：设，用表示不超过的最大整数，则称为高斯函数，例如：，.已知函数，，则关于函数的叙述中正确的是（ ）
A.
B. 函数的值域为
C. 在R上为增函数
D. 函数在区间有12个零点
【答案】AB
【解析】
【分析】画出的图象，结合图象逐项判断可得答案.
【详解】
画出的图象，
根据“高斯函数”的定义，故 A正确；
由图象可得函数的值域为，故B正确；
由图象可得在R上不是增函数，故C错误；
由函数在区间有13个零点，故D错误.
故选：AB.
三、填空题（每题5分，共20分）
13. 角所在象限是____________.
【答案】第四象限
【解析】
【分析】把角写成，， 的形式，根据的终边位置，做出判断．
【详解】解：，故与终边相同，故角在第四象限．
故答案为：第四象限．
【点睛】本题主要考查终边相同的角的定义和表示方法，象限角、象限界角的定义，属于基础题．
14. 若一元二次方程有两个正根，求的取值范围__________．
【答案】
【解析】
分析】
设两根为，由一元二次方程有两个正根，根据根的判别式和韦达定理，列式即可得解.
【详解】设两根为，根据题意可得：
由且，
又有：，，
解得：
故答案为：
15. 已知，方程的实根个数为__________．
【答案】2
【解析】
【分析】分别作出和的图象，结合图象即可得到答案．
【详解】由，则，
则令，，
分别作出它们的图象如下图所示，

由图可知，有两个交点，所以方程的实根个数为2．
故答案：2．
16. 若，，，，则最小值为______．
【答案】##
【解析】
【分析】令 ，则，由此可将变形为，结合基本不等式，即可求得答案。
【详解】由题意，，，，得：，
设 ，则 ，
故
，
当且仅当 ，即 时取得等号，
故的最小值为，
故答案为：
四、解答题（共6题，满分70分）
17. 求值：
（1）；
（2）
【答案】（1）2 （2）
【解析】
【分析】（1）利用分数指数幂运算和根式运算法则计算出答案；
（2）利用指数和对数运算法则计算.
【小问1详解】
原式=
【小问2详解】
原式=
18. 已知，求下列各式的值：
（1）；
（2）.
【答案】（1）；
（2）.
【解析】
【分析】（1）求出的值，利用诱导公式结合弦化切可求得结果；
（2）代数式上除以，再结合弦化切可求得结果.
【小问1详解】
解：因为，则，
原式.
【小问2详解】
解：原式.
19. 已知函数，且，.
（1）求，的值，并判断的奇偶性；
（2）试判断函数在上的单调性，并证明.
【答案】（1），，偶函数
（2）在上为减函数，证明见解析；
【解析】
【分析】（1）由已知条件列方程组解得即可求出，的值，从而得到的解析式，根据函数奇偶性定义判断即可；
（2）利用函数单调性定义判断即可；
【小问1详解】
由已知可得，即，
所以，解得．
所以，定义域为，
且，
所以为偶函数．
【小问2详解】
在上为减函数，证明如下：
任取，且，
则
．
因为，且，所以，
从而，，，
故，即，
所以函数在上为减函数．
20. 某科研团队在某水域放入一定量水葫芦进行研究，发现其蔓延速度越来越快，经过2个月其覆盖面积约为18 m2，经过3个月其覆盖面积约为27 m2. 现水葫芦覆盖面积y（单位:m2）与经过个月的关系有两个函数模型与可供选择.（参考数据:lg 2≈0.301 0，lg 3≈0.477 1）
（1）试判断哪个函数模型更合适，并求出该函数模型的解析式;
（2）约经过几个月该水域中水葫芦面积至少是当初投放的100倍?
【答案】（1）；
（2）约经过12个月该水域中水葫芦面积至少是当初投放的100倍.
【解析】
【分析】（1）根据函数的增长速度的不同来选择函数模型,用待定系数法求出函数解析式；
（2）根据题目列出指数不等式求解即可.
【小问1详解】
∵的增长速度越来越快，的增长速度越来越慢，
∴依题意应选函数，
则 解得，
故；
【小问2详解】
由（1）知，当时，，
设经过x个月该水域中水葫芦面积至少是当初投放的100倍，则，
则，
故，
∵x∈N+，故.
即约经过12个月该水域中水葫芦面积至少是当初投放的100倍.
21. 已知集合，.
（1）求集合；
（2）已知命题：，命题：，若是的充分不必要条件，求实数的取值范围.
【答案】（1）
（2）
【解析】
【分析】（1）将含对数的不等式转化为整式不等式求解即可；
（2）求出，分，，讨论，通过集合的包含关系列式计算即可.
【小问1详解】
集合中不等式即，
也即
令，得，解得，
即，得，
故.
【小问2详解】
因为是的充分不必要条件，所以，
又由得，即，即，
当，即时，，
此时必有；
当，即时，
此时必有；
当，即时，，
，
，即，，
综上所述：.
22. 已知函数在区间[2，3]上有最大值4和最小值1，设.
（1）求，的值
（2）若不等式在上有解，求实数的取值范围；
（3）若有三个不同的实数解，求实数的取值范围.
【答案】（1）；（2）；（3）．
【解析】
【分析】（1）判断函数在上的单调性，得出最大值和最小值，由此可求得；
（2）设，利用分离参数法，题中问题为在上有解，求出的最大值即可得．
（3）把方程化简，并设，方程化为，结合图象，方程有两个实数解，则有，，或，，利用二次方程根的分布知识求得的范围．
【详解】（1）由题意，又，∴在上单调递增，
∴，解得．
（2）由（1），，
时，，令，则在上有解，
，∵，∴，
，则，∴的最大值为，
∴，即．
∴的取值范围是．
（3）原方程化为，
令，则，有两个实数解，
作出函数的图象，如图
原方程有三个不同的实数解，则，，或，，
记，
则，解得，
或，无解．
综上的取值范围是．
【点睛】本题考查函数的单调性，考查不等式有解，考查根据函数零点求参数范围问题，解题关键是掌握利用零点存在定理构建不等式求解，分离参数后转化为函数函数的最值，涉及到几个零点时，还要老考虑函数图象与直线的交点个数，本题考查了分析问题与解决问题的能力，考查运算求解能力．