陕西省渭南市富平县淡村镇南社初级中学2023-2024学年九年级上学期期末模拟数学试题

这是一份陕西省渭南市富平县淡村镇南社初级中学2023-2024学年九年级上学期期末模拟数学试题，共11页。试卷主要包含了答卷前将装订线内的项目填写清楚，围棋起源于中国，棋子分黑白两色等内容，欢迎下载使用。
九年级数学
注意事项：
1．本试卷共6页，满分120分，时间120分钟，学生直接在试题上答卷；
2．答卷前将装订线内的项目填写清楚．
一、选择题（共8小题，每小题3分，计24分．每小题只有一个选项是符合题意的）
1．已知关于的一元二次方程的一个解是，则的值为（ ）
A．B．1C．D．2
2．如图，是某几何体的俯视图，该几何体是（ ）
（第2题图）
A．B．C．D．
3．如图，，两条直线与这三条平行线分别交于点和，已知，若，则的长为（ ）
（第3题图）
A．2B．3C．5D．6
4．若关于的方程有实数根，则实数的取值范围是（ ）
A．B．C．D．
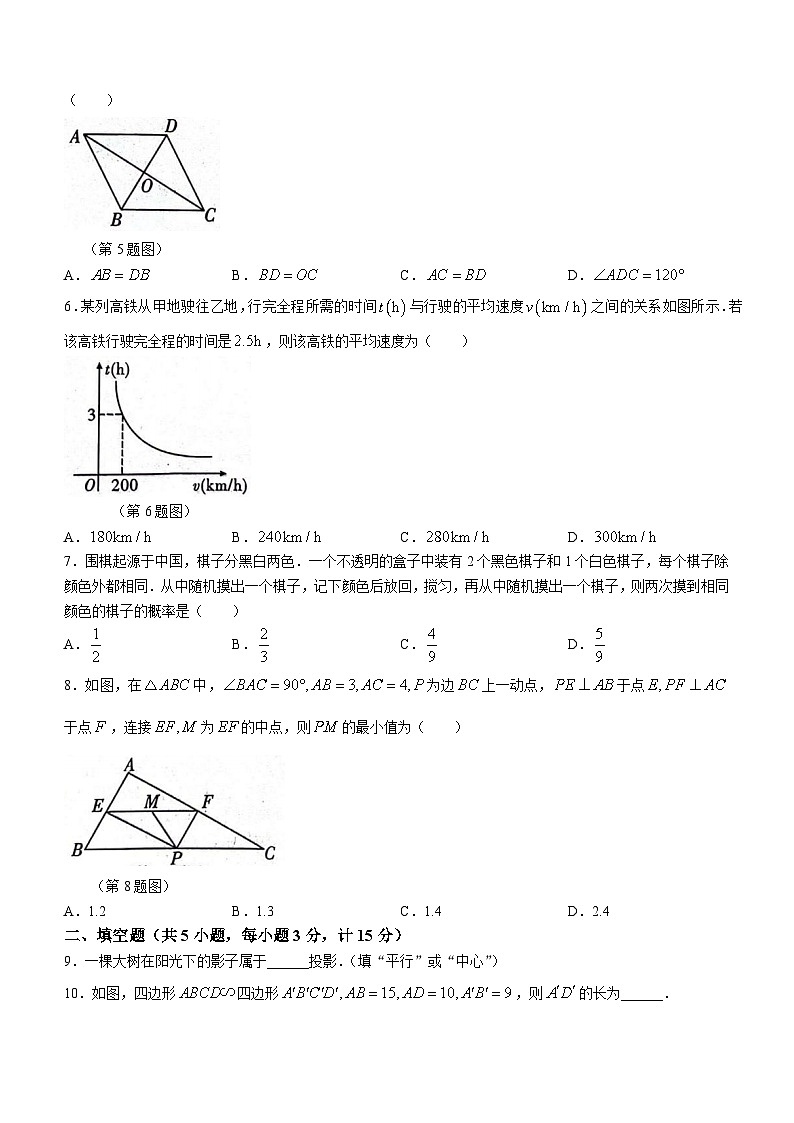
5．如图，在菱形中，对角线相交于点，添加下列条件，能使菱形成为正方形的是（ ）
（第5题图）
A．B．C．D．
6．某列高铁从甲地驶往乙地，行完全程所需的时间与行驶的平均速度之间的关系如图所示．若该高铁行驶完全程的时间是，则该高铁的平均速度为（ ）
（第6题图）
A．B．C．D．
7．围棋起源于中国，棋子分黑白两色．一个不透明的盒子中装有2个黑色棋子和1个白色棋子，每个棋子除颜色外都相同．从中随机摸出一个棋子，记下颜色后放回，搅匀，再从中随机摸出一个棋子，则两次摸到相同颜色的棋子的概率是（ ）
A．B．C．D．
8．如图，在中，为边上一动点，于点于点，连接为的中点，则的最小值为（ ）
（第8题图）
A．1.2B．1.3C．1.4D．2.4
二、填空题（共5小题，每小题3分，计15分）
9．一棵大树在阳光下的影子属于______投影．（填“平行”或“中心”）
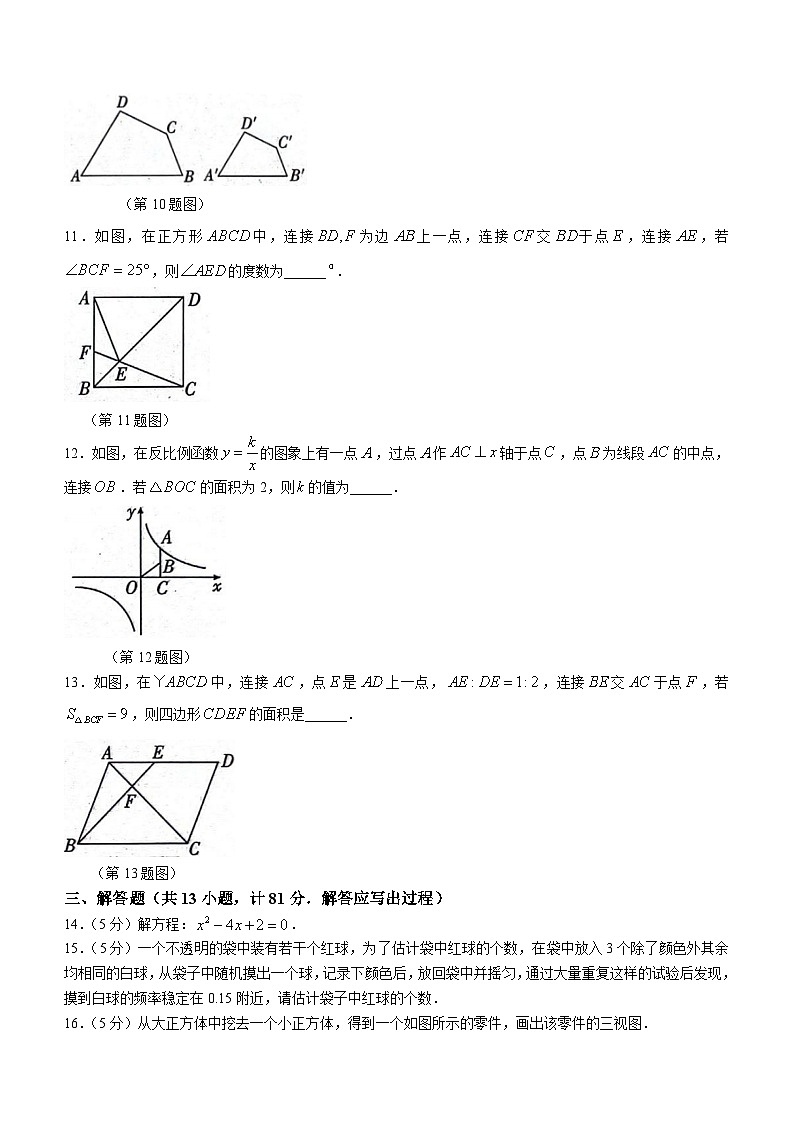
10．如图，四边形四边形，则的长为______．
（第10题图）
11．如图，在正方形中，连接为边上一点，连接交于点，连接，若，则的度数为______．
（第11题图）
12．如图，在反比例函数的图象上有一点，过点作轴于点，点为线段的中点，连接．若的面积为2，则的值为______．
（第12题图）
13．如图，在中，连接，点是上一点，，连接交于点，若，则四边形的面积是______．
（第13题图）
三、解答题（共13小题，计81分．解答应写出过程）
14．（5分）解方程：．
15．（5分）一个不透明的袋中装有若干个红球，为了估计袋中红球的个数，在袋中放入3个除了颜色外其余均相同的白球，从袋子中随机摸出一个球，记录下颜色后，放回袋中并摇匀，通过大量重复这样的试验后发现，摸到白球的频率稳定在0.15附近，请估计袋子中红球的个数．
16．（5分）从大正方体中挖去一个小正方体，得到一个如图所示的零件，画出该零件的三视图．
（第16题图）
17．（5分）关于的一元二次方程，方程的两根分别为，且，求的值．
18．（5分）如图，在四边形中，，点是四边形内一点，连接，求证：四边形是菱形．
（第18题图）
19．（5分）唐诗是中华民族珍贵的文化遗产之一，是中华文化宝库中的一颗明珠．在一个不透明的盒子里放有四张大小、形状及质地相同的卡片，卡片上分别写有李白的《静夜思》，高适的《别董大》，孟浩然的《春晓》和王维的《相思》四首诗．
（第19题图）
（1）若小明从盒子中随机抽取1张卡片，则卡片上诗的作者是李白的概率是______；
（2）小明先从盒子中随机抽取1张卡片（不放回），小亮再从余下的3张卡片中随机抽取1张，用列表法或画树状图法求两人中恰好有一人抽中的卡片上诗的作者是孟浩然的概率．
20．（5分）如图，三个顶点坐标分别为，以原点为位似中心，将放大为原来的2倍得到，点的对应点分别为．
（第20题图）
（1）在图中第一象限内画出符合要求的；
（2）在（1）的条件下，写出点的坐标．
21．（6分）已知反比例函数的图象位于第二、四象限．
（1）求的取值范围；
（2）若点是该反比例函数图象上的两点，试比较函数值的大小．
22．（7分）如图，已知四边形是平行四边形，对角线交于点是等边三角形．
（第22题图）
（1）求证：四边形是矩形；
（2）若，求的长．
23．（7分）如图，用长为的篱笆，一面利用墙（墙的最大可用长度为，靠墙一面不用篱笆），围成中间隔有一道篱笆的长方形花圃（中间的篱笆把长方形花圃分成两个小长方形），为了方便出入，在建造篱笆花圃时，在上用其他材料做了宽为的两扇小门．
（第23题图）
（1）设花圃的宽长为，请你用含的代数式表示的长为______m；
（2）若围成的花圃总面积是，求此时花圃的宽．
24．（8分）如图，在一次测量操场旗杆高度的数学活动课上，小刚拿一根高的竹竿直立在离旗杆的点处（即），然后走到点处，这时目测到旗杆顶部与竹竿顶部恰好在同一直线上，又测得两点间的距离为，小刚的目高（眼睛到地面的距离）为，且，点在同一水平直线上，求旗杆的高度．
（第24题图）
25．（8分）如图，正比例函数与反比例函数的图象交于点，点在反比例函数图象上，过点作轴于点．
（第25题图）
（1）求反比例函数的表达式；
（2）点在第一象限且在反比例函数的图象上，，求点的坐标．
26．（10分）【问题发现】
（1）如图①，正方形的两边分别在正方形的边和上，连接，则的度数为______；
【问题探究】
（2）将图①中的正方形绕点逆时针旋转，如图②，在旋转的过程中，的值是否为定值，若是定值，请求出这个值，若不是，请说明理由；
【问题拓展】
（3）如图③，是正方形的对角线，是等腰直角三角形，为的中点．若点在线段上运动，连接，则在点的运动过程中，求线段长的最小值．
（第26题图）
试卷类型：A（北师大版）
2023～2024学年度第一学期期末调研试题（卷）
九年级数学参考答案及评分标准
一、选择题（共8小题，每小题3分，计24分．每小题只有一个选项是符合题意的）
1．A2．B3．D4．C
5．C6．B7．D8．A
二、填空题（共5小题，每小题3分，计15分）
9．平行10．611．7012．8
13．11
三、解答题（共13小题，计81分．解答应写出过程）
14．解：，，，即，
，．
15．解：设估计袋子中红球的个数为个，
根据题意得：，解得，
经检验是原方程的解，估计袋子中红球的个数为17个．
16．解：如图所示．（画对主视图得1分，画对左视图和俯视图各得2分，共5分）
17．解：由根与系数关系得，
，，解得．
18．证明：在和中，，
，，
，四边形是菱形．
19．解：（1）．
（2）列表如下：
由表可知一共有12种情况，两人中恰好有一人抽中的卡片上诗的作者是孟浩然的有6种情况，
两人中恰好有一人抽中的卡片上诗的作者是孟浩然的概率为．
20．解：（1）如图所示．
（2）点的坐标分别为．
21．解：（1）反比例函数的图象位于第二、四象限，
，解得，的取值范围是．
（2）反比例函数的图象位于第二、四象限，
当时，随的增大而增大．
，．
22．（1）证明：四边形是平行四边形，．
是等边三角形，，
，四边形是矩形．
（2）解：四边形是矩形，．
是等边三角形，，则，
．
23．解：（1）．
（2）根据题意，得，
化简得：，解得：．
当时，，符合要求；
当时，，不符合要求，舍去．
答：此时花圃的宽为．
24．解：设，过作于点，交于点（如图），
则四边形和四边形均为矩形，
，
．
，
，，即，
，旗杆的高度为．
25．解：（1）正比例函数与反比例函数的图象交于点，
，解得，点的坐标为，
，反比例函数的表达式为．
（2）轴于点，点的横坐标为2．
点在反比例函数图象上，，即点的坐标为．
点在第一象限，，
，
解得或，点的坐标为或．
26．解：（1）45．
（2）的值是定值，连接，
四边形和四边形都是正方形，
，，
，．
（3）连接．
在正方形中，，
，
，即．
，，
，，当时，最小．
为的中点．．
，，则，
在Rt中，，，
，即线段长的最小值为．
李白
高适
孟浩然
王维
李白
——
（李白，高适）
（李白，孟浩然）
（李白，王维）
高适
（高适，李白）
——
（高适，孟浩然）
（高适，王维）
孟浩然
（孟浩然，李白）
（孟浩然，高适）
——
（孟浩然，王维）
王维
（王维，李白）
（王维，高适）
（王维，孟浩然）
——