专题08 垂径定理、圆心角、圆周角之六大题型-【备考期末】2023-2024学年九年级数学上学期期末真题分类汇编（人教版）

这是一份专题08 垂径定理、圆心角、圆周角之六大题型-【备考期末】2023-2024学年九年级数学上学期期末真题分类汇编（人教版），文件包含专题08垂径定理圆心角圆周角之六大题型原卷版docx、专题08垂径定理圆心角圆周角之六大题型解析版docx等2份试卷配套教学资源，其中试卷共46页， 欢迎下载使用。

利用垂径定理求值
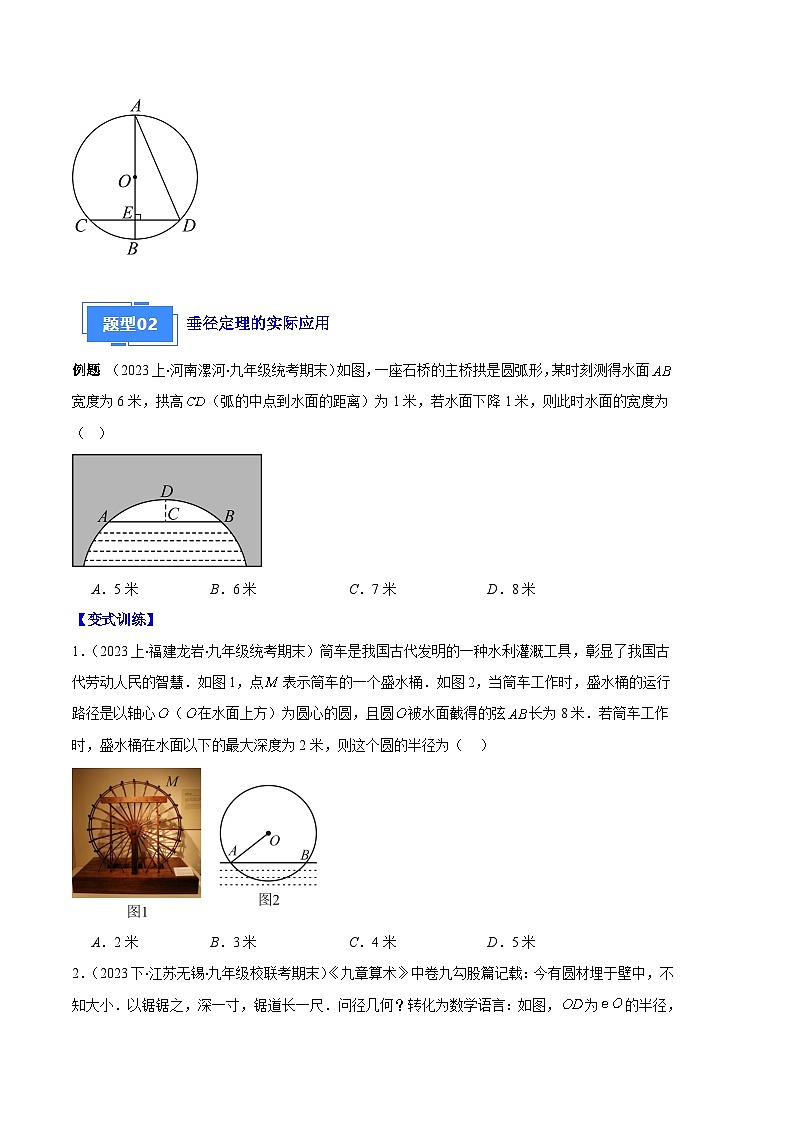
例题：（2023下·江苏泰州·八年级统考期末）如图，是的直径，弦于点，，，则 ．

【变式训练】
1．（2023上·河北张家口·九年级张家口东方中学校考期末）如图，的半径为6cm，是弦，于点C，将劣弧沿弦折叠，交于点D，若D是的中点，则的长为 ．

2．（2023上·辽宁葫芦岛·九年级统考期末）如图，是的直径，弦，垂足为，连接，若，，则弦的长为 ．

垂径定理的实际应用
例题：（2023上·河南漯河·九年级统考期末）如图，一座石桥的主桥拱是圆弧形，某时刻测得水面宽度为6米，拱高（弧的中点到水面的距离）为1米，若水面下降1米，则此时水面的宽度为（ ）
A．5米B．6米C．7米D．8米
【变式训练】
1．（2023上·福建龙岩·九年级统考期末）筒车是我国古代发明的一种水利灌溉工具，彰显了我国古代劳动人民的智慧．如图1，点表示筒车的一个盛水桶．如图2，当筒车工作时，盛水桶的运行路径是以轴心（在水面上方）为圆心的圆，且圆被水面截得的弦长为8米．若筒车工作时，盛水桶在水面以下的最大深度为2米，则这个圆的半径为（ ）
A．2米B．3米C．4米D．5米
2．（2023下·江苏无锡·九年级校联考期末）《九章算术》中卷九勾股篇记载：今有圆材埋于壁中，不知大小．以锯锯之，深一寸，锯道长一尺．问径几何？转化为数学语言：如图，为的半径，弦，垂足为，寸，尺尺寸，则此圆材的直径长是 寸．
利用弧、弦、圆心角的关系求解
例题：（2023上·河北石家庄·九年级统考期末）如图所示，是⊙O的内接三角形，点B是的中点，则下列结论正确的是（ ）
A．B．
C．D．
【变式训练】
1．（2023上·广西河池·九年级统考期末）如图，是的直径，C是的中点，若等于，则的度数为 ．
2．（2023上·江苏镇江·九年级统考期末）如图，点A，B，C都在上，B是的中点，，则等于 ．
半圆（直径）所对的圆周角是直角
例题：（2023上·山东泰安·九年级东平县实验中学校考期末）如图，的直径是，，圆的半径是4，则弦的长是（ ）．

A．B．C．D．
【变式训练】
1．（2023上·广西玉林·九年级统考期末）如图，在中，为的直径，已知，，，，则 ．

2．（2023上·辽宁葫芦岛·九年级统考期末）如图，为的直径，内接于，，交于点E．
(1)求的度数；
(2)若点E为中点，，求的长．
90°的圆周角所对的弦是直径
例题：（2023上·广东汕头·九年级统考期末）如图，四边形内接于，，，．则的长为 ．
【变式训练】
1．（2023上·山东济南·九年级统考期末）如图，正方形中，，点沿线段由向运动（到停止运动），点沿线段由向运动（到停止运动），两点同时出发，速度相同，连接，作于点，则在整个运动过程中点的运动轨迹长为 ．
2．（2022·安徽安庆·校考一模）如图，在中，，，，是内部的一个动点，连接，且满足，过点作于点，则 ；当线段最短时，的面积为

已知圆内接四边形求角度
例题：（2023上·辽宁铁岭·九年级统考期末）如图，四边形内接于，为延长线上的一点，若，则的度数为 ．

【变式训练】
1．（2023上·江苏南京·九年级统考期末）如图，内接于，外角的平分线交于点，射线交延长线于点．若，，则的度数为 °．
2．（2023上·浙江绍兴·九年级统考期末）如图，四边形内接于，分别延长，，使它们相交于点，，且．
(1)求证：．
(2)若，点为的中点，求的半径．
一、单选题
1．（2023上·河北张家口·九年级统考期末）中的一段劣弧的度数为，则（ ）
A．B．C．D．
2．（2023上·河南许昌·九年级统考期末）如图，在中，弦相交于点P，若，，则的大小是（ ）

A．B．C．D．
3．（2023上·河南省直辖县级单位·九年级校联考期末）如图，的半径为，弦的长为，P是弦上一动点，则线段长的最小值为（ ）

A．10B．C．5D．
4．（2023上·江西赣州·九年级统考期末）如图，四边形内接于，若它的一个外角，则的度数为（ ）
A．B．C．D．
5．（2023上·河北邢台·九年级校考期末）筒车是我国古代发明的一种水利灌溉工具，明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理，如图1，筒车盛水桶的运行轨道是以轴心O为圆心的圆，如图2，已知圆心O在水面上方，且被水面截得的弦长为4米，半径长为3米．若点C为运行轨道的最低点，则点C到弦所在直线的距离是（ ）
A．1米B．米C．3米D．米
二、填空题
6．（2023下·山东济宁·九年级统考期末）如图，将沿弦折叠交直径于圆心O，则 度．

7．（2022上·天津滨海新·九年级校考期中）如图，AB，CD是的直径，，若，则的度数是 ．
8．（2023下·江西南昌·九年级统考期末）如图，是半圆O的弦，过圆心O，过O作于点D．若，则 cm．

9．（2023上·浙江宁波·九年级统考期末）在圆中，四点在圆上，，，，则的值为 ．
10．（2023上·山西阳泉·九年级统考期末）如图，在中，，以为直径的半圆交于点，点为的中点，连接．若，，则的长为 ．

三、解答题
11．（2023上·安徽合肥·九年级统考期末）如图，的直径垂直于弦，垂足为E，．
(1)求的半径长；
(2)连接 ，作于点F，求的长．
12．（2023上·湖北荆门·九年级校考期末）某居民小区一处圆柱形的输水管道破裂，维修人员为更换管道，需确定管道圆形截面的半径，下图是水平放置的破裂管道有水部分的截面．
(1)若这个输水管道有水部分的水面宽，水面最深地方的高度为4，求这个圆形截面的半径；
(2)在（1）的条件下，小明把一只宽12的方形小木船放在修好后的圆柱形水管里，已知船高出水面13，问此小船能顺利通过这个管道吗？
13．（2023上·广东广州·九年级校考期末）如图，A是上一点，是直径，点D在上且平分．

(1)连接，求证：平分；
(2)若，求的长．
14．（2023上·江苏宿迁·九年级统考期末）如图，四边形是的内接四边形，且，垂足为，是的直径．

(1)和相等吗？为什么？
(2)过圆心作，垂足为，若，求的长．
15．（2023上·山东威海·九年级统考期末）【初识模型】如图1，在中，．点为边上一点，以为边作，使，，连接，则与的数量关系是__________；
【构建模型】如图2，内接于为的直径，，点为弧上一点，连接．若，求的长；
【运用模型】如图3，等边内接于，点为弧上一点，连接．若，求的长．