

【期中复习】人教版 初中数学九年级上册 期末专题复习 旋转类压轴题专题训练(含解析)
展开(1)求证:;
(2)将图①中的绕点逆时针旋转,连接,点为线段中点,连接,,,如图②.
①求证:,;
②若,求的面积.
2.探究:如图1和2,四边形中,已知,,点,分别在、上,.
(1)①如图 1,若∠B、都是直角,把绕点A逆时针旋转至△ADG,使与重合,则能证得,请写出推理过程;
②如图 2,若∠B、都不是直角,则当∠B与满足数量关系___时,仍有;
(2)拓展:如图3,在中中,,,点、均在边上,且.若,求的长.
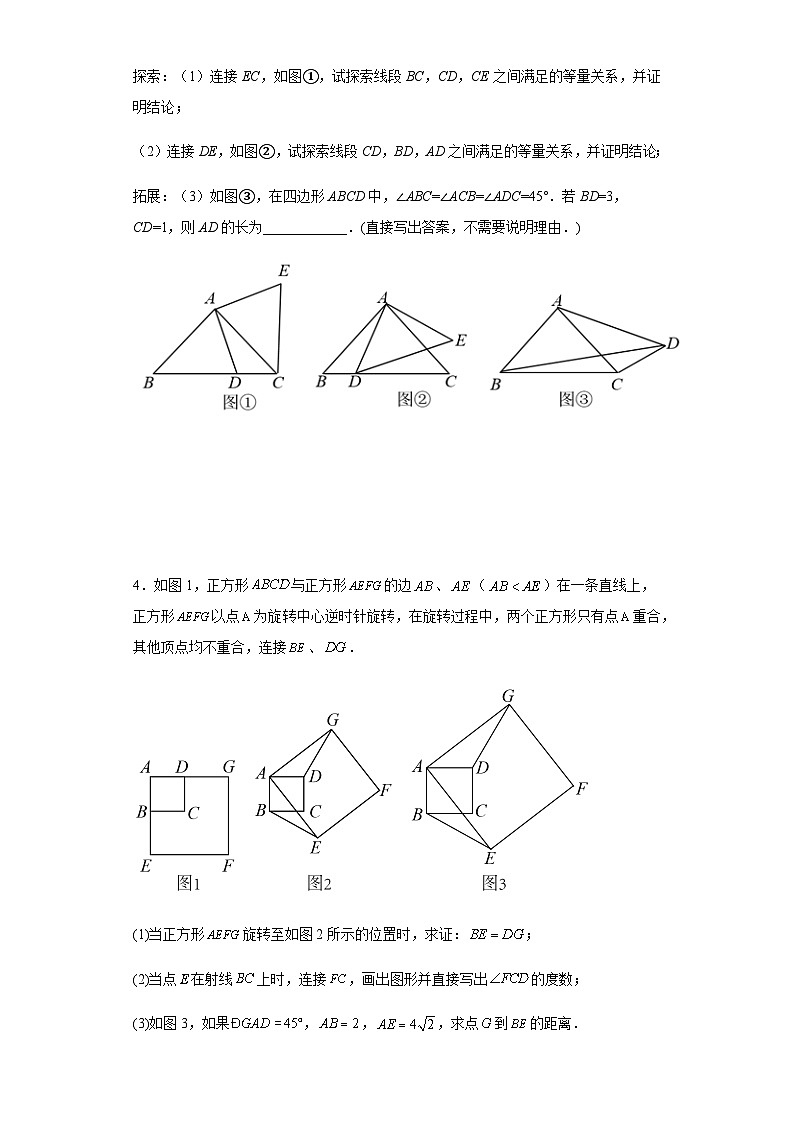
3.基本图形:在Rt△ABC中,AB=AC,D为BC边上一点(不与点B,C重合),将线段AD绕点A逆时针旋转90°得到AE.
探索:(1)连接EC,如图①,试探索线段BC,CD,CE之间满足的等量关系,并证明结论;
(2)连接DE,如图②,试探索线段CD,BD,AD之间满足的等量关系,并证明结论;
拓展:(3)如图③,在四边形ABCD中,∠ABC=∠ACB=∠ADC=45°.若BD=3,CD=1,则AD的长为____________.(直接写出答案,不需要说明理由.)
4.如图1,正方形与正方形的边、()在一条直线上,正方形以点为旋转中心逆时针旋转,在旋转过程中,两个正方形只有点重合,其他顶点均不重合,连接、.
(1)当正方形旋转至如图2所示的位置时,求证:;
(2)当点在射线上时,连接,画出图形并直接写出的度数;
(3)如图3,如果,,,求点到的距离.
5.将一张透明的平行四边形胶片沿对角线剪开,得到图①中的两张三角形胶片和.将这两张三角形胶片的顶点B与顶点E重合,把绕点B顺时针方向旋转,这时AC与DF相交于点O.
(1)当旋转至如图②位置,点B(E),C,D在同一直线上时,∠AFD与∠DCA的数量关系是 .
(2)当继续旋转至如图③位置时,(1)中的结论还成立吗?请说明理由.
(3)在图③中,连接BO,AD,探索BO与AD之间有怎样的位置关系,并证明.
6.如图,△ABC中,∠ACB=90º,AC=BC=1,将△ABC绕点C逆时针旋转角α.(0º<α<90º)得到△A1B1C1,连结BB1.设CB1交AB于D,A1B1分别交AB、AC于E、F.
(1)在图中不再添加其它任何线段的情况下,请你找出一对全等的三角形,并加以证明(△ABC与△A1B1C1全等除外);
(2)当△BB1D是等腰三角形时,求α;
(3)当α=60º时,求BD的长.
7.如图,在等边三角形中,点为内一点,连接,,,将线段绕点A顺时针旋转得到,连接,.
(1)用等式表示与的数量关系,并证明;
(2)当时,
直接写出的度数为______;
若为的中点,连接,用等式表示与的数量关系,并证明.
8.已知,在内部作等腰,,.点D为射线上任意一点,连接,将线段绕点A逆时针旋转得到线段,连接并延长交射线于点F.
(1)如图1,当时,试探究线段与的数量关系并证明;
(2)如图2,当时,(1)中的结论是否还成立?若成立,请给予证明;若不成立,请说明理由;
(3)若,,当点D在直线上运动的过程中,请直接写出的最小值是______.
9.平面直角坐标系中,O为原点,点,点,把绕点B逆时针旋转,得,点A,O旋转后的对应点为,,记旋转角为α.
(1)如图1,若,则点的坐标为 ,点的坐标为 ,的长为 .
(2)如图2,若,求点的坐标;
(3)在(2)的条件下,在坐标平面内有一点D,使A、B、、D四个点构成的四边形是平行四边形,请你直接写出点D的坐标.
10.如图1,在等边三角形中,点在上,连接,将绕点逆时针旋转,得到,过点作交射线于点,交射线于点,使.
(1)如图2,当点与点重合时,求证:为中点;
(2)当点在边上时,求与之间的数量关系;
(3)当点在延长线上时,(2)中的结论是否仍成立,若成立,请证明:若不成立,请说明理由.
11.如图,点P是内一点,
(1)如图1,求证:;
(2)如图2,若 且 求的面积;
(3)如图3,将绕点P旋转至处,过D作,交延长线于F,若 ,直接写出的值为 .
12.已知△ABC是边长为4的等边三角形,点D是射线BC上的动点,将AD绕点A逆时针方向旋转60°得到AE,连接DE.
(1)如图1,猜想△ADE是什么三角形? ;(直接写出结果)
(2)如图2,点D在射线CB上(点C的右边)移动时,∠BCE和∠BAC之间有怎样的数量关系,请说明理由.
(3)当点在线段CB上移动时,△DEC的周长是否存在最小值?若存在.请求出周长的最小值以及此时△DEC的面积;若不存在,请说明理由.
13.在△OAB中,OA=OB,∠AOB=n°,C为平面内一点,连接OC,将OC绕点O逆时针旋转n°得到线段OD,连接AC、BD交于点M.
(1)如图1,若n=35,填空:
①AC与BD的数量关系为 ;
②∠AMB的度数为 ;
(2)如图2,若n=90:
①判断AC与BD之间存在怎样的数量关系?并说明理由;
②求∠AMB的度数;
(3)在(2)的条件下,当∠CAB=30°,且点C与点M重合时,请直接写出OD与OA之间存在的数量关系.
14.在正方形ABCD中,点E,F分别在边BC,CD上,且∠EAF=45°.EA交BD于M,AF交BD于N.
(1)作△APB≌△AND(如图①),求证:△APM≌△ANM;
(2)求证:;
(3)矩形ABCD中,M、N分别在BC、CD上,∠MAN=∠CMN=45°,(如图②),请你直接写出线段MN,BM,DN之间的数量关系.
15.如图,平行四边形ABCD中,.对角线相交于点O,将直线AC绕点O顺时针旋转,分别交于点E,F.
(1)证明:当旋转角为90°时,四边形ABEF是平行四边形;
(2)证明:在旋转过程中,线段AF与EC总保持相等;
(3)在旋转过程中,当AC绕点O顺时针旋转多少度时,四边形BEDF是菱形,请给出证明.
16.如图,△AOB中,OA=OB=6,将△AOB绕点O逆时针旋转得到△COD.OC与AB交于点G,CD分别交OB、AB于点E、F.
(1)∠A与∠D的数量关系是:∠A______∠D;
(2)求证:△AOG≌△DOE;
(3)当A,O,D三点共线时,恰好OB⊥CD,求此时CD的长.
17.如图1,在△ABC中,∠BAC=90°,AB=AC,点D在边AC上,CD⊥DE,且CD=DE,连接BE,取BE的中点F,连接DF.
(1)请直接写出∠ADF的度数及线段AD与DF的数量关系;
(2)将图1中的△CDE绕点C按逆时针旋转,
①如图2,(1)中∠ADF的度数及线段AD与DF的数量关系是否仍然成立?请说明理由;
②如图3,连接AF,若AC=3,CD=1,求S△ADF的取值范围.
18.如图,已知等边中,点D、E、F分别为边、、的中点,M为直线上一动点,为等边三角形(点M的位置改变时,也随之整体移动).
(1)如图1,当点M在点B左侧时,请你连结,并判断与有怎样的数量关系?点F是否在直线上?请写出结论,并说明理由;
(2)如图2,当点M在上时,其它条件不变,(1)的结论中与的数量关系是否仍然成立?若成立,请利用图2证明;若不成立,请说明理由;
(3)如图3,若点M在点C右侧时,请你判断(1)的结论中与的数量关系是否仍然成立?若成立,请直接写出结论:若不成立,请说明理由.
参考答案:
1.
【分析】(1)根据直角三角形斜边上的中线等于斜边的一半,即可求解;
(2)①根据等腰直角三角形的性质,旋转的性质可得是等腰直角三角形,如图所示,延长交于,连接,可证,,可得是等腰直角三角形,根据等腰直角三角形的性质即可求解;②根据上述证明,分别求出的值,如图所示,过点作于,根据勾股定理可求出的值,由此即可求解.
【详解】(1)证明:∵,
∴是直角三角形,
∵点是的中点,
∴,
∵,
∴,
∵点是的中点,
∴,
∴.
(2)解:①根据题意可知,在图①中,
∵,,
∴,
∵,
∴,
∴,
∴,即是等腰直角三角形,
如图所示,延长交于,连接,
由旋转知,,,
∴,
∵点是的中点,
∴,
∵,
∴,
∴,,
∵,
∵,
∴,
∴,,
∴,
∴是等腰直角三角形,
∵,
∴,;
②在中,,
∴,,
在图①中,点是的中点,
∴,
∵是等腰直角三角形,
∴,
由①知,,
∴,
∴,
在中,,
∵,
∵是的斜边上的中线,
∴,
∴,
如图所示,过点作于,
∴,
在中,根据勾股定理得,,
∴.
2.
【分析】(1)根据旋转的性质可知,进而可证,即可得结论;②要使成立,则旋转后点E的对应点和点F,点D在同一直线上,则;
(2)同(1)逻辑将绕点A逆时针旋转至,证,再通过勾股定理即可求解;
【详解】(1)解:①根据旋转的性质可知,
∴,
∵,
∵,
∵
∴,
∴,
在和中,
∵,
∴,
∴,
∵,
∴.
②当时,.
把绕点A逆时针旋转,
∵,,
∴旋转后与重合,
∵,
∴旋转后点E的对应点和点F,点D在同一直线上,
同①理得.
(2)如图,把绕点A逆时针旋转至,使与重合,
∴,
∴,
∵,,
∴,
同(1)理可证,
∴
∵,
∴,
∵,,
∴,
∴,
∴,
∴,即,
∴,
∴.
3.
【分析】(1)根据已知条件和全等三角形的判定定理,得出△BAD△CAE;
(2)连接CE,根据旋转可得AD=AE,结合BAD=CAE,AB=AC得BADCAE(SAS),进而可证+=直接转换得出答案即可;
(3)作AE⊥AD,使AE=AD,连接CE,DE,先利用SAS证明△BAD△CAE,得到CE=3,在Rt△CDE中,利用勾股定理可求出DE=,最后在RT△ADE中,利用勾股定理可求出AD=2,
【详解】解:(1)BC=DC+EC,
∵∠BAC=∠DAE=90°,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,即∠BAD=∠CAE,
在△BAD和△CAE中,
∴△BAD△CAE,
∴BD=CE,
∴BC=BD+CD=EC+CD,
即:BC=DC+EC;
(2)+=
连接CE
∵BAC=DAE=90° ,
∴BAD=CAE,
∵ AB=AC,
根据旋转可得AD=AE,
∴
∴BADCAE(SAS),
∴ACE=B,
∴DCE=BAC+ACE=BAC+B=90°,
∴+=,
在Rt△ADE中,AD=AE,,
∴,
∴+=.
(3)AD=2,
作AE⊥AD,使AE=AD,连接CE,DE,
∵∠BAC+∠CAD=∠DAE+∠CAD,
即∠BAD=∠CAE,
在△BAD与△CAE中,
∴△BAD△CAE(SAS),
∴BD=CE=3,
∵∠ADC=45°,∠EDA=45°,
∴∠EDC=90°,
∴DE=,
∵∠DAE=90°,
∴AD+AE=DE,
∴AD=2.
4.
【分析】(1)由旋转的性质得到∠BAE=∠DAG,由正方形的性质得到AB=AD,AE=AG,然后依据SAS可证明△ABE≌△ADG,然后依据全等三角形的性质进行证明即可;
(2)画出图形,过即可F点作FH⊥GC于H点,证明△ABE≌△GHF(AAS),由此得到HF=BE=GD=GH+HD=CD+HD=HC,进而证明△HCF为等腰直角三角形即可求解;
(3)连接GE、BG,延长AD交GE与H.当α=45°时,可证明△AHE为等腰直角三角形,然后可求得AH和HE的长,然后依据等腰三角形三线合一的性质可得到EG=2HE,最后在△BEG中,利用面积法可求得点G到BE的距离.
【详解】(1)证明:由旋转的性质可知:∠BAE=∠DAG,由正方形的性质可知:AB=AD,AE=AG,
∵在△ABE和△ADG中,,
∴△ABE≌△ADG(SAS),
∴BE=DG.
(2)解:当点在射线上时,连接,如下图所示:
过F点作FH⊥GC于H点,
∴∠FGH+∠DGA=∠FGA=90°,
∠BAE+∠BEA=90°,
由(1)知:∠BEA=∠DGA,
∴∠FGH=∠BAE,
又AE=GF,∠B=∠GHF=90°,
∴△ABE≌△GHF(AAS),
∴GH=AB=CD,
由(1)知:GD=BE,
∴HF=BE=GD=GH+HD=CD+HD=HC,
∴△HCF为等腰直角三角形,
∴∠HCF=45°,
即∠FCD=45°.
(3)解:连接GE、BG,延长AD交GE与H,如下图所示:
当∠GAD=α=45°时,则∠BAE=45°.
∵∠BAD=∠EAG=90°.
∴∠EAH=∠GAH=45°.
又∵AE=AG,
∴AH⊥GE.
又∵AH⊥AB,∠EAH=45°,
∴△AHE为等腰直角三角形.
∴EH=AH=AE=4,
∴EG=2EH=8,DH=AH-AD=4-2=2,
∴,
∴S△BEG= S△BEA==EG•AH=×8×4=16,
设点G到BE的距离为h,
∴S△BEG=BE×h=16,代入,
∴,
∴点到的距离为.
5.(1)∠AFD=∠DCA(或相等);(2)∠AFD=∠DCA(或成立);(3)BO⊥AD.
【分析】(1)要证∠AFD=∠DCA,只需证△ABC≌△DEF即可;
(2)结论成立,先证△ABC≌△DEF,再证△ABF≌△DEC,得∠BAF=∠EDC,推出∠AFD=∠DCA;
(3)BO⊥AD,由△ABC≌△DEF得BA=BD,点B在AD的垂直平分线上,且∠BAD=∠BDA,继而证得∠OAD=∠ODA,OA=OD,点O在AD的垂直平分线上,即BO⊥AD.
【详解】(1)∠AFD=∠DCA.证明如下:
∵AB=DE,BC=EF,∠ABC=∠DEF,∴△ABC≌△DEF,∴∠ACB=∠DFE,∴∠AFD=∠DCA;
(2)∠AFD=∠DCA(或成立),理由如下:
由(1)得:△ABC≌△DEF,∴AB=DE,BC=EF,∠ABC=∠DEF,∠BAC=∠EDF,∴∠ABC﹣∠CBF=∠DEF﹣∠CBF,∴∠ABF=∠DEC.
在△ABF和△DEC中,∵,∴△ABF≌△DEC(SAS),∠BAF=∠EDC,∴∠BAC﹣∠BAF=∠EDF﹣∠EDC,即∠FAC=∠CDF.
∵∠AOD=∠FAC+∠AFD=∠CDF+∠DCA,∴∠AFD=∠DCA;
(3)如图,BO⊥AD.证明如下:
由△ABC≌△DEF,点B与点E重合,得∠BAC=∠BDF,BA=BD,∴点B在AD的垂直平分线上,且∠BAD=∠BDA.
∵∠OAD=∠BAD﹣∠BAC,∠ODA=∠BDA﹣∠BDF,∴∠OAD=∠ODA,∴OA=OD,点O在AD的垂直平分线上,∴直线BO是AD的垂直平分线,即BO⊥AD.
【点睛】本题综合考查全等三角形、等腰三角形的判定与性质、线段垂直平分线的判定定理和旋转的有关知识.注意对三角形全等知识的综合应用.
6.(1)全等的三角形有:△CBD≌△CA 1 F或△AEF≌△B 1 ED或△ACD≌△B 1 CF等;证明见解析;(2)α=30° ;(3)
【分析】(1)依据全等三角形的判定,可找出全等的三角形有:△CBD≌△CA1F或△AEF≌△B1ED或△ACD≌△B1CF等.由旋转的意义可证∠A1CF=∠BCD,A1C=BC,∠A1=∠CBD=45°,所以△CBD≌△CA1F.
(2)当△BBD是等腰三角形时,要分别讨论B1B=B1D、BB1=BD、B1D=DB三种情况,第一,三种情况不成立,只有第二种情况成立,求得α=30°.
(3)作DG⊥BC于G,在直角三角形CDG和直角三角形DGB中,由三角函数即可求得BD的长.
【详解】(1)全等的三角形有:△CBD≌△CA 1 F或△AEF≌△B 1 ED或△ACD≌△B 1 CF等;
以说明△CBD≌△CA 1 F为例:
理由:∵∠ACB 1 +∠A 1 CF=∠ACB 1 +∠BCD=90°
∴∠A 1 CF=∠BCD
∵A 1 C=BC
∴∠A 1 =∠CBD=45°
∴△CBD≌△CA 1 F;
(2)在△CBB 1 中 ∵CB=CB 1
∴∠CBB 1 =∠CB 1 B=(180°-α)
又△ABC是等腰直角三角形
∴∠ABC=45°
①若B 1 B=B 1 D,则∠B 1 DB=∠B 1 BD
∵∠B 1 DB=45°+α
∠B 1 BD=∠CBB 1 -45°=(180°-α)-45°=45°-α
∴45°+α=45°-α
∴α=0°(舍去);
②∵∠BB 1 C=∠B 1 BC>∠B 1 BD,
∴BD>B 1 D,即BD≠B 1 D;
③若BB 1 =BD,则∠BDB 1 =∠BB 1 D,即45°+α=(180°-α),α=30°
由①②③可知,当△BB 1 D为等腰三角形时,α=30°;
(3)作DG⊥BC于G,设CG=x
在Rt△CDG中,∠DCG=α=60°,
∴DG=xtan60°=,
在Rt△DGB中,∠DBG=45°,
∴BG=GD=,
∵AC=BD=1,
∴x+=1
∴x=,
∴DB=
7.
【分析】(1)利用证明,即可得出答案;
(2)①由三角形内角和定理知,再利用角度之间的转化对进行转化,,从而解决问题;
②延长到,使,连接,,得出四边形为平行四边形,则且,再利用证明,得.
【详解】(1)解:,
证明:是等边三角形,
,,
将线段绕点顺时针旋转得到,
,,
,
,
,
;
(2)解:①当时,
则,
,
,
,
故答案为:;
②,理由如下:
延长到,使,连接,,
为的中点,
,
四边形为平行四边形,
且,
,,
又,
,
,
又,,
,
,
又为正三角形,
,
.
8.
【分析】(1)连接,先根据“”证明,得出,再证明,即可得出结论;
(2)连接,先说明,然后根据“”证明,得出,再证明,即可得出结论;
(3)过点C作,根据,得出点E总是在直线上,过点作于点E,此时最小,根据直角三角形的性质,求出此时的长即可.
【详解】(1)解:;理由如下:
连接,如图所示:
根据旋转可知,,,
∵,
∴,,
∴,
在和中,
∴,
∴,
∴,
在与中,
∴,
∴.
(2)解:成立,理由如下:
连接,如图所示:
根据旋转可知,,,
∵,
∴,,
∴,
在和中,
∴,
∴,
∴,
在与中,
∴,
∴.
(3)解:过点C作,
根据解析(2)可知,,
∴点E总是在直线上,
过点作于点E,此时最小,
∵,,
∴为等边三角形,
∴,,
∴,
∵
∴,
∴.
故答案为:.
9.(1),,;
(2);
(3)或或.
【分析】(1)由旋转的性质得,,,,由勾股定理求出的长,判断出与x轴平行,进而可得点,点的坐标;
(2)作轴于H,如图2,利用旋转的性质得,,则,再在中利用含30度的直角三角形的性质和勾股定理计算出和的长,进而可得点的坐标;
(3)分三种情况:①当、为平行四边形的边时,连接,交于点P,根据,,利用中点坐标公式求出点P的坐标,进而可得点D的坐标;②当为对角线时,③当为对角线时,同理求解即可.
【详解】(1)解:∵点,点,
∴,,
∴,
∵把绕点B逆时针旋转得,
∴,,
∴,
∵,,,
∴与x轴平行,
∴,
∵是直角三角形,,
∴的坐标为,
综上,的坐标为,的坐标为,的长为,
故答案为:,,;
(2)解:作轴于H,如图2,
∵绕点B逆时针旋转得,
∴,,
∴,
在中,,
∴,,
∴,
∴点的坐标为;
(3)解:分三种情况:
①当、为平行四边形的边时,如图,
连接,交于点P,
∵四边形是平行四边形,
∴,,
∵点,点的坐标为,
∴,
∵点,
∴点D的坐标为;
②当为对角线时,如图,
同理可得,点D的坐标为;
③当为对角线时,如图,
同理可得,点D的坐标为;
.
综上,点D的坐标为或或.
10.
【分析】(1)根据题意得出,证明得出,继而得出,根据三线合一即可得证;
(2)在上取一点,使得.连接交于点,证明,四边形是平行四边形,进而根据平行四边形的性质即可得证;
(3)方法同(2)证明即可得证.
【详解】(1)证明:如图2中,
是等边三角形,
,,
点与重合,
,,重合,
,
,
,
,
,,
,
,
,
,
,即为中点;
(2)解:如图1中,在上取一点,使得.连接交于点.
是等边三角形,
,,
,
,
,
,
,
,
,
,
四边形是平行四边形,
,
,,
,
;
(3)结论成立.
理由:如图3中,在上取一点,使得.连接交于点.
是等边三角形,
,,
,
,
,
,
,
,
,
,
四边形是平行四边形,
,
,,
,
.
11.
【分析】(1)由平行四边形的性质及,可得,再由已知可得结论;
(2)过点作于点E,交于点,则由平行四边形的性质得,证明,可得,从而由已知面积关系可得,由勾股定理可求得的长,从而可求得平行四边形的面积;
(3)连接,由旋转性质易得,则可得,设,由旋转及勾股定理可分别求得、、,进而可求得,由勾股定理求得,则最后可求得结果.
【详解】(1)∵四边形是平行四边形,
∴,
∵,
∴,
即,
∵,
∴,
∴;
(2)过点作于点E,交于点,如图,
∴,
∵四边形是平行四边形,
∴,,
∴,
即,
∴,
∵,
∴,
在与中,
,
∴,
∴,
∵,
即,
∴,
∴,
在中,由勾股定理得:,
即,
解得:;
∴,
∴平行四边形的面积为;;
(3)连接,如图,
由旋转性质得:,,,,
∵,
∴,即,
∵,
∴,
即,
∴,
∵,
∴,
∴,
∴,
设,则,,
在中,由勾股定理得,
∵,,
∴,
在中,由勾股定理得:,
∴,
在中,由勾股定理得,
∴;
故答案为:.
12.(1)等边三角形
(2)∠BCE=2∠BAC
(3)点D在运动过程中,△DEC的周长存在最小值,最小值为4+2,此时△DEC的面积为.
【分析】(1)根据旋转的性质得到AD=AE,∠DAE=60°,根据等边三角形的判定定理解答;
(2)证明△ABD≌△ACE,根据全等三角形的性质得到∠B=∠ACE=60°,结合图形计算即可;
(3)根据△ABD≌△ACE得到CE=BD,根据垂线段最短解答.
【详解】(1)解:由旋转变换的性质可知,AD=AE,∠DAE=60°,
∴△ADE是等边三角形,
故答案为:等边三角形;
(2)解:∠BCE=2∠BAC,理由如下:
证明:由旋转的性质可知,∠DAE=60°,AD=AE,
∵△ABC是等边三角形,
∴AB=AC=BC,∠BAC=∠ACB=60°,
∴∠BAC=∠DAE=60°,
∴∠BAC+∠DAC=∠DAE+∠DAC,即∠BAD=∠CAE,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS),
∴∠B=∠ACE=60°,
∴∠BCE=∠ACB+∠ACE=120°,
∴∠BCE=2∠BAC;
(3)解:点D在运动过程中,△DEC的周长存在最小值,最小值为4+2,此时△DEC的面积为.
理由如下:∵△ABD≌△ACE,
∴CE=BD,
则△DEC的周长=DE+CE+DC=BD+CD+DE=BC+DE,
∴当DE最小时,△DEC的周长最小,
∵△ADE是等边三角形,
∴AD=DE,
由垂线段最短可知,当AD⊥BC时,△DEC的周长最小,
∵△ABC是等边三角形,
∴AB=AC=BC=4,
∴BD=DC=2,
∴AD==2,
∵△ADE为等边三角形,
∴DE=AD,∠ADE=60°,
∴△DEC的周长的最小值为4+2.
过点E作EG⊥BC并交BC延长线于点G,如图:
∵∠ADE=60°,
∴∠EDG=30°,
∴EG=DE=,
此时△DEC的面积=DC×EG=.
13.(1)①AC=BD;②35°
(2)①BD=AC,理由见解析;②90°
(3)OD=OA或OD=OA
【分析】(1)①由旋转的性质结合题意利用“SAS”易证,即得出AC=BD;②设线段BD和AO交于点P,由全等的性质可知,再根据对顶角相等得出,从而即可得出;
(2)①由(1)①同理可证,即得出AC=BD;②由(1)②同理可求∠AMB=90°;
(3)分类讨论:①当点C在点B上方时,由(1)同理易证,即得出,AC=BD,从而证明.设OD=x,OA=y,由等腰直角三角形的性质、勾股定理和含30度角的直角三角形的性质可得出,,,从而得出关于x,y的等式,最后整理即可得出OD和OA的关系;②当点C在点B下方时,同理求解即可.
【详解】(1)①由旋转可知OC=OD,∠COD=35°
∴∠COD=∠AOB=35°,
∴∠COD+∠AOD =∠AOB+∠AOD,即∠AOC=∠BOD.
又∵ OA=OB,
∴(SAS),
∴AC=BD;
②如图,设线段BD和AO交于点P,
∵,
∴.
又∵,
∴,即.
故答案为:AC=BD ,35°;
(2)①由(1)①同理可证,即得出AC=BD;
②由(1)②同理可求∠AMB=90°;
(3)分类讨论:①当点C在点B上方时,如图3所示,
∠AOB=∠COD=90°,OA=OB,OC=OD,∠CAB=30°,
∵C,M重合,
∴B,C,D共线.
设OD=x,OA=y,
则,.
根据(1)同理可证,
∴,AC=BD,
∴.
∴,
∴.
∵,即
∴
∴,即;
②当点C在点B下方时,如图4,
同上易求得OD=OA.
综上所述,OD=OA或OD=OA.
14.
【分析】(1)由正方形的性质和△APB≌△AND,推出∠PAM=∠NAM=45°,利用SAS即可证明△APM≌△ANM;
(2)由正方形的性质和△APB≌△AND,推出∠BPM=∠ABP+∠ABD=90°,再由(1)的结论得到PM=MN,根据勾股定理即可证明;
(3)将△ABM绕点A逆时针旋转90°,得到△,则△AMN≌△,利用全等三角形的性质可得出=MN,由∠C=90°,∠CMN=45°可得出CM=CN,设BM=a,DN=b,CM=c,则AD=a+c,CD=b+c,进而可得出=a-b,NF=b+a,在Rt△中,利用勾股定理可求出,进而可得出.
【详解】(1)证明:∵四边形ABCD是正方形,
∴∠BAD=90°,
∵∠EAF=45°.
∴∠BAM+∠NAD=45°,
∵△APB≌△AND,
∴PA=NA,∠PAB=∠NAD,
∴∠PAB+∠BAM=45°,
∴∠PAM=∠NAM=45°,
在△APM和△ANM中,,
∴△APM≌△ANM(SAS);
(2)证明:∵四边形ABCD是正方形,
∴AB=AD,∠ABD=∠ADB=45°,
∵△APB≌△AND,
∴PB=ND,∠ABP=∠ADB=45°,
∴∠BPM=∠ABP+∠ABD=90°,
∴,
∵△APM≌△ANM,
∴PM=MN,
∴;
(3)解:.理由如下:
将△ABM绕点A逆时针旋转90°,得到△.如图:
过点作⊥CD于F,连接,
同(1)可证△AMN≌△,
∴=MN.
∵∠C=90°,∠CMN=45°,
∴CM=CN.
设BM=a,DN=b,CM=c,则AD=a+c,CD=b+c,
∴=AD-=AD-AB=a+c-(b+c)=a-b,
NF=DN+DF=DN+=DN+BM=b+a.
在Rt△中,,
∴.
【点睛】本题考查了旋转的性质、全等三角形的判定与性质、等腰直角三角形以及勾股定理,解题的关键是:(1)利用SAS即可证明△APM≌△ANM;(2)证明∠BPM=90°,利用勾股定理求解;(3)通过构造直角三角形,利用勾股定理找出.
15.(1)见解析
(2)见解析
(3)45°,见解析
【分析】(1)根据平行四边形的性质得,根据已知条件可得,根据两组对边分别平行的四边形是平行四边证明即可;
(2)通过证明△AOF≌△COE(ASA).即可得证;
(3)根据题意与勾股定理求得,根据平行四边形的性质可得,得到,结合菱形的性质和判定求解.
【详解】(1)证明:如图,
∵平行四边形ABCD中,ADBC,
∴AFBE,
∵AB⊥AC,
∴∠BAC=90°,
又∵旋转角为90°时,∠AOF=90°,
∴∠BAC=∠AOF,
∴ABEF,
∴四边形ABEF是平行四边形.
(2)证明:∵四边形ABCD是平行四边形,
∴OA=OC,ADBC,
∴∠OAF=∠OCE,
∵∠AOF=∠COE,
∴△AOF≌△COE(ASA).
∴AF=CE.
∴在旋转过程中,线段AF与EC总保持相等.
(3)当AC绕点O顺时针旋转45度时,四边形BEDF是菱形.
理由如下:
由(2)知:AF=CE,
∵四边形ABCD是平行四边形,
∴ADBC,AD=BC,
∴DF=BE,DFBE,
∴四边形BEDF是平行四边形.
如图:
∵AB⊥AC,AB=1,BC=,
∴,
∵四边形ABCD是平行四边形,
∴AO=AC=1,
∴AO=AB,
∵AB⊥AC,
∴∠AOB=45°
∵AC绕点O顺时针旋转45度,
∴∠AOF=45°,
∴∠BOF=90°,
∴EF⊥BD.
∴四边形BEDF是菱形.
16.
【分析】(1)根据旋转性质及等腰三角形性质即可得答案;
(2)由旋转性质知∠AOB=∠DOC,可证得∠AOG=∠DOE,结合OA=OB及(1)中结论,得证;
(3)分两种情况讨论,设∠A=x°,先利用三角形内角和求出x的值,再借助勾股定理求出CD的长度即可.
【详解】(1)解:由旋转知,∠A=∠C,∠B=∠D,
∵OA=OB,
∴OC=OD,∠A=∠B=∠C=∠D
∴∠A=∠D,
故答案为:=.
(2)证明:由旋转知,OA=OC,OB=OD,∠AOB=∠COD,
∴∠AOB-∠BOC=∠COD-∠BOC,
即∠AOG=∠DOE,
∵OA=OB,
∴OA=OB=OC=OD,
又∵∠A=∠D,
∴△AOG≌△DOE.
(3)解:分两种情况讨论,
①如图所示,
设∠A=∠B=∠C=∠D=x°,则∠DOB=2x°,
∵OB⊥CD,
∴∠OED=90°,
∴x+2x=90°,
解得:x=30,
即∠D=30°,
在Rt△ODE中,OE=3,由勾股定理得:DE=,
∵OC=OD,OE⊥CD,
∴CD=2DE=.
②当D与A重合时,如图所示,
同理,得:CD=.
综上所述,当A,O,D三点共线时,OB⊥CD,此时CD的长为.
17.
【分析】(1)延长DF交AB于H,连接AF,先证明△DEF≌△HBF,得BH=CD,再证明△ADH为等腰直角三角形,利用三线合一及等腰直角三角形边的关系即可得到结论;
(2)①过B作DE的平行线交DF延长线于H,连接AH、AF,先证明△DEF≌△HBF,延长ED交BC于M,再证明∠ACD=∠ABH,得△ACD≌△ABH,得AD=AH,等量代换可得∠DAH=90°,即△ADH为等腰直角三角形,利用三线合一及等腰直角三角形边的关系即可得到结论;
②先确定D点的轨迹,求出AD的最大值和最小值,代入S△ADF=求解即可.
【详解】(1)解:∠ADF=45°,AD=DF,理由如下:
延长DF交AB于H,连接AF,
∵∠EDC=∠BAC=90°,
∴DE∥AB,
∴∠ABF=∠FED,
∵F是BE中点,
∴BF=EF,
又∠BFH=∠DFE,
∴△DEF≌△HBF,
∴BH=DE,HF=FD,
∵DE=CD,AB=AC,
∴BH=CD,AH=AD,
∴△ADH为等腰直角三角形,
∴∠ADF=45°,
又HF=FD,
∴AF⊥DH,
∴∠FAD=∠ADF=45°,
即△ADF为等腰直角三角形,
∴AD=DF;
(2)解:①结论仍然成立,∠ADF=45°,AD=DF,理由如下:
过B作DE的平行线交DF延长线于H,连接AH、AF,如图所示,
则∠FED=∠FBH,∠FHB=∠EFD,
∵F是BE中点,
∴BF=EF,
∴△DEF≌△HBF,
∴BH=DE,HF=FD,
∵DE=CD,
∴BH=CD,
延长ED交BC于M,
∵BH∥EM,∠EDC=90°,
∴∠HBC+∠DCB=∠DMC+∠DCB=90°,
又∵AB=AC,∠BAC=90°,
∴∠ABC=45°,
∴∠HBA+∠DCB=45°,
∵∠ACD+∠DCB=45°,
∴∠HBA=∠ACD,
∴△ACD≌△ABH,
∴AD=AH,∠BAH=∠CAD,
∴∠CAD+∠DAB=∠BAH+∠DAB=90°,
即∠HAD=90°,
∴∠ADH=45°,
∵HF=DF,
∴AF⊥DF,即△ADF为等腰直角三角形,
∴AD=DF.
②由①知,S△ADF=DF2=AD2,
由旋转知,当A、C、D共线时,且D在A、C之间时,AD取最小值为3-1=2,
当A、C、D共线时,且C在A、D之间时,AD取最大值为3+1=4,
∴1≤S△ADF≤4.
【点睛】本题考查了等腰直角三角形性质及判定、全等三角形判定及性质、勾股定理等知识点.构造全等三角形及将面积的最值转化为线段的最值是解题关键.遇到题干中有“中点”时,采用平行线构造出对顶三角形全等是常用辅助线.
18.(1)相等,在,理由见解析;(2)成立,证明见解析;(3)成立.
【分析】(1)连接DE、DF、EF,NF,根据等边三角形的性质和三角形中位线的性质,先证得△DBF是等边三角形,可得△DMB≌△DNF,可得∠DBM=∠DFN,从而得到∠NFD+∠DFE=180°,再由△DMN是等边三角形,从而证得△DMF ≌△DNE,得到EN=MF,即可求证;
(2)连接DF,NF, EF,等边三角形的性质,可证得△DMB≌△DNF,得到BM=FN,∠DFN=∠FDB=60°,从而NF∥BD,再由EF是△ABC的中位线,可得EF∥BD,从而F在直线NE上,即可求证;
(3)连接DF、DE,EF,根据等边三角形的性质和三角形中位线的性质,可得△DBF是等边三角形,从而证得△DNE≌△DMF,即可求证.
【详解】解:(1)EN=MF,点F在直线NE上,理由如下:
如图1,连接DE、DF、EF,NF,
∵△ABC是等边三角形,
∴AB=AC=BC, ,
又∵点D、E、F分别为边、、的中点,
∴DE、DF、EF为等边△ABC的中位线,
,
∴DE=DF=EF,
∴∠FDE=∠DFE=60°
∵D、F分别是AB、BC的中点,
∴ ,
∴△DBF是等边三角形,
∴∠BDF=60°,
∵△DMN是等边三角形,
∴∠MDN=60°,DM=DN,
∴∠MDN=∠BDF=60°,DB=DF,
∴∠MDN-∠BDN=∠BDF-∠BDN,即∠MDB=∠NDF,
在△DMB和△DNF中,
∵DM=DN,∠MDB=∠NDF,DB=DF,
∴△DMB≌△DNF,
∴∠DBM=∠DFN,
∵∠ABC=60°,
∴∠DBM=120°,
∴∠NFD=120°,
∴∠NFD+∠DFE=120°+60°=180°,
∴N、F、E三点共线,
∴F在直线NE上;
∵△DMN是等边三角形,
∴∠MDN=60°,DM=DN,
∴∠FDE+∠NDF=∠MDN+∠NDF,
∴∠MDF=∠NDE,
在△DMF和△DNE中,
∵DF=DE,∠MDF=∠NDE,DM=DN,
∴△DMF ≌△DNE,
∴MF=NE,
(2)成立,理由如下:
如图2,连接DF,NF,EF,
∵△ABC是等边三角形且D、F分别是AB、BC的中点,
∴ , ,
∴△DBF是等边三角形,
∴∠BDF=∠DBF=60°,
∵△DMN是等边三角形,
∴∠MDN=60°,DM=DN,
∴∠MDN=∠BDF=60°,DB=DF,
∴∠MDN-∠FDM=∠BDF-∠FDM,即∠MDB=∠NDF,
在△DMB和△DNF中,
∵DM=DN,∠MDB=∠NDF,DB=DF,
∴△DMB≌△DNF,
∴∠DBM=∠DFN=60°,BM=FN,
∴∠DFN=∠FDB=60°,
∴NF∥BD,
∵E,F分别为边AC,BC的中点,
∴EF是△ABC的中位线, ,
∴EF∥BD, ,
∴F在直线NE上,BF=EF,
∴MF=EN;
(3)MF与EN相等的结论仍然成立,理由如下:
如图3,连接DF、DE,EF,
∵△ABC是等边三角形,
∴AB=AC=BC,
又∵点D、E、F分别为边、、的中点,
∴DE、DF、EF为等边△ABC的中位线,
,
∴DE=DF=EF,
∴△DEF是等边三角形,
∴∠FDE=60°,
∵△DMN是等边三角形,
∴∠MDN=∠FDE=60°,DM=DN,
∴∠EDM+∠NDE=∠EDM+∠FDM,
∴∠NDE=∠FDM,
在△DNE和△DMF中,
∵DE=DF,∠NDE=∠FDM,DN=DM,
△DNE≌△DMF,
∴MF=NE.
【期中复习】人教版 初中数学九年级上册 期末专题复习 二次函数(面积问题)压轴题专题训练(含解析): 这是一份【期中复习】人教版 初中数学九年级上册 期末专题复习 二次函数(面积问题)压轴题专题训练(含解析),共61页。试卷主要包含了抛物线与轴交于、两点等内容,欢迎下载使用。
【期中复习】人教版 初中数学九年级上册 期末专题复习 二次函数压轴题专题训练(含详解): 这是一份【期中复习】人教版 初中数学九年级上册 期末专题复习 二次函数压轴题专题训练(含详解),共55页。试卷主要包含了综合与探究等内容,欢迎下载使用。
【期中复习】人教版 初中数学九年级上册 期末专题复习 二次函数压轴题专题训练(含解析): 这是一份【期中复习】人教版 初中数学九年级上册 期末专题复习 二次函数压轴题专题训练(含解析),共59页。试卷主要包含了已知二次函数,如图,抛物线与直线交于点和点B,已知抛物线的顶点为与轴交于等内容,欢迎下载使用。












