



- 一元一次方程知识串讲-2023-2024学年七年级数学上学期期末考点预测(人教版)课件PPT 试卷 0 次下载
- 几何图形初步知识串讲-2023-2024学年七年级数学上学期期末考点预测(人教版)课件PPT 试卷 1 次下载
- 清单04 几何图形初步(14个考点梳理+题型解读+核心素养提升+中考聚焦)-2023-2024学年七年级数学上学期期末考点预测(人教版) 试卷 1 次下载
- 预测01数轴上动点问题的答题技巧与方法(50题专练)-2023-2024学年七年级数学上学期期末考点预测(人教版) 试卷 1 次下载
- 预测02有理数与整式加减综合之数轴上动点、绝对值问题、探究规律、新定义(解答60题专练)-2023-2024学年七年级数学上学期期末考点预测(人教版) 试卷 0 次下载
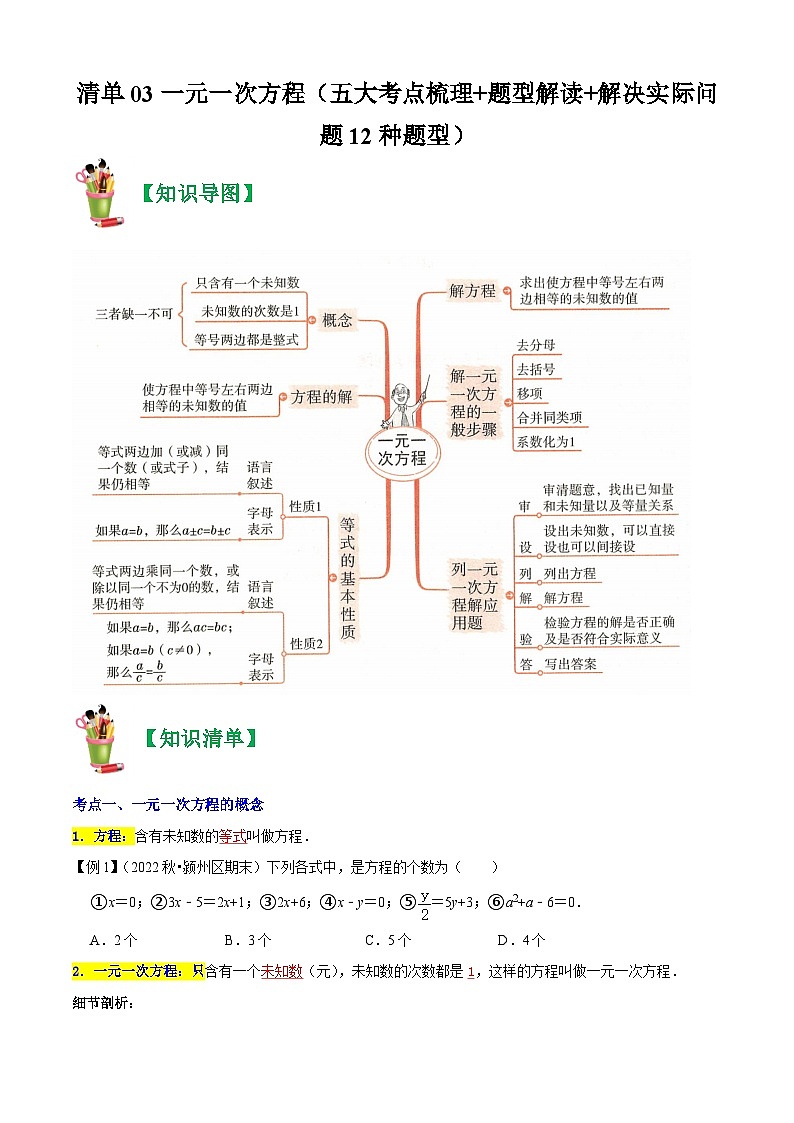
清单03 一元一次方程(五大考点梳理+题型解读+解决实际问题12种题型)-2023-2024学年七年级数学上学期期末考点预测(人教版)
展开【知识清单】
考点一、一元一次方程的概念
1.方程:含有未知数的等式叫做方程.
【例1】(2022秋•颍州区期末)下列各式中,是方程的个数为( )
①x=0;②3x﹣5=2x+1;③2x+6;④x﹣y=0;⑤=5y+3;⑥a2+a﹣6=0.
A.2个B.3个C.5个D.4个
2.一元一次方程:只含有一个未知数(元),未知数的次数都是1,这样的方程叫做一元一次方程.
细节剖析:
判断是否为一元一次方程,应看是否满足:
①只含有一个未知数,未知数的次数为1;
②未知数所在的式子是整式,即分母中不含未知数.
【例2】(2022秋•汉台区期末)已知(m﹣3)x|m|﹣2=18是关于x的一元一次方程,则( )
A.m=2B.m=﹣3C.m=±3D.m=1
3.方程的解:使方程的左、右两边相等的未知数的值叫做这个方程的解.
【例3】(2023春•蒸湘区校级期末)若x=﹣1是方程2x+m﹣6=0的解,则m的值是( )
A.﹣4B.4C.﹣8D.8
【变式】(2022秋•宁阳县期末)若一元一次方程ax+b=0的解是x=1,则a,b的关系为( )
A.相等B.互为相反数
C.互为倒数D.互为负倒数
4.解方程:求方程的解的过程叫做解方程.
考点二、等式的性质与去括号法则
1.等式的性质:
等式的性质1:等式两边加(或减)同一个数(或式子),结果仍相等.
等式的性质2:等式两边乘同一个数,或除以同一个不为0的数,结果仍相等.
【例4】(2022秋•雅安期末)下列等式变形错误的是( )
A.若,则x﹣1=2x
B.若x﹣1=3,则x=4
C.若x﹣3=y﹣3,则x﹣y=0
D.若3x+4=2x,则3x﹣2x=﹣4
2.合并法则:合并时,把系数相加(减)作为结果的系数,字母和字母的指数保持不变.
3.去括号法则:
(1)括号外的因数是正数,去括号后各项的符号与原括号内相应各项的符号相同.
(2)括号外的因数是负数,去括号后各项的符号与原括号内相应各项的符号相反.
考点三、一元一次方程的解法
解一元一次方程的一般步骤:
(1)去分母:在方程两边同乘以各分母的最小公倍数.
(2)去括号:依据乘法分配律和去括号法则,先去小括号,再去中括号,最后去大括号.
(3)移项:把含有未知数的项移到方程一边,常数项移到方程另一边.
(4)合并:逆用乘法分配律,分别合并含有未知数的项及常数项,把方程化为ax=b(a≠0)的形式.
(5)系数化为1:方程两边同除以未知数的系数得到方程的解(a≠0).
(6)检验:把方程的解代入原方程,若方程左右两边的值相等,则是方程的解;若方程左右两边的值不相等,则不是方程的解.
【例5】(2022秋•东宝区期末)解方程:
(1)4﹣2x=﹣3(2﹣x); (2).
考点四、列方程解应用题的步骤:
①审:审题,分析题中已知什么,求什么,明确各数量之间关系
②设:设未知数(一般求什么,就设什么为x)
③找:找出能够表示应用题全部意义的一个相等关系
④列:根据这个相等关系列出需要的代数式,进而列出方程
⑤解:解所列出的方程,求出未知数的值
⑥答:检验所求解是否符合题意,写出答案(包括单位名称)
【例6】(2022秋•汇川区期末)如图,已知数轴上有A,B两点,它们分别表示数a,b,且(a+6)2+|b﹣12|=0.
(1)填空:a= ,b= ;
(2)点C以2个单位长度/秒的速度从点A向点B运动,到达点B后停止运动.若点D为AC中点,点E为BC中点,在点C运动过程中,线段DE的长度是否发生改变?若不变,求线段DE的长度,若变化,请说明原因;
(3)在(2)的条件下,点P以1个单位长度/秒的速度同时从原点O向点B运动,P点到达B点后停止运动,问点P运动多少秒后,点P与点C相距2个单位长度?
【例7】(2022秋•秦淮区期末)根据国家发改委实施“阶梯电价”的有关文件要求,某市结合地方实际,决定从2015年5月1日起对居民生活用电实施“阶梯电价”收费,具体收费标准见下表:
2015年5月份,该市居民甲用电100千瓦时,交费60元;居民乙用电200千瓦时,交费125元.
(1)求上表中a、b的值;
(2)实施“阶梯电价”收费以后,该市一户居民月用电多少千瓦时,其当月交费285元?
【例8】.(2022秋•常州期末)列方程解决问题:
小华和妈妈一起玩成语竞猜游戏,商定如下规则:小华猜中1个成语得2分,妈妈猜中1个成语得1分,结果两人一共猜中了30个成语,得分恰好相等.请问小华猜中了几个成语?
考点五、用一元一次方程解决实际问题的常见类型
1.行程问题:路程=速度×时间
2.和差倍分问题:增长量=原有量×增长率
3.利润问题:商品利润=商品售价-商品进价
4.工程问题:工作量=工作效率×工作时间,各部分劳动量之和=总量
5.银行存贷款问题:本息和=本金+利息,利息=本金×利率×期数
6.数字问题:多位数的表示方法:例如:
7.数字问题;
8.分配问题;
9.比赛积分问题;
10.水流航行问题(顺水速度=静水速度+水流速度;逆水速度=静水速度-水流速度).
题型1.配套问题
1.某生产教具的厂家准备生产正方体教具,教具由塑料棒和金属球组成(一条棱用一根塑料棒,一个顶点由一个金属球镶嵌),安排一个车间负责生产这款正方体教具,该车间共有34名工人,每个工人每天可生产塑料棒100根或金属球75个,如果你是车间主任,你会如何分配工人成套生产正方体教具?
2.某车间有62个工人,生产甲、乙两种零件,每人每天平均能生产甲种零件12个或乙种零件23个.已知每3个甲种零件和2个乙种零件配成一套,问应分配多少人生产甲种零件,多少人生产乙种零件,才能使每天生产的这两种零件刚好配套?
题型2.销售问题
销售问题中有四个基本量:成本(进价)、销售价(收入)、利润、利润率。
(1)商品利润=商品售价-商品成本价
(2)商品利润率=×100%
(3)商品销售额=商品销售价×商品销售量
(4)商品的销售利润=(销售价-成本价)×销售量
(5)商品打几折出售,就是按原标价的百分之几十出售,如商品打6折出售,即按原标价的60%出售.
3.小明和父母打算去某火锅店吃火锅,该店在网上出售“25元抵50元的全场通用代金券”(即面值50元的代金券实付25元就能获得),店家规定代金券等同现金使用,一次消费最多可用3张代金券,而且使用代金券的金额不能超过应付总金额.
(1)如果小明一家应付总金额为145元,那么用代金券方式买单,他们最多可以优惠多少元;
(2)小明一家来到火锅店后,发现店家现场还有一个优惠方式:除锅底不打折外,其余菜品全部6折.小明一家点了一份50元的锅底和其他菜品,用餐完毕后,聪明的小明对比两种优惠,选择了现场优惠方式买单,这样比用代金券方式买单还能少付15元.问小明一家实际付了多少元?
题型3储蓄问题
(1)顾客存入银行的钱叫做本金,银行付给顾客的酬金叫利息,本金和利息合称本息和,存入银行的时间叫做期数,利息与本金的比叫做利率。利息的20%付利息税
(2)利息=本金×利率×期数
本息和=本金+利息
利息税=利息×税率(20%)
(3)利润=每个期数内的利息/本金×100%
4.小明一年前存入银行一笔钱,年利率为2.25%,到期共获得本息和为10225元,求小明一年前存入银行的本金是多少元?
5.小丽的妈妈在银行存入5000元,存期一年,到期银行代扣利息税22.5元,求这项储蓄的年利率是多少?(国家规定存款利息的纳税办法是:利息税=利息×20%,储户取款时由银行代扣代收).
题型4.工程问题
在解决有关工作量问题的应用题时,常把整个的工作量看做1,若单独完成需要的时间为 ,则工作效率为
6.在某一城市美化工程招标时,有甲、乙两个工程队投标.经测算:甲队单独完成这项工程需要60天,乙队单独完成这项工程需要90天;若由甲队先做20天,剩下的工程由甲、乙两队合作完成.
(1)甲、乙两队合作多少天?
(2)甲队施工一天需付工程款3.5万元,乙队施工一天需付工程款2万元.若该工程计划在70天内完成,在不超过计划天数的前提下,是由甲队或乙队单独完成该工程省钱?还是由甲乙两队全程合作完成该工程省钱?
题型5.和、差、倍、分问题
1.和、差关系:通过关键词语“多、少、和、差、不足、剩余……”来体现.
2.倍、分关系:通过关键词语“是几倍、增加几倍、增加到几倍、增加百分之几、增长率……”来体现.
3.比例问题:全部数量=各种成分的数量之和.此类题目通常把一份设为x.解题的关键是弄清“倍、分”关系及“和、差”关系.
7.一桶油第一次用去,第二次比第一次多用去40千克,还剩下23千克,原来这桶油有多少千克?
8.甲、乙、丙、丁四人一共做了820个零件,如果把甲做的个数加10个,乙做的个数减去20个,丙做的个数乘以2,丁做的个数除以2,那么四人做的个数正好相等,问乙实际上做了多少个零件?
题型6.数字问题
9.一个两位数,把它的个位数字与十位数字交换位置得到新两位数,原两位数的个位数字比原两位数的十位数字大2,且新两位数与原两位数的和为154,求原两位数是多少?
10.一个正两位数的个位数字是a,十位数字比个位数字大2
(1)请列式表示这个两位数,并化简;
(2)把这个两位数的十位上的数字与个位上的数字交换位置得到一个新的两位数,试说明新两位数与原两位数的和能被22整除.
11.一个两位数,十位数字是个位数字的两倍,将这个两位数的十位数字与个位数字对调后得到的两位数比原来的两位数小27,求这个两位数.
题型7.比例分配问题
比例分配问题解题思路:
1.通常设一份为X
2.通常先用字母表示适当的未知数,并用含有这个字母的代数式表示其他相关的量,再根据题中的相等关系列出方程,然后解这个方程,写出问题的答案
12.甲、乙、丙三人共同出资做生意,甲投资了万元,乙投资了万元,丙投资了万元,年终时,共赚得利润万元,甲、乙、丙三人按比例进行分配,各可以分得多少利润?
13.六年级和七年级分别有192人和133人,现在需要从两个年级选出133人参加“读书节”活动,并且要使六年级,七年级剩余学生数之比为2:1,问应从六年级,七年级各选出多少人?
题型8.比赛积分问题
14.某电视台组织知识竞赛,共设30道选择题,各题分值相同,每题必答.下表记录了3个参赛者的得分情况.
(1)每答对1题得多少分?
(2)参赛者D得54分,他答对了几道题?
15.某次篮球联赛共有十支队伍参赛,部分积分表如下.根据表格提供的信息解答下列问题:
(1)列一元一次方程求出胜一场、负一场各积多少分?
(2)某队的胜场总积分能等于它的负场总积分吗?若能,试求胜场数和负场数;若不能,说出理由.
(3)试就某队的胜场数求出该队的负场总积分是它的胜场总积分的正整数倍的情况?
题型9.日历问题
在某月的月历上,横行上左右相邻的两个数是连续整数,它们的差为1,同一竖列上的两个相邻的数是相差7的整数,根据它们的数量关系可以列方程求解。
16.某公司新研发一种办公室用壁挂式电磁日历,底板是一块长方形磁块,再用31枚圆柱形小铁片标上数字吸附在底板上作为日期,如图1是2007年10月份日历
(1)用长方形和正方形分别圈出相邻的3个数和9个数,若设圈出的数的中心数为a,用含a的整式表示这3个数的和与9个数的和,结果分别为 3a , 9a .
(2)用某种图形圈出相邻的5个数,使这5个数的和能表示成5a的形式,请在图2中画出一个这样的图形.
(3)用平行四边形圈出相邻的四个数,是否存在这样的4个数使得a+b+c+d=114?如果存在就求出来,不存在说明理由.
(4)第一次翻动31枚日历铁片,第二次翻动其中的30枚,第三次翻动其中的29枚,……,第31次只翻动其中的一枚,按这样的方法翻动日历铁片,能否使铁板上所有的31枚铁片原来有数字的一面都朝下,试通过计算证明你的判断.
17.生活与数学.
(1)小明在某月的日历上象图①样圈了2×2个数,若正方形的方框内的四个数的和是44,那么这四个数是 .(直接写出结果)
(2)小莉也在日历上象图②样圈出5个数,呈十字框形,若这五个数之和是60,则中间的数是 .(直接写出结果)
(3)小虎说他在日历上向图③样圈了五个数,算了它们的和是65.你认为小虎计算正确吗?说明理由.
拓展与推广:
若干个偶数按每行8个数排成如图④所示:
(1)写出图④中方框内的9个数的和与中间的数的关系是 .
(2)小明说若用图④中所画的方框去框9个数,其和可以是360,你能求出所框的中间一个数是多少吗?
(3)小华画了一个如图⑤所示的斜框,小华能用这个斜框框出9个数的和为2016吗?若能,请求出第一行中间一个数,若不能,请说明理由.
题型10.行程问题
1.行程问题中有三个基本量:路程、时间、速度。
关系式为:①路程=速度×时间;②速度=;③时间=。
2.顺逆风(水)速度之间的关系:
①顺水(风)速度=静水(无风)速度+水流速度(风速);
②逆水(风)速度=静水(无风)速度-水流速度(风速)。
3. 追击问题的一个最基本的公式:追击时间速度差追击的路程.
相遇问题的基本公式为:速度和相遇时间路程.
4.环形跑道问题
环形跑道问题特殊场地行程问题之一。是多人(一般至少两人)多次相遇或追及的过程解决多人多次相遇与追击问题的关键是看我们是否能够准确的对题目中所描述的每一个行程状态作出正确合理的线段图进行分析。
在做出线段图后,反复的在每一段路程上利用:路程和=相遇时间×速度和
路程差=追及时间×速度差
解环形跑道问题的一般方法:
环形跑道问题,从同一地点出发,如果是相向而行,则每合走一圈相遇一次;如果是同向而行,则每追上一圈相遇一次.这个等量关系往往成为我们解决问题的关键。
18.快车以200km/h的速度由甲地开往乙地再返回甲地,慢车以75km/h的速度同时从乙地出发开往甲地.已知当快车回到甲地时,慢车距离甲地还有225km,则
(1)甲乙两地相距多少千米?
(2)从出发开始,经过多长时间两车相遇?
(3)几小时后两车相距100千米?
题型11.方案决策问题
19.当前在多措并举、全力推进青少年校园足球热烈氛围中,某体育用品商店对甲、乙两品牌足球开展促销活动,已知甲、乙两品牌足球的标价分别是:160元/个,60元/个,现有如下两种优惠方案:
方案一:不购买会员卡时,甲品牌足球享受8.5折优惠,乙品牌足球买5个(含5个)以上时所有球享受8.5折,5个以下必须按标价购买;
方案二:办理一张会员卡100元,会员卡只限本人使用,全部商品享受7.5折优惠.
(1)若购买甲品牌足球3个,乙品牌足球4个,哪一种方案更优惠?多优惠多少元?
(2)如果购买甲品牌足球若干个,乙品牌足球6个,方案一与方案二所付钱数一样多,求购买甲品牌的足球个数.
20.某电器商销售一种微波炉和电磁炉,微波炉每台定价800元,电磁炉每台定价200元.“双十一”期间商场决定开展促销活动,活动期间向客户提供两种优惠方案.
方案一:买一台微波炉送一台电磁炉;
方案二:微波炉和电磁炉都按定价的90%付款.
现某客户要到该卖场购买微波炉2台,电磁炉x台(x>2).
(1)若该客户按方案一购买,需付款 元.(用含x的代数式表示)
若该客户按方案二购买,需付款 元.(用含x的代数式表示)
(2)若x=5时,通过计算说明此时按哪种方案购买较为合算?
(3)当x=5时,你能给出一种更为省钱的购买方案吗?试写出你的购买方法.
21.元旦期间,某超市打出促销广告,如表所示,
小明妈妈第一次购物用了134元,第二次购物用了490元
(1)小明妈妈第一次所购物品的原价是 元
(2)小明妈妈第二次所购物品的原价是多少元?(列方程解决)
(3)若小明妈妈将两次购买的物品一次性购买,可比两次购买节省多少元?
题型12.古代问题中的一元一次方程
22.三个渔夫一起钓鱼,钓满了一桶鱼后他们都睡着了.渔夫甲先醒来后,把鱼数了一遍,拿出一条放入河里,然后拿起剩下的鱼的走了;过了一会,渔夫乙醒来,也把鱼数了一遍,拿出一条放入河里,又拿起剩下的鱼的走了;最后渔夫丙醒来一看,桶里还剩6条鱼.请你算一算,三个渔夫一共钓了多少条鱼?
23.阅读下列材料并回答问题:
墓碑上的数学题——他.我们熟悉的古希腊大数学家丢番图在数学上作出了伟大的贡献,被誉为数学界的鼻祖,用字母表示数和列方程解应用题等一些运算就是丢番图首创的,丟番图去世后,他的年龄成了一个谜,但它的墓碑上刻有一道数学题,让纪念他的人们根据墓碑上的题目,算出他的寿命.碑文是这样写的:这里是一座公慕,里面安葬着丢番图.他生命的是童年;再活了寿命的,颊上长出了细细的胡须;又过了一生的,他找到了终生伴侣;5年后,神赐给他一个儿子;可是儿子命运不济,只活了父亲岁数的一半,就匆匆离去;儿子死后,父亲在悲痛中生活了4年,也离开了人世.阅读后请用列方程解应用题的方法求丢番图寿命是多少岁?
一户居民一个月用电量的范围
电费价格(元/千瓦时)
不超过150千瓦时的部分
a
超过150千瓦时,但不超过300千瓦时的部分
b
超过300千瓦时的部分
a+0.3
参赛者
答对题数
答错题数
得分
A
28
2
108
B
26
4
96
C
24
6
84
队名
比赛场次
胜场
负场
积分
A
18
14
4
32
B
18
11
7
29
C
18
9
9
27
优惠条件
一次性购物不超过200元
一次性购物超过200元但不超过500元
一次性购物超过500元
优惠办法
无优惠
全部按9折优惠
其中500元仍按9折优惠,超过500元的部分按8折优惠
清单03 旋转(12个考点梳理+题型解读+核心素养提升+中考聚焦)-九年级上学期数学期末考点大串讲(人教版): 这是一份清单03 旋转(12个考点梳理+题型解读+核心素养提升+中考聚焦)-九年级上学期数学期末考点大串讲(人教版),文件包含清单03旋转12个考点梳理+题型解读+核心素养提升+中考聚焦原卷版docx、清单03旋转12个考点梳理+题型解读+核心素养提升+中考聚焦解析版docx等2份试卷配套教学资源,其中试卷共63页, 欢迎下载使用。
清单03 整式的乘除与因式分解 全章复习 (3个考点梳理+13种题型解读)(原卷版+解析版): 这是一份清单03 整式的乘除与因式分解 全章复习 (3个考点梳理+13种题型解读)(原卷版+解析版),文件包含清单03整式的乘除与因式分解全章复习3个考点梳理+13种题型解读原卷版docx、清单03整式的乘除与因式分解全章复习3个考点梳理+13种题型解读解析版docx等2份试卷配套教学资源,其中试卷共39页, 欢迎下载使用。
清单08 锐角三角函数(8个考点梳理+题型解读+核心素养提升+中考聚焦)-2023-2024学年九年级数学上学期期末考点预测(人教版): 这是一份清单08 锐角三角函数(8个考点梳理+题型解读+核心素养提升+中考聚焦)-2023-2024学年九年级数学上学期期末考点预测(人教版),文件包含清单08锐角三角函数8个考点梳理+题型解读+核心素养提升+中考聚焦原卷版docx、清单08锐角三角函数8个考点梳理+题型解读+核心素养提升+中考聚焦解析版docx等2份试卷配套教学资源,其中试卷共74页, 欢迎下载使用。












