江苏省扬州中学2023-2024学年高一上学期12月月考数学试题

这是一份江苏省扬州中学2023-2024学年高一上学期12月月考数学试题，共8页。试卷主要包含了单项选择题，多项选择题，填空题，解答题等内容，欢迎下载使用。

一、单项选择题：本题共8小题，每小题5分，共40分，在每小题给出的四个选项中，只有一项是符合题目要求.
1．已知集合，则（ ）
A． B． C． D．
2．命题有实数根，若是假命题，则实数的取值范围是（ ）
A．B．C．D．以上都不对
3．在平面直角坐标系中，角和的顶点与原点重合，始边与轴的正半轴重合，若角和的终边关于轴对称，则下列关系式一定正确的是（ ）
A．（）B．（）
C．（）D．（）
4．已知函数（a＞0且a≠1）的图象恒过定点A，若点A的坐标满足关于的方程，则的最小值为（ ）
A．9B．24C．4D．6
5．已知为锐角，且，则（ ）
A．B．C．D．
6．已知函数，当时，取得最小值，则m的取值范围为（ ）
A．B．C．D．
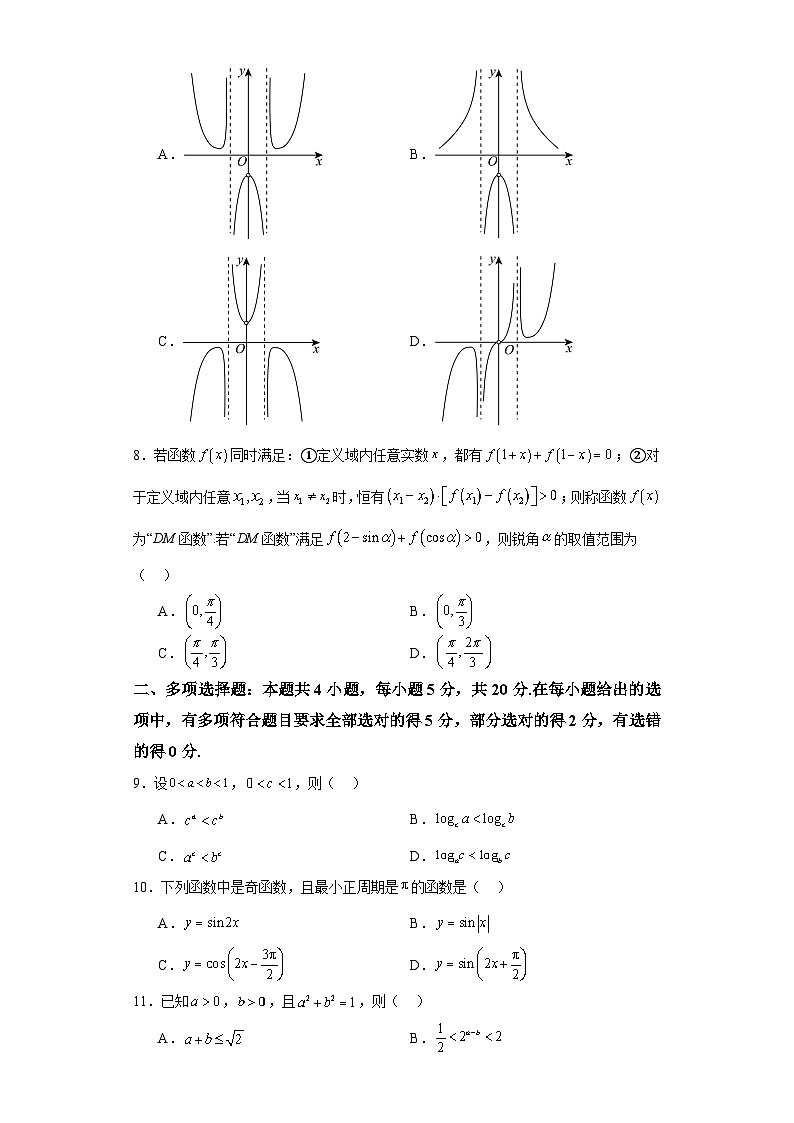
7．我国著名数学家华罗庚曾说：“数缺形时少直观，形缺数时难入微，数形结合百般好，隔裂分家万事休．”在数学的学习和研究中，常用函数的图像来研究函数的性质，也常用函数的解析式来分析函数的图像的特征，函数的图像大致是（ ）
A．B．
C．D．
8．若函数同时满足：①定义域内任意实数，都有；②对于定义域内任意，当时，恒有；则称函数为“DM函数”.若“DM函数”满足，则锐角的取值范围为（ ）
A．B．
C．D．
二、多项选择题：本题共4小题，每小题5分，共20分.在每小题给出的选项中，有多项符合题目要求全部选对的得5分，部分选对的得2分，有选错的得0分.
9．设，，则（ ）
A．B．
C．D．
10．下列函数中是奇函数，且最小正周期是的函数是（ ）
A．B．
C．D．
11．已知，，且，则（ ）
A．B．
C．D．
12．已知函数，则下列说法正确的是（ ）
A．若方程有4个不同的解，则实数k的取值范围为
B．关于x的方程有个不同的解
C．对于实数，不等式恒成立
D．当时，函数的图象与x轴围成的图形的面积为1
三、填空题：本大题共4小题，每小题5分，共20分.
13．已知幂函数在上单调递增，则的解析式是 .
14．函数的定义域为 .
15．数学中处处存在着美，莱洛三角形就给人以对称的美感．莱洛三角形的画法如下：先画等边三角形ABC，再分别以点A，B，C为圆心，线段AB长为半径画圆弧，便得到莱洛三角形（如图所示）．若莱洛三角形的周长为，则其面积是 .
16．设函数，方程有四个不相等的实根，则的取值范围是 .
四、解答题：本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.
17．已知 ， .
（1）若m=3，求；
（2）若，求实数m的取值范围.
18．化简或计算下列各式：
(1)；
(2).
19．已知.
(1)若，且，求的值；
(2)若，求的值.
20．已知某公司生产的一新款手机的年固定成本为万元，设该公司一年内共生产这种手机万部并全部销售完，且每万部的销售收入为万元，生产这种手机每年需另投入成本万元，且当.时，，当时，.
（1）写出年利润（万元）关于年产量（万部）的函数解析式（年利润年销售收入年成本）
（2）年产量为多少万部时，该公司所获年利润最大？最大年利润是多少？
21．已知定义域为R的函数是奇函数．
(1)判断的单调性，并证明；
(2)解关于的不等式．
22．对于函数.
(1)若方程恰有一个实根，求实数a的取值范围；
(2)设，若对任意，当时，满足，求实数a的取值范围．
参考答案：
一、单选题
1．D 2．B 3．D 4．C 5．D 6．B 7．A 8．A
二、多选题
9．CD 10．AC 11．ABD 12．AC
三、填空题
13． 14． 15． 16．
四、解答题
17．
（1）若m＝3，，
，
所以A∩B＝(2，5].
（2）因为，由题意得：，
，
因为A∪B＝B，有A⊆B，则有：，
解得：；
所以实数m的取值范围为.
18．
（1）原式＝
（2）原式＝
19．
（1）由已知，
由题意，
则；
（2）由，可知，
令，则，
20．
（1）当时，，
当时，，
.
（2）若，，
当时，；
若，，
当且仅当，即时，，
答：年产量为万部时，该公司所获年利润最大，最大年利润是万元.
21．
（1）因为是定义在R上的奇函数，则，
即
，解得，
所以，故在R上是递减函数．
证明：任取、，且，
，，
∴，即，故是定义在R上的递减函数；
（2）∵，∴，
是R上的奇函数，∴，
是R上的减函数，∴，
∴，解得，
∴不等式的解集为．
22．
（1）方程，
所以，
由①可得，，即，
当时，方程有唯一解，满足②，
所以符合条件；
当时，方程有两相等解，满足②，
所以符合条件；
当且时，方程有两不等解，
若满足②，则，
若满足②，则，
所以当时方程恰有一个实根；
综上，实数的取值范围为；
（2）令，则在上为减函数，在上为增函数，
∴函数在上为减函数，
当时，满足，
则，
∴，即对任意的恒成立，
设，又，所以函数在单调递增，
所以，
∴.