




北师大版(2021)拓展模块一 下册10.2.1 样本线性相关关系优质课课件ppt
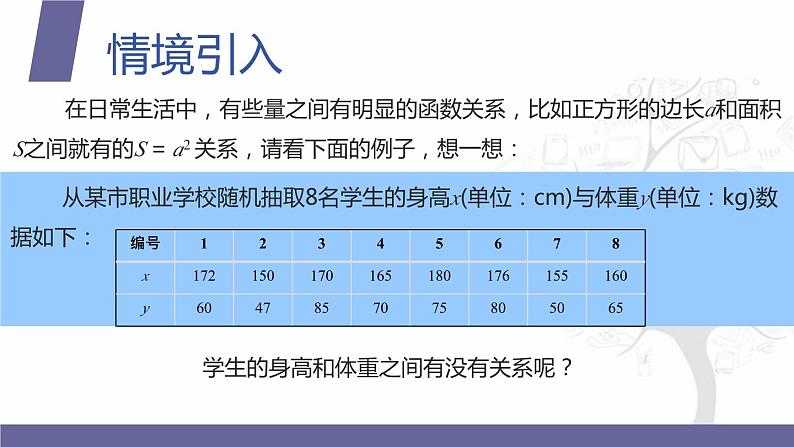
展开在日常生活中,有些量之间有明显的函数关系,比如正方形的边长a和面积S之间就有的S = a2 关系,请看下面的例子,想一想:
从某市职业学校随机抽取8名学生的身高x(单位:cm)与体重y(单位:kg)数据如下:
学生的身高和体重之间有没有关系呢?
学生的身高和体重之间有一定关系,根据经验可知,身高越高,体重也就越重.
但是,实际上,饮食习惯、体育锻炼、睡眠等因素也会影响体重.
所以,身高并不能完全确定体重.
因此,身高和体重的关系并不像以前研究过的函数关系.
如果两个变量有关系,但又不是确定性的必然关系,这种关系称为相关关系. 相关关系是一种随机关系,当一个变量的值确定后,另一个变量的值虽然与它有密切关系,但是仍无法完全确定.
例1. 下列关系中,属于相关关系的是( )
(1)扇形的半径与面积;(2)学生的学习态度与学习成绩;(3)出租车车费与行驶路程;(4)降雪量与交通事故的发生率.
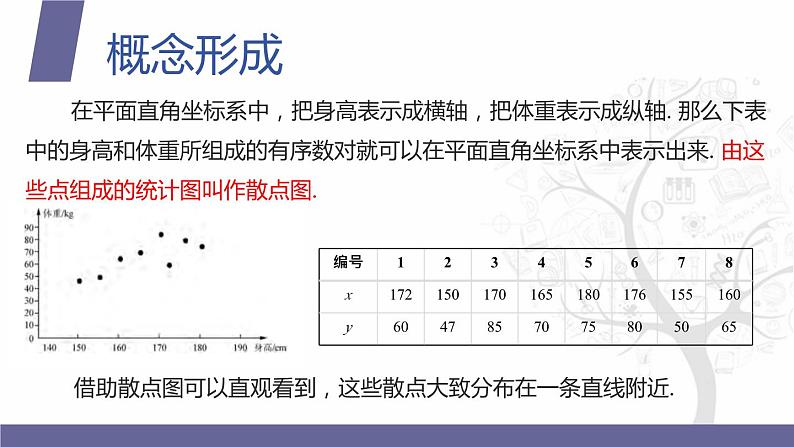
在平面直角坐标系中,把身高表示成横轴,把体重表示成纵轴. 那么下表中的身高和体重所组成的有序数对就可以在平面直角坐标系中表示出来. 由这些点组成的统计图叫作散点图.
借助散点图可以直观看到,这些散点大致分布在一条直线附近.
从整体上看,当一个变量的值增加时,另一个变量的相应值也呈现增加的趋势,我们就称这两个变量正相关; 如果当一个变量的值增加时,另一个变量的相应值呈现减少的趋势,则称这两个变量负相关.
一般地,如果两个变量的取值呈现正相关或负相关,且散点的分布大致落在一条直线的附近,就称这两个变量线性相关. 通常把研究两个变量之间的线性相关关系称为一元线性回归分析.
例2. 下面是水稻产量与施化肥量的一组观测数据(单位:kg/亩)
(1)将上述数据制成散点图;(2)你能从散点图中发现施化肥量与水稻产量近似成什么关系吗?
1.下列图中,两个变量x,y之间具有相关关系的是 .
2.下列散点图,两个变量x,y 之间具有相关关系的是 .
3.为了了解学生的计算能力,对某同学进行了10次试验,收集数据如下:
请画出散点图并判断它们是否具有线性相关关系.
线性相关:如果两个变量的取值呈现正相关或负相关,且散点的分布大致落在一条直线的附近,就称这两个变量线性相关.
相关关系:如果两个变量有关系,但又不是确定性的必然关系,这种关系称为相关关系.
北师大版(2021)拓展模块一 下册9.3正态分布授课ppt课件: 这是一份北师大版(2021)拓展模块一 下册9.3正态分布授课ppt课件,文件包含第22课正态分布pptx、北师大版《中职数学拓展模块一下册》第22课正态分布教学设计docx等2份课件配套教学资源,其中PPT共15页, 欢迎下载使用。
数学北师大版(2021)8.3.2 组合数公式优质ppt课件: 这是一份数学北师大版(2021)8.3.2 组合数公式优质ppt课件,文件包含北师大版《中职数学拓展模块一下册》第12课组合数公式课件pptx、北师大版《中职数学拓展模块一下册》第12课组合数公式教学设计docx等2份课件配套教学资源,其中PPT共14页, 欢迎下载使用。
中职数学北师大版(2021)拓展模块一 下册8.3.1 组合问题精品ppt课件: 这是一份中职数学北师大版(2021)拓展模块一 下册8.3.1 组合问题精品ppt课件,文件包含北师大版《中职数学拓展模块一下册》第11课组合问题课件pptx、北师大版《中职数学拓展模块一下册》第11课组合问题教学设计docx等2份课件配套教学资源,其中PPT共13页, 欢迎下载使用。












