初中数学人教版八年级下册19.1.1 变量与函数多媒体教学课件ppt

这是一份初中数学人教版八年级下册19.1.1 变量与函数多媒体教学课件ppt，文件包含第2课时函数pptx、心电图SimulatedPatientMonitormp4等2份课件配套教学资源，其中PPT共37页， 欢迎下载使用。

汽车耗油量为 0.1 L/km，油箱中有汽油 50 L. 如果在行驶过程中不再加油，那么下列各量中： ①汽车耗油量；②行驶路程x；③汽车油箱中的剩余油量y.变量是___________，常量是__________.
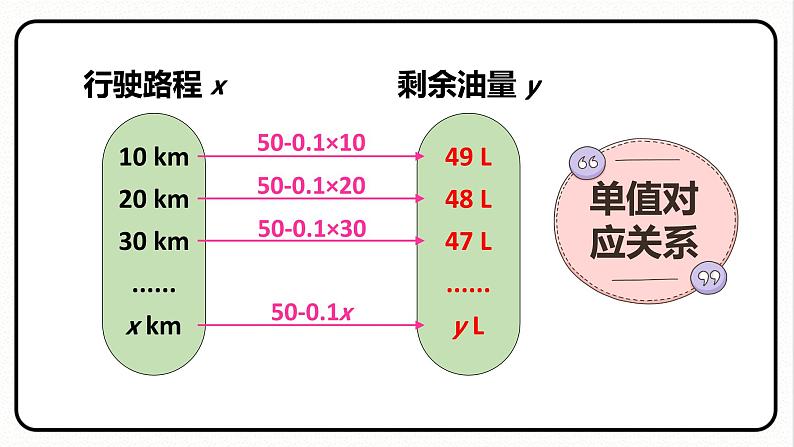
上面几个变量之间有什么联系吗？
对于用其他方式表示的变化过程，其中的两个变量是否也存在单值对应关系？大家能列举出对应的例子吗？
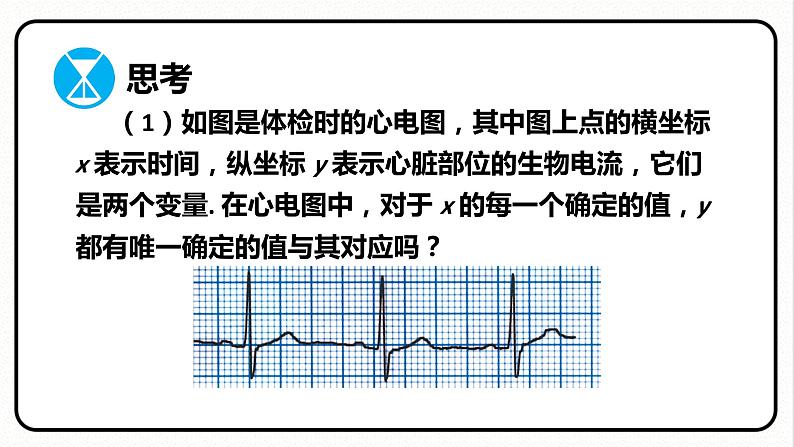
（1）如图是体检时的心电图，其中图上点的横坐标 x 表示时间，纵坐标 y 表示心脏部位的生物电流，它们是两个变量. 在心电图中，对于 x 的每一个确定的值，y 都有唯一确定的值与其对应吗？
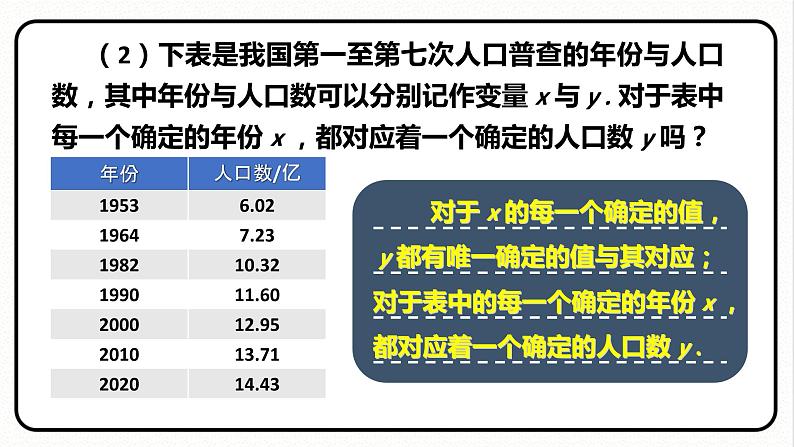
（2）下表是我国第一至第七次人口普查的年份与人口数，其中年份与人口数可以分别记作变量 x 与 y . 对于表中每一个确定的年份 x ，都对应着一个确定的人口数 y 吗？
对于 x 的每一个确定的值，y 都有唯一确定的值与其对应；
对于表中的每一个确定的年份 x ，都对应着一个确定的人口数 y .
一般地，在一个变化过程中，如果有两个变量 x 与 y，并且对于 x 的每一个确定的值，y 都有唯一确定的值与其对应，那么我们就说 x 是自变量，y 是 x 的函数.
P 是数轴上的一个动点，它所表示的实数是 m，P 点到坐标原点的距离为 s.（1）s 是 m 的函数吗？为什么？（2）m 是 s 的函数吗？为什么？
解：（1）s 是 m 的函数，因为对于 m 的每一个取值，s 都有唯一确定的值与其对应.
解：（2）m 不是 s 的函数，因为对于 s 除 0 外的每一个取值，m 有两个不同的值，不满足唯一对应性.
（2）m 是 s 的函数吗？为什么？
（1）s 是 m 的函数吗？为什么？
如果当 x = a 时 y = b，那么 b 叫做当自变量的值为 a 时的函数值.
函数是变量，函数值是某个具体的数值，即常数. 一个函数可能有许多不同的函数值. 如：在左面的表格中，年份 x 是自变量，人口数 y 是 x 的函数，是一个变量，表中的 12.52 是 y 的一个函数值.
已知函数 y = 2x－5 ，当 y = 5 时， x = ______.已知鞋子的“码数”y 与“厘米数”x 满足关系式 y = 2x－10，则 22 cm 的鞋子为______码.
是刻画变量之间对应关系的数学模型，许多问题中变量之间的关系都可以用函数来表示.
例 1 汽车油箱中有汽油 50 L. 如果不再加油，那么油箱中的油量 y（单位：L）随行驶路程 x（单位：km）的增加而减少，耗油量为 0.1 L/km. （1）写出表示 y 与 x 的函数关系的式子；（2）指出自变量 x 的取值范围；（3）汽车行驶 200 km时，油箱中还有多少汽油？
（1）写出表示 y 与 x 的函数关系的式子；
（1）行驶路程 x 是自变量，油箱中的油量 y 是 x 的函数.当行驶路程为 x 时，行驶中的耗油量为 0.1x.等量关系：油箱中的油量 = 原有油量－行驶中的耗油量 y = 50 － 0.1x
所以 y 与 x 的函数关系可表示为 y = 50 － 0.1x.
（2）指出自变量 x 的取值范围；
（2）仅从式子 y = 50 － 0.1x 看，x 可以取任意实数. 但是考虑到 x 代表的实际意义为行驶路程，因此 x 不能取负数. 行驶中的耗油量为 0.1x，它不能超过油箱中现有汽油量 50，即0.1x 50.因此，自变量 x 的取值范围是 0  x  500.
确定自变量的取值范围时，不仅要考虑使函数关系式有意义，而且还要注意问题的实际意义.
求自变量的取值范围，可转化为求不等式（组）的解集.
使根号下的式子为大于或等于0的实数
使各部分都有意义的实数的公共部分
（3）汽车行驶 200 km时，油箱中还有多少汽油？
（3）汽车行驶 200 km时，油箱中的汽油量是函数 y = 50 － 0.1x 在 x = 200 时的函数值. 将 x = 200 带入 y = 50 － 0.1x，得y = 50－0.1×200 = 20. 汽车行驶 200 km时，油箱中还有 30 L汽油.
像 y = 50 － 0.1x 这样，用关于自变量的数学式子表示函数与自变量之间的关系，是描述函数的常用方法. 这种式子叫做函数的解析式.
一名老师带领 x 名学生到某景点参观，若该景点的成人票每张 60 元，学生票每张 40 元，他们买门票的总费用为 y 元，则 y 关于 x 的函数解析式为____________.
y = 40x +60
下列两个变量之间不存在函数关系的是（ ）圆的面积 S 和半径 r 之间的关系一个正数 b 的平方根 a 与这个正数之间的关系某班学生的身高 y 与该班学生的学号 x 的关系某地一天的温度 T 与时间 t 的关系
2. 下列问题中哪些量是自变量？哪些量是自变量的函数？ 试写出函数的解析式.（1）改变正方形的边长 x ，正方形的面积 S 随之改变.
解：（1）自变量：正方形的边长 x； 自变量的函数：正方形的面积 S； 函数解析式： S = x2.
（2）每分向一水池注水 0.1 m3，注水量 y（单位：m3）随注水时间 x（单位：min）的变化而变化.（3）秀水村的耕地面积是 106 m2，这个村人均占有耕地面积 y（单位：m2）随这个村人数 n 的变化而变化.（4）水池中有水 10 L，此后每小时漏水 0.05 L，水池中的水量 V（单位：L）随时间 t（单位：h）的变化而变化.
（2）自变量：注水时间 x；自变量的函数：注水量 y；函数解析式： y = 0.1x.
（4）自变量：时间 t；自变量的函数：水池中的水量 V；函数解析式： V = 10－0.05t.
确定函数解析式的方法：
1. 找：找出变量和常量；2. 定：确定包含变量和常量的等量关系；3. 列：根据等量关系列出等式；4. 变：将等式变形，写成用含自变量的式子表示 函数的形式，得出函数解析式.
3. 按如图所示的程序计算函数 y 的值，若输入 x 的值为 -3，则输出 y 的值为_________.
5. 要用 20 m 长的绳子围成一个矩形，写出矩形的面积 S （单位：m2）关于矩形的一边长 x （单位：m）的函数解析式，并写出自变量 x 的取值范围.
要使实际问题有意义，则
所以 0 < x < 10.
故矩形的面积 S 关于矩形的一边长 x 的函数解析式为
S = - x2+10x（0 < x < 10）.
6. 如图，正方形 ABCD 的边长为 4 cm，E，F 分别是 BC，DC 边上的动点. 点 E，F 同时从点 C 处出发，均以 1 cm/s 的速度分别向点 B，D 运动，当点 E 与点 B 重合时，两点均停止运动. 设运动时间为 x s，运动过程中 △AEF的面积为 y cm2.
（1）写出 y 关于 x 的函数解析式，并写出自变量 x 的取值范围.
S△AEF = S正方形ABCD - S△ABE - S△ADF - S△ECF
不规则图形的面积转化为规则图形面积的差
解：由题意，得 CE = CF = x cm，所以 BE = DF =（4 - x）cm.
即 y 关于 x 的函数解析式为
速度、时间转化为线段的长度
（2）当点 E 运动到 BC 的中点时，求△AEF 的面积.
解：当点 E 运动到 BC 的中点时， x = CE = 2 cm，
所以当点 E 运动到 BC 的中点时，△AEF 的面积是 6 cm2.