浙江省舟山市2023年八年级上学期期末数学试题 附答案

这是一份浙江省舟山市2023年八年级上学期期末数学试题 附答案，共15页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

一、单选题
1．下列四个数学符号中，是轴对称图形的是（ ）
A．B．C．D．
2．如图，△ABC中AC边上的高是哪条垂线段.（ ）
A．AEB．CDC．BFD．AF
3．在△ABC中，已知AB=3，BC=4，则AC的长可能是（ ）
A．1B．4C．7D．9
4．下列选项中a的值，可以作为命题“则”是假命题的反例是（ ）
A．B．C．D．
5．将点A向左平移3个单位，再向上平移4个单位得到点B，则点B的坐标是（ ）
A．（-5，-7）B．（-5，1）C．（1，1）D．（1，-7）
6．在某一阶段，某商品的销售量与销售价之间存在如下关系：
设该商品的销售价为x元，销售量为y件，估计当x=127时，y的值为（ ）
A．63B．59C．53D．43
7．关于一次函数y=3x-1的描述，下列说法正确的是（ ）
A．图象经过第一、二、三象限
B．函数的图象与x轴的交点是（0，-1）
C．向下平移1个单位，可得到y=3x
D．图象经过点（1，2）
8．如图，在Rt∆ ABC中，∠B＝90°，作AC的中垂线l交BC于点D，连接AD，若AB＝3，BC＝9，则BD的长为（ ）
A．6B．5C．4D．3
9．对于任意实数p、q，定义一种运算：p@q＝p-q＋pq，例如2@3＝2-3＋2×3.请根据上述定义解决问题：若关于x的不等式组有3个整数解，则m的取值范围为是 （ ）
A．-8≤m<-5B．-810．如图，在等腰中，，，于点D，点P是延长线上一点，点O在延长线上，，下面的结论：①；②是正三角形；③；④，其中正确的个数是（ ）
A．1个B．2个C．3个D．4个
二、填空题
11．“x的5倍与y的差大于1”用不等式表示为 .
12．点P（2，3）关于x轴的对称点的坐标为 ．
13．命题“等腰三角形的两个底角相等”的逆命题是 ，它是 命题（填“真”或“假”）
14．如图，直线mn，以直线m上的点A为圆心，适当长为半径画弧，分别交直线m，n于点B、C，连接AC、BC，若∠1＝30°，则∠2＝ .
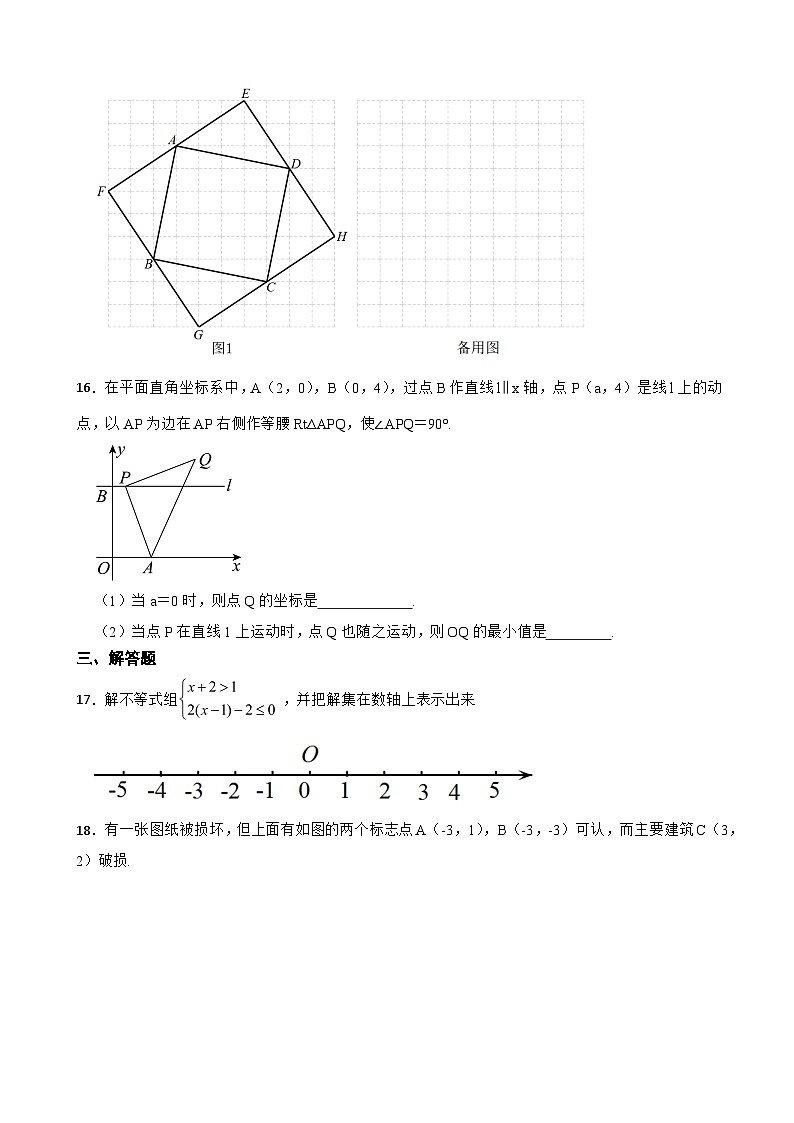
15．在边长为1的网格图形中，以顶点都是格点的正方形ABCD的边为斜边，向外作四个全等的直角三角形，使四个直角顶点E，F，G，H都是格点，且四边形EFGH为正方形，在图1所示的格点图形中，正方形ABCD的边长为，此时正方形EFGH的面积为52.写出正方形EFGH的面积的所有可能值是 （不包括52）.
16．在平面直角坐标系中，A（2，0），B（0，4），过点B作直线lx轴，点P（a，4）是线l上的动点，以AP为边在AP右侧作等腰Rt∆APQ，使∠APQ＝90°.
（1）当a＝0时，则点Q的坐标是 .
（2）当点P在直线1上运动时，点Q也随之运动，则OQ的最小值是 .
三、解答题
17．解不等式组，并把解集在数轴上表示出来.
18．有一张图纸被损坏，但上面有如图的两个标志点A（-3，1），B（-3，-3）可认，而主要建筑C（3，2）破损.
（1）建立直角坐标系；
（2）标出图中C点的位置；
（3）求出线段AC的长.
19．如图，已知在四边形ABCD中，ADBC，∠A＝90°，AD＝BE，CE⊥BD，垂足为E.
（1）求证：BD＝BC；
（2）若∠DBC＝50°，求∠DCE的度数.
20．如图，直线y=kx+b经过点A（-5，0），B（-1，4）
（1）求直线AB的表达式；
（2）求直线CE：y=-2x-4与直线AB及y轴围成图形的面积；
（3）根据图象，直接写出关于x的不等式kx+b＞-2x-4的解集.
21．为响应舟山市创建全国文明城市，某校决定安装垃圾分类的温馨提示牌和垃圾箱，若购买2个温馨提示牌和3个垃圾箱共需550元，且垃圾箱的单价是温馨提示牌单价的3倍.
（1）购买1个温馨提示牌和1个垃圾箱各需多少元？
（2）如果需要购买温馨提示牌和垃圾箱共100个，费用不超过8000元，问：最多购买垃圾箱多少个？
22．小玲和小东姐弟俩分别从家和图书馆同时出发，沿同一条路相向而行，小玲开始跑步中途改为步行，到达图书馆恰好用30分钟.小东骑自行车以300米/分钟的速度直接回家，两人离家的路程y（米）与各自离开出发地的时间x（分钟）之间的函数图象，如图所示：
（1）家与图书馆之间的路程为多少米？小玲步行的速度为多少？
（2）求小东离家的路程y关于x的函数解析式，并写出自变量的取值范围；
（3）当两人相遇时，他们离图书馆多远？
23．如果有两点到一条直线的距离相等，那么称这条直线为“两点的等距线”.
（1）如图1，直线CD经过线段AB的中点P，试说明直线CD是点A、B的一条等距线.
（2）如图2，A、B、C是正方形网格中的三个格点，请在网格中作出所有的直线m，使直线m过点C且直线m是“A、B的等距线”.
（3）如图3，∆ABC中，A（1，-2），B（4，-1），C（2，-0.5）.坐标轴上是否存在点P，使S∆APC＝S∆BPC，若存在，求出点P的坐标；若不存在，请说明理由.
24．（1）如图1，在Rt∆ABC中，AB＝AC，D是直线BC上的一点，将线段AD绕点A逆时针旋转90°至AE，连接CE，求证：∆ABD≌∆ACE；
（1）如图2，A是∆BDC内一点，∠ABC＝∠ADB＝45°，∠BAC＝90°，BD＝6，线段AD绕点A逆时针旋转90°至AE，点D、E、B恰好共线，求∆BDC的面积；
（2）如图3，在图1的条件下，延长DE，AC交于点G，BF⊥AB交DE于点F，求证：FG＝AE.
1．B
2．C
3．B
4．B
5．B
6．C
7．D
8．C
9．B
10．C
11．5x﹣y＞1
12．（2，﹣3）
13．两个角相等三角形是等腰三角形；真
14．75°
15．36或50
16．（1）（4，6）
（2）
17．解：，
解不等式①，得x＞﹣1，
解不等式②，得x≤2，
所以原不等式组的解集为﹣1＜x≤2.
在数轴上表示为：
.
18．（1）解：建立直角坐标系如下图所示，
（2）解：图中C点的位置如下图所示，
（3）解：如下图，
∵在Rt△ACF中，∠AFC=90°，CF=1，FA=6，
∴，
19．（1）证明：∵AD∥BC，
∴∠ADB＝∠CBE，
∵∠A＝90°，CE⊥BD，
∴∠BEC＝∠A＝90°，
在△ABD和△ECB中，
，
∴△ABD≌△ECB（ASA），
∴BD＝CB；
（2）解：∵BD＝CB，
∴△BCD是等腰三角形，
∴∠BCD＝∠BDC＝（180°﹣∠DBC）＝（180°﹣50°）＝65°，
∵∠BEC＝∠BDC＋∠DCE＝90°，
∴∠DCE＝90°－∠BDC ＝90°﹣65°＝25°.
20．（1）解：∵直线y=kx+b经过点A（-5，0），B（-1，4），
，解得 ，
∴直线AB的表达式为：y=x+5；
（2）解：∵若直线y= -2x-4与直线AB相交于点C，
∴ ，解得 ，故点C（-3，2）.
∵y= -2x-4与y=x+5分别交y轴于点E和点D，∴D（0，5），E（0，-4），
直线CE：y= -2x-4与直线AB及y轴围成图形的面积为： DE•|Cx|= ×9×3= ；
（3）解：根据图象可得x＞-3.
21．（1）解：设购买1个温馨提示牌需要x元，购买1个垃圾箱需要y元，依题意得，
，
解得：，
所以购买1个温馨提示牌需要50元，购买1个垃圾箱需要150元；
（2）解：设购买垃圾箱m个，则购买温馨提示牌（100﹣m）个，依题意得：
50（100﹣m）+150m≤8000，
解得：m≤30，
答：最多购买垃圾箱30个.
22．（1）解：由图象可得，家与图书馆之间的路程为4000米，
小玲步行的速度为：（4000﹣2000）÷（30﹣10）
＝2000÷20
＝100（米/分钟），
答：家与图书馆之间的路程为4000米，小玲步行的速度为100米/分钟；
（2）解：点D的横坐标为：4000÷300＝，
∴点D的坐标为（，0），
设小东离家的路程y关于x的函数解析式为y＝kx+b，
∵点C（0，4000），D（，0）在该函数图象上，
∴，
解得，
即小东离家的路程y关于x的函数解析式为y＝﹣300x+4000，自变量的取值范围是0≤x≤）；
（3）解：小玲跑步的速度为：2000÷10＝200（米/分钟），
当两人相遇时，设他们走的时间为m分钟，
300m+200m＝4000，
解得m＝8，
即出发8分钟后两人相遇，
∴当两人相遇时，他们离图书馆距离为：300×8＝2400（米），
答：当两人相遇时，他们离图书馆2400米.
23．（1）证明：分别作AE⊥CD，BF⊥CD，垂足为E，F，如图1，
∴∠AEP＝∠BFP＝90°，
∵P是AB中点，
∴AP＝BP，
在△AEP和△AFP，
，
∴△AEP≌△BFP（AAS），
∴AE＝BF，
即直线CD是点A、B的一条等距线.
（2）解：如图2，直线m1、m2就是所作的直线；
（3）解：设直线AB的解析式为y＝kx+b，
∵A（1，﹣2），B（4，﹣1），
∴，
解得，
∴直线AB的解析式为y＝x﹣，
∵S△APC＝S△BPC，
∴A、B两点到直线PC的距离相等，
①如图3，当PC∥AB时，
设直线PC的表达式是，
∵PC∥AB，
∴，
把点C（2，-0.5）代入得﹣0.5＝，
解得，
∴此时直线PC的解析式为y＝x，
当x＝0时，y＝，
当 y＝0时，0＝x，解得x＝，
∴直线PC与坐标轴的交点为P（，0），Q（0，），
此时P，Q都满足条件.
②当直线CP过AB中点E时，如图4，
∵A（1，-2），B（4，-1），
∴由中点坐标公式可得AB中点E（，﹣），
设直线CP的表达式为，把点C（2，-0.5），E（，﹣）代入得，
，
解得，
∴直线CP的解析式为y＝﹣2x+，
当x＝0时，y＝，
当y＝0时，x＝，
∴点R的坐标是（0，），点S的坐标是（，0），
此时R，S都满足条件.
综上所述，点P的坐标为（，0）或（0，）或（0，）或（，0）.
24．（1）解：如图2，过点A作AE⊥AD交BD于E，则∠DAE＝90°，连接CE，
∵∠ADB＝45°，
∴△ADE是等腰直角三角形，
∴AD＝AE，∠AED＝45°，
则线段AD绕点A逆时针旋转90°至AE，点D、E、B恰好共线，连接CE，
∵∠ABC＝45°，∠BAC＝90°，
∴△ABC是等腰直角三角形，
∴AB＝AC，
∴∠DAE＋∠BAE＝∠BAC＋∠BAE，
∴∠DAB＝∠EAC，
在△ABD和△ACE中，
，
∴△ABD≌△ACE（SAS）.
∴CE＝BD＝6，
∴∠AEC＝∠ADB＝45°，
∴∠CED＝∠CEB＝∠AEC＋∠AED＝∠90°，
∴S△BDC＝•BD•CE＝×6×6＝18.
（2）证明：如图3，过点D作DK⊥DC交FB的延长线于K.
∵DK⊥CD，BF⊥AB，
∴∠BDK＝∠ABK＝90°，
∵AB＝AC，∠BAC＝90°，
∴∠ABC＝∠ACB＝45°，
∴∠DBK＝180°－∠ABK－∠ABC＝45°，
∴∠DBK＝∠K＝45°，
∴DK＝DB，
∵△ABD≌△ACE，
∴∠ABD＝∠ACE＝180°－∠ABC＝135°，DB＝EC＝DK，
∴∠ECG＝180°－∠ACE＝∠45°，
∵BF⊥AB，CA⊥AB，
∴AG∥BF，
∴∠G＝∠DFK，
在△ECG和△DKF中，
，
∴△ECG≌△DKF（AAS），
∴DF＝EG，
∵将线段AD绕点A逆时针旋转90°至AE，
∴∠DAE＝90°，AD＝AE，
∴△ADE是等腰直角三角形，
∴DE＝AE，
∴DF+EF＝AE，
∴EG+EF＝AE，
即FG＝AE.销售价/元
90
100
110
120
130
140
销售量/件
90
80
70
60
50
40