初中7.3 一元一次方程的解法课文内容课件ppt

这是一份初中7.3 一元一次方程的解法课文内容课件ppt，共16页。PPT课件主要包含了移项法则，合作探究，移项要点，另一边，故选C，利用移项解方程的步骤，合并同类项，系数化为1，巩固练习等内容，欢迎下载使用。

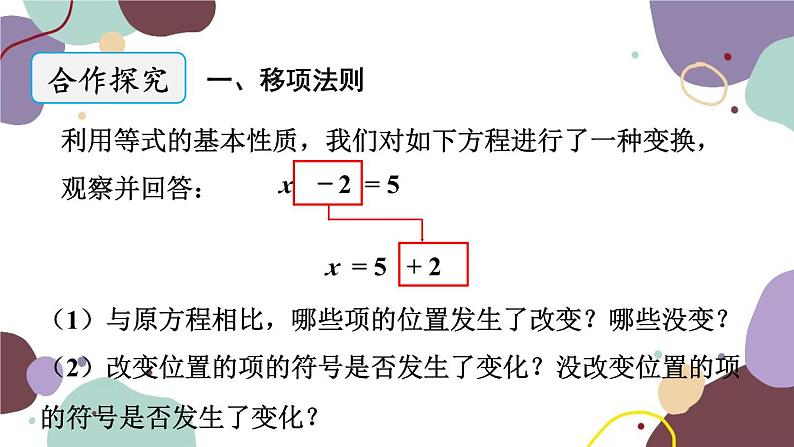
利用等式的基本性质，我们对如下方程进行了一种变换，观察并回答：
（1）与原方程相比，哪些项的位置发生了改变？哪些没变？（2）改变位置的项的符号是否发生了变化？没改变位置的项的符号是否发生了变化？
把原方程中的某一项改变________后，从________的一边移到________，这种变形叫做移项.
（1）移项的根据是等式的基本性质1.（2）移项要变号，没有移动的项不改变符号.（3）通常把含有未知数的项移到方程的左边，把常数项（不含未知数的项）移到方程的右边.
【例】 通过移项将下列方程变形，正确的是（ 　）A.由5x－7＝2，得5x＝2－7B.由6x－3＝x＋4，得3－6x＝4＋xC.由8－x＝x－5，得－x－x＝－5－8D.由x＋9＝3x－1，得3x－x＝－1＋9
A中由5x－7＝2，得5x＝2＋7，故选项A错误；
B中由6x－3＝x＋4，得3－6x＝－x－4，故选项B错误；
C中由8－x＝x－5，得－x－x＝－5－8，故选项C正确；
D中由x＋9＝3x－1，得3x－x＝9＋1，故选项D错误.
1.移项时必须是从等号的一边到另一边，并且不要忘记对移动的项变号，如从3＋5x＝12得到5x＝12＋3是不对的．2.没移项时不要误认为移项，如从-9＝x得到x＝-9，利用的是等式的基本性质（对称性）.两者要区分清楚．
二、利用移项、合并同类项解方程
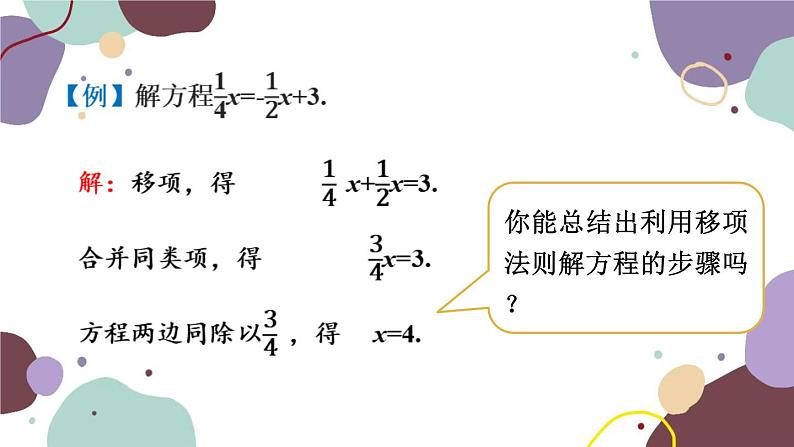
【例】解下列方程：（1）2x+6=1 （2）3x+3=2x+7
（2）移项，得 3x-2x=7-3.合并同类项，得 x=4.
你能总结出利用移项法则解方程的步骤吗？
解下列方程：（1）－x－4＝3x；　 （2）5x－1＝9；
解：（1）移项，得 -x-3x＝4，合并同类项，得 -4x＝4，系数化成1，得 x＝-1；
（2）移项，得 5x＝9＋1，合并同类项，得 5x＝10，系数化成1，得 x＝2；
（3）－4x－8＝4； （4）0.5x－0.7＝6.5－1.3x.
解：（3）移项，得 －4x＝4＋8，合并同类项，得 －4x＝12，系数化成1，得 x＝－3；
（4）移项，得 0.5x＋1.3x＝ 6.5＋0.7，合并同类项，得 1.8x＝7.2，系数化成1，得 x＝4.
利用解方程求未知数的值
1.对于方程-3x-7=12x+6，下列移项正确的是（ ） A. -3x-12x=6+7 B.-3x+12x= -7+6 C. -3x-12x=7-6 D.12x-3x=6+7
2.解下列方程：（1）-2x+5=-3； （2）10x-2=6x+1+3x.
解：（1）移项，得 -2x=-3-5，合并同类项，得 -2x=-8，系数化成1，得 x=4；
（2）移项，得 10x-6x-3x=1+2，合并同类项，得 x=3.