福建省龙岩市武平县2022-2023学年六年级下学期期中数学试卷

这是一份福建省龙岩市武平县2022-2023学年六年级下学期期中数学试卷，共5页。试卷主要包含了细心谨慎，仔细计算，用心思考，准确填空，实践应用.，操作题等内容，欢迎下载使用。

1．直接写出得数。
2．解方程或比例。
＝
0.5：x＝
：＝：x
4.8×2.5﹣75%x＝3
3．脱式计算，能简算的要简算。
（+）×+0.7＝
×+÷＝
3.5×0.8+5.5×80%+＝
二、用心思考，准确填空。
4． ÷30＝＝3： ＝60%＝： ＝ 折
5．200cm3＝ dm3
2.05L＝ L ML
45分＝ 时
6050kg＝ t
5dm2＝ cm2＝ m2
6．某食品包装袋上标注净含量为500±30克，这袋食品最少为 克，最多为 克。
7．2022年3月28日，某市新增新冠肺炎确诊病例16例，记作+16，治俞9例，记作 例。
8．为了观看“空中课堂”钉钉直播课，爸爸用八五折的价格为明明买了一台电脑，便宜了990元，购买这台电脑花了 元。
9．在一个比例中，两个内项互为倒数，其中一个外项是0.8，另一个外项是 。
10．李丹家去年收百香果800kg，今年收百果香960kg，今年百香果产量比去年增加了 成。
11．一张图纸上量的某零件长6cm，这个零件实际长2mm，这幅图纸的比例尺是 。
12．一个圆锥形沙堆，底面周长是18.84dm，高3dm，这个沙堆的体积是 。
13．2022年春节佳佳把2500元压岁钱存入银行，整存整取两年，年利率3.75%，到期时佳佳可以从银行中取出 元。
14．若a＝b，则a与b成 成比例关系，a：b＝ ： 。
15．把一个棱长为6dm的正方形木块，削成一个最大的圆柱，圆柱的体积是 dm3，把这个圆柱削成一个最大的圆锥，削去部分的体积是 dm3。
16．把一根长1.8m的圆柱形木材沿横截面截成两个圆柱体木材，截完后表面积比原来增加20cm²，这根木材原来的体积是 dm3。
17．如图，5个完全相同的小长方形刚好拼成一个大长方形。小长方形中，长与宽的比是 ，大长方形中，长与宽的比是 。
18．用棱长是1cm的正方体，拼成一个长4cm、宽3cm、高2cm的长方体．需要 块小正方体．
19．如图所示是正方体的展开图，如果a在上面，c在前面，那么左面是 ，右面是 ，后面是 。
20．一个正方体的底面积是25cm2，它的体积是 cm3。
21．一个无盖的长方体鱼缸，相交于一点的三条棱的长度分别是9cm、6cm、5cm，做这个鱼缸至少需要 cm2的玻璃。
22．把下面的假分数化成带分数或整数。
23．用2个完全相同的正方体木块，拼成一个长方体，已知长方体的棱长总和是96cm，则每个正方体的体积是 cm3。
24．当x＝ 时，＝2，当x＝ 时，＝1．
25．的分数单位是 ，把它化成带分数是 ，再加上 个这样的分数单位它就是最小的质数。
三、实践应用.
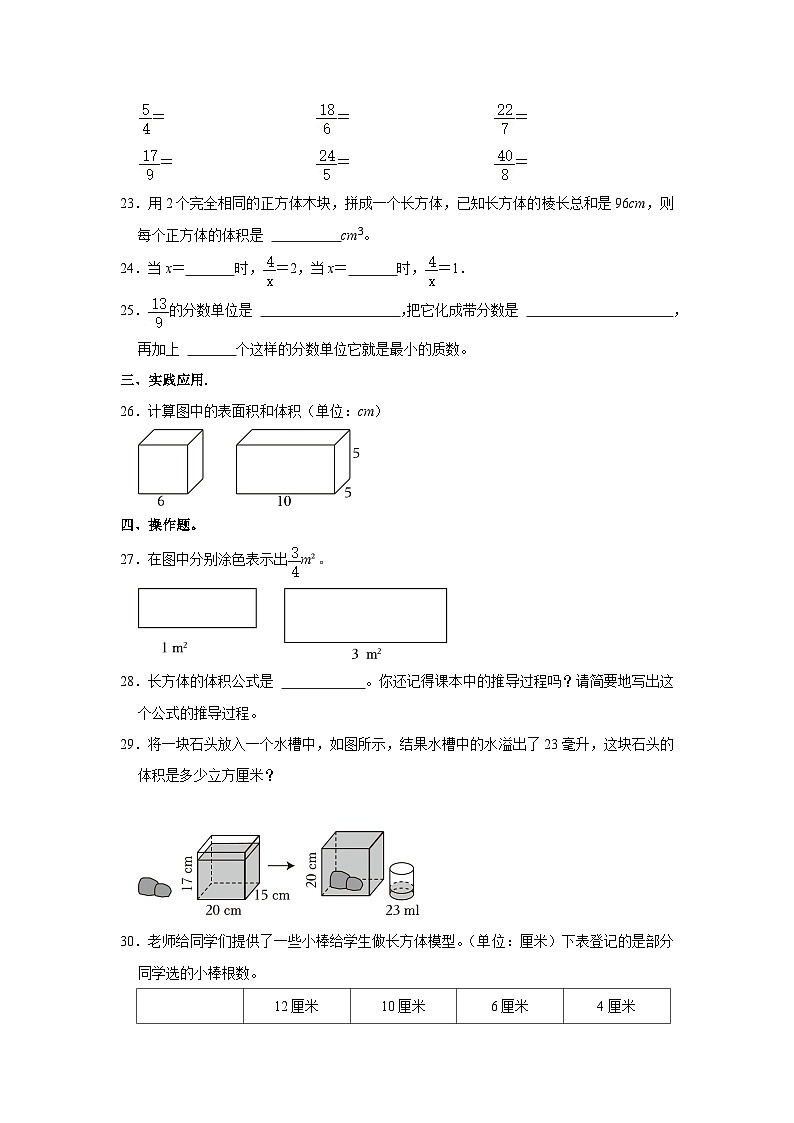
26．计算图中的表面积和体积（单位：cm）
四、操作题。
27．在图中分别涂色表示出m²。
28．长方体的体积公式是 。你还记得课本中的推导过程吗？请简要地写出这个公式的推导过程。
29．将一块石头放入一个水槽中，如图所示，结果水槽中的水溢出了23毫升，这块石头的体积是多少立方厘米？
30．老师给同学们提供了一些小棒给学生做长方体模型。（单位：厘米）下表登记的是部分同学选的小棒根数。
（1）这些同学选的小棒都能搭成长方体或正方体吗？说说谁的不能，为什么？
（2）我认为 选的小棒都能搭成长方体或正方体。长、宽、高或棱长各是多少？
（3）请你选择合适的小棒数，计算你所搭长方体的体积是多少？
31．某邮政运货车的车厢是长方体，从里面量长8m，宽2.6m，高2m，它的容积是多少立方米？
32．某海岛战士为解决岛上淡水缺水问题，和当地居民共同修建了一个长22米，宽10米，深1.8米的淡水蓄水池。
（1）这个蓄水池占地有多大？
（2）修建这个蓄水池要挖多少方的泥土？
（3）在四周和底部抹上水泥，抹水泥面积的有多大？
2022-2023学年福建省龙岩市武平县六年级（下）期中数学试卷
参考答案与试题解析
一、细心谨慎，仔细计算。
1．直接写出得数。
【分析】根据分数、小数、百分数乘除法以及四则混合运算的顺序，直接进行口算即可。
【解答】解：
【点评】本题考查了基本的运算，注意运算数据和运算符号，细心计算即可。
2．解方程或比例。
＝
0.5：x＝
：＝：x
4.8×2.5﹣75%x＝3
【分析】（1）根据比例的基本性质，先把比例化为方程，两边再同时除以72；
（2）根据比例的基本性质，先把比例化为方程，两边再同时除以0.6；
（3）根据比例的基本性质，先把比例化为方程，两边再同时乘2；
（4）先把原方程化为12﹣0.75x＝3，两边再同时加上0.75x，然后两边再同时减去3，最后两边再同时除以0.75。
【解答】解：（1）＝
72x＝7.2
72x÷72＝7.2÷72
x＝0.1
（2）0.5：x＝
0.6x＝1.2
0.6x÷0.6＝1.2÷0.6
x＝2
（3）：＝：x
x＝
2×x＝×2
x＝
（4）4.8×2.5﹣75%x＝3
12﹣0.75x＝3
12﹣0.75x+0.75x＝3+0.75x
3+0.75x﹣3＝12﹣3
0.75x＝9
0.75x÷0.75x＝9÷0.75
x＝12
【点评】熟练掌握比例的基本性质和等式的基本性质是解题的关键。
3．脱式计算，能简算的要简算。
（+）×+0.7＝
×+÷＝
3.5×0.8+5.5×80%+＝
【分析】（1）先算小括号里面的加法，再算乘法，最后算括号外面的加法；
（2）变除法为乘法，再按照乘法分配律计算；
（3）按照乘法分配律计算。
【解答】解：（1）（+）×+0.7
＝×+0.7
＝0.35+0.7
＝1.05
（2）×+÷
＝×+×
＝×（+）
＝×2
＝
（3）3.5×0.8+5.5×80%+
＝0.8×（3.5+5.5+1）
＝0.8×10
＝8
【点评】本题考查了四则混合运算，注意运算顺序和运算法则，灵活运用所学的运算定律进行简便计算。
二、用心思考，准确填空。
4． 18 ÷30＝＝3： 5 ＝60%＝： ＝ 六 折
【分析】根据已知的分数，利用分数的基本性质把分数的分子和分母同时乘一个不为0的数，得到与它相等的分数，再利用分子除以分母求出小数和除法算式及比即可。
【解答】解：18÷30＝＝3：5＝60%＝：＝六折
故答案为：18，5，，六。
【点评】此题考查小数、分数、百分数之间的转化，根据它们之间的关系和性质进行转化即可。
5．200cm3＝ 0.2 dm3
2.05L＝ 2 L 50 ML
45分＝ 0.75 时
6050kg＝ 6.05 t
5dm2＝ 500 cm2＝ 0.05 m2
【分析】根据1立方分米＝1000立方厘米，1升＝1000毫升，1小时＝60分，1吨＝1000千克，1平方米＝100平方分米，1平方分米＝100平方厘米，解答此题即可。
【解答】解：200cm3＝0.2dm3
2.05L＝2L50ML
45分＝0.75时
6050kg＝6.05t
5dm2＝500cm2＝0.05m2
故答案为：0.2；2；50；0.75；6.05；500；0.05。
【点评】熟练掌握体积单位、容积单位、时间单位、质量单位、面积单位的换算，是解答此题的关键。
6．某食品包装袋上标注净含量为500±30克，这袋食品最少为 470 克，最多为 530 克。
【分析】净含量：500±30克，这表示这袋食品只要在500+30＝530克和500﹣30＝470克之间都算合格；由此解答即可。
【解答】解：500+30＝530（克）
500﹣30＝470（克）
答：这袋食品最少为470克，最多为530克。
故答案为：470，530。
【点评】此题主要是考查学生对生活中净含量的理解。
7．2022年3月28日，某市新增新冠肺炎确诊病例16例，记作+16，治俞9例，记作 ﹣9 例。
【分析】用正负数表示意义相反的两种量：确诊人数增加记作正，减少记作负。由此得解。
【解答】解：2022年3月28日，某市新增新冠肺炎确诊病例16例，记作+16，治俞9例，记作﹣9例。
故答案为：﹣9。
【点评】此题主要考查正负数的意义，正数与负数表示意义相反的两种量，看清规定哪一个为正，则和它意义相反的就为负。
8．为了观看“空中课堂”钉钉直播课，爸爸用八五折的价格为明明买了一台电脑，便宜了990元，购买这台电脑花了 5610 元。
【分析】八五折即为原价的85%，原价是单位“1”，便宜了原价的1﹣85%，用便宜的钱数除以对应的百分率，即可求出原价是多少钱，再乘85%，即可求出实际花的钱数。
【解答】解：八五折＝85%
990÷（1﹣85%）
＝990÷15%
＝6600（元）
6600×85%＝5610（元）
答：购买这台电脑花了5610元。
故答案为：5610。
【点评】本题考查百分数的计算及应用。理解题意，找出数量关系，列式计算即可。
9．在一个比例中，两个内项互为倒数，其中一个外项是0.8，另一个外项是 1.25 。
【分析】依据比例的基本性质，即两内项之积等于两外项之积即可作答。
【解答】解：因为两个内项互为倒数，则两内项之积为1
所以两外项之积也为1，一个外项是0.8
则另一个外项为：1÷0.8＝1.25
故答案为：1.25。
【点评】此题主要考查比例的基本性质及倒数的意义。
10．李丹家去年收百香果800kg，今年收百果香960kg，今年百香果产量比去年增加了 二 成。
【分析】用今年的产量减去去年的产量，求出今年比去年多的产量，再除以去年的产量，再写成成数的形式，即可解答。
【解答】解：（960﹣800）÷800
＝160÷800
＝0.2
0.2＝20%＝二成
答：今年百香果产量比去年增加了二成。
故答案为：二。
【点评】本题考查成数的计算及应用。理解题意，找出数量关系，列式计算即可。
11．一张图纸上量的某零件长6cm，这个零件实际长2mm，这幅图纸的比例尺是 30：1 。
【分析】根据比例尺＝图上距离÷实际距离，代入数据解答即可。
【解答】解：6cm：2mm
＝60mm：2mm
＝60：2
＝30：1
答：这幅图纸的比例尺是30：1。
故答案为：30：1。
【点评】解答此题的关键是掌握比例尺＝图上距离÷实际距离这个公式及其变形。
12．一个圆锥形沙堆，底面周长是18.84dm，高3dm，这个沙堆的体积是 28.26立方米 。
【分析】沙堆的形状是圆锥形的，由底面周长是18.84米先求得底面半径，再利用圆锥的体积计算公式V＝πr2h求得体积，问题得解。
【解答】解：×3.14×（18.84÷3.14÷2）2×3
＝×3.14×32×3
＝3.14×9
＝28.26（立方米）
答：它的体积是28.26立方米。
故答案为：28.26立方米。
【点评】此题主要考查圆锥的体积计算公式V＝πr2h，运用公式计算时不要漏乘。
13．2022年春节佳佳把2500元压岁钱存入银行，整存整取两年，年利率3.75%，到期时佳佳可以从银行中取出 2687.5 元。
【分析】根据本息和＝本金+本金×利率×存期，代入数据解答即可。
【解答】解：2500+2500×2×3.75%
＝2500+187.5
＝2687.5（元）
答：到期时佳佳可以从银行中取出2687.5元。
故答案为：2687.5。
【点评】本题考查了存款利息相关问题，公式：本息和＝本金+本金×利率×存期。
14．若a＝b，则a与b成 正 成比例关系，a：b＝ 2 ： 3 。
【分析】判定两种相关联的量是否成正、反比例，要看这两种量是对应的比值一定，还是对应的乘积一定，如果是比值一定就成正比例；如果是乘积一定就成反比例；根据比例的基本性质，把a＝b改写成比例的形式，使a和做比例的外项，b和做比例的内项即可。
【解答】解：若a＝b，则a与b成正成比例关系，a：b＝：＝2：3。
故答案为：正，2，3。
【点评】解答此题的关键是比例基本性质的逆运用，要注意：相乘的两个数要做外项就都做外项，要做内项就都做内项；也考查了判断两个相关联的量成什么比例。
15．把一个棱长为6dm的正方形木块，削成一个最大的圆柱，圆柱的体积是 169.56 dm3，把这个圆柱削成一个最大的圆锥，削去部分的体积是 113.04 dm3。
【分析】根据题意可知，把这个正方体木块削成一个最大的圆柱，这个圆柱的底面直径和高都等于正方体的棱长，如果把这个圆柱再削成一个最大的圆锥，这个圆锥的体积是圆柱体积的，那么削去部分的体积相当于圆柱体积的（1﹣），根据圆柱的体积公式：V＝πr2h，把数据代入公式解答。
【解答】解：3.14×（6÷2）2×6
＝3.14×9×6
＝169.56（立方厘米）
169.56×（1﹣）
＝169.56×
＝113.04（立方厘米）
答：这个圆柱的体积是169.56立方厘米，削去部分的体积是113.04立方厘米。
故答案为：169.56，113.04。
【点评】此题主要考查圆柱体积公式的灵活运用，以及等底等高的圆柱和圆锥体积之间的关系及应用。
16．把一根长1.8m的圆柱形木材沿横截面截成两个圆柱体木材，截完后表面积比原来增加20cm²，这根木材原来的体积是 1.8 dm3。
【分析】根据题意可知，把这根圆柱形木料横截成两段后，表面积比原来增加两个截面的面积，据此可以求出一个截面（圆柱的底面）的面积，然后根据圆柱的体积＝底面积×高，把数据代入公式解答。
【解答】解：20平方厘米＝0.2平方分米
1.8米＝18分米
0.2÷2×18
＝0.1×18
＝1.8（立方分米）
答：这根木材原来的体积是1.8立方分米。
故答案为：1.8。
【点评】此题主要考查圆柱的表面积公式、体积公式的灵活运用，关键是熟记公式，注意面积单位、长度单位相邻单位之间的进率的及换算。
17．如图，5个完全相同的小长方形刚好拼成一个大长方形。小长方形中，长与宽的比是 3：2 ，大长方形中，长与宽的比是 6：5 。
【分析】观察图形，小长方形的3条宽的和等于小长方形2条长的和，据此设每个小长方形的宽是1，则小长方形的长是：1×3÷2＝，据此即可求出它们的比。
【解答】解：设每个小长方形的宽是1，则小长方形的长是：1×3÷2＝，则大长方形的长是3，宽是1+＝，
所以小长方形的长与宽的比是：1＝3：2；
大长方形的长与宽的比是3：＝6：5。
答：小长方形的长与宽的比是3：2，大长方形的长与宽的比是6：5。
故答案为：3：2，6：5。
【点评】解答此题的关键是根据图形得出小长方形的长与宽的关系，从而利用赋值法表示出它们的长与宽，再求比即可。
18．用棱长是1cm的正方体，拼成一个长4cm、宽3cm、高2cm的长方体．需要 24 块小正方体．
【分析】根据小正方体拼组长方体的方法可知，长方体的长需要4块小正方体，宽需要3块小正方体，高需要2块小正方体，由此借助长方体的体积公式即可解答．
【解答】解：4×3×2＝24（块），
答：一共需要24块小正方体．
故答案为：24．
【点评】抓住小正方体拼组长方体的方法，得出每条棱长上需要的小正方体的个数，再利用长方体的体积公式即可解答．
19．如图所示是正方体的展开图，如果a在上面，c在前面，那么左面是 b ，右面是 d ，后面是 f 。
【分析】观察图形可知，该正方体展开图属于“1﹣3﹣2”型，a相对的面是e，b相对的面是d，c相对的面是f，c的左面是b，右面是d，据此解答即可。
【解答】解：如果a在上面，c在前面，那么左面是b，右面是d，后面是f。
故答案为：b；d；f。
【点评】本题考查正方体的展开图，明确正方体的特征是解题的关键。
20．一个正方体的底面积是25cm2，它的体积是 125 cm3。
【分析】首先根据正方形的面积公式：S＝a2，求出正方体的棱长，再根据正方体的体积公式：V＝a3，求出正方体的体积。
【解答】解：因为5的平方是25，所以正方体的棱长是5厘米。
5×5×5＝125（立方厘米）
答：它的体积是125立方厘米。
故答案为：125。
【点评】此题主要考查正方形的面积公式、正方体的体积公式的灵活运用，关键是熟记公式。
21．一个无盖的长方体鱼缸，相交于一点的三条棱的长度分别是9cm、6cm、5cm，做这个鱼缸至少需要 204 cm2的玻璃。
【分析】由题意可知，相交于一点的三条棱就是长方体的长、宽和高，求无盖鱼缸的面积就是求长方体五个面的面积，再根据长方体五个面的计算方法：S＝（ah+bh）×2+ab，据此计算即可。
【解答】解：（9×5+6×5）×2+9×6
＝（45+30）×2+54
＝75×2+54
＝150+54
＝204（cm2）
则做这个鱼缸至少需要204cm2的玻璃。
故答案为：204。
【点评】本题考查长方体的表面积，熟记公式是解题的关键。
22．把下面的假分数化成带分数或整数。
【分析】根据分数与除法的关系，用分子除以分母，得到的商是带分数的整数部分，余数作分子，分母不变，如果正好整除，可以直接把假分数化成整数。
【解答】解：
【点评】本题解题的关键是熟练掌握假分数化成带分数或整数。
23．用2个完全相同的正方体木块，拼成一个长方体，已知长方体的棱长总和是96cm，则每个正方体的体积是 216 cm3。
【分析】根据2个完全相同的正方体拼组长方体的方法可知，长方体的棱长之和是小正方体的16个棱长的和，由此即可求出小正方体的棱长是96÷16＝6cm，代入体积公式计算即可得解。
【解答】解：96÷16＝6（cm）
6×6×6
＝36×6
＝216（cm3）
答：每个正方体的体积是216cm3。
故答案为：216。
【点评】抓住2小正方体拼组长方体的特点，根据棱长总和先求出小正方体的棱长是解决此题的关键。
24．当x＝ 2 时，＝2，当x＝ 4 时，＝1．
【分析】（1）根据等式的性质两边同乘x，得2x＝4，再根据等式的性质，两边同除以2即可．
（2）根据等式的性质，两边同乘x，得x＝4．
【解答】解：（1）＝2
×x＝2×x
2x＝4
2x÷2＝4÷2
x＝2
（2）＝1
×x＝1×x
x＝4
答：当x＝2时，＝2，当x＝4时，＝1
故答案为：2，1．
【点评】此题考查了根据等式的性质解方程，即等式两边同加上、同减去、同乘上或同除以一个不为0的数，等式仍相等．同时注意“＝”上下要对齐．
25．的分数单位是 ，把它化成带分数是 1 ，再加上 5 个这样的分数单位它就是最小的质数。
【分析】根据分数单位的意义，把单位“1”平均分成若干份，表示其中1份的数叫分数单位，因此，这个分数的分数单位是；假分数化带分数时，用分子除以分母，商为整数部分，余数作分子，分母不变；最小的质数是2，2与的差是，所以需要再添上5个这个样的分数单位就是最小的质数。
【解答】解：的分数单位是，把它化成带分数是1，再加上5个这样的分数单位它就是最小的质数。
故答案为：，1，5。
【点评】本题主要考查的知识点有：分数及分数单位的意义、假分数化带分数、质数的意义等。
三、实践应用.
26．计算图中的表面积和体积（单位：cm）
【分析】根据长方体的表面积公式：S＝（ab+ah+bh）×2，体积公式：V＝abh，正方体的表面积公式：S＝6a2，体积公式：V＝a3，把数据代入公式解答。
【解答】解：（1）6×6×6
＝36×6
＝216（平方厘米）
6×6×6
＝36×6
＝216（立方厘米）
答：正方体的表面积是216平方厘米，体积是216立方厘米。
（2）（10×5+10×5+5×5）×2
＝（50+50+25）×2
＝125×2
＝250（平方厘米）
10×5×5
＝50×5
＝250（立方厘米）
答：长方体的表面积是250平方厘米，体积是250立方厘米。
【点评】此题主要考查长方体、正方体的表面积公式、体积公式的灵活运用，关键是熟记公式。
四、操作题。
27．在图中分别涂色表示出m²。
【分析】把1平方米看作单位“1”，把它平均分成4份，每份是它的，是平方米，平方米表示其中3份；把3平方米看作单位“1”，把它平均分成4份，每份是它的，是平方米。
【解答】解：
【点评】关键弄清平方米是1平方米的几分之几，3平方米的几分之几。
28．长方体的体积公式是 V＝abh 。你还记得课本中的推导过程吗？请简要地写出这个公式的推导过程。
【分析】长方体体积公式是：V＝abh （a表示长、b表示宽、h表示高）。根据长方体体积公式的推导过程：用体积是1立方厘米的正方体学具（教具），摆出不同的长方体，摆出的长方体的体积正好等于所摆长方体的长、宽、高的乘积。由此推导出长方体的体积公式。
【解答】解：长方体体积公式是：V＝abh （a表示长、b表示宽、h表示高）。
用体积是1立方厘米的正方体学具（教具），摆出不同的长方体，摆出的长方体的体积正好等于所摆长方体的长、宽、高的乘积。由此推导出长方体的体积公式。
故答案为：V＝abh。
【点评】此题考查的目的是理解掌握长方体体积公式的推导过程及应用。
29．将一块石头放入一个水槽中，如图所示，结果水槽中的水溢出了23毫升，这块石头的体积是多少立方厘米？
【分析】题意可知，这块石头的体积等于容器中上升的水的体积加上溢出的水的体积，再根据不规则物体的体积＝容器的底面积×水面上升的高度，据此解答即可。
【解答】解：23毫升＝23立方厘米
20×15×（20﹣17）+23
＝300×3+23
＝900+23
＝923（立方厘米）
答：这块石头的体积是923立方厘米。
【点评】本题考查求不规则物体的体积，明确石头的体积等于容器中上升的水的体积加上溢出的水的体积是解题的关键。
30．老师给同学们提供了一些小棒给学生做长方体模型。（单位：厘米）下表登记的是部分同学选的小棒根数。
（1）这些同学选的小棒都能搭成长方体或正方体吗？说说谁的不能，为什么？
（2）我认为 聪聪；丽丽；冬冬 选的小棒都能搭成长方体或正方体。长、宽、高或棱长各是多少？
（3）请你选择合适的小棒数，计算你所搭长方体的体积是多少？
【分析】（1）根据长方体的特征，长方体是有3组4根同样长的小棒组成；特殊的长方体有两个面是正方形，也就是有8根小棒是相同的，另外4根是相同的，据此判断即可；
（2）根据长方体的特征可知道谁选的小棒都能搭成长方体或正方体；再结合长、宽、高和棱长的定义解答即可；
（3）根据题意选择合适的小棒，再根据长方体的体积公式：V＝abh，据此计算即可。
【解答】解：（1）这些同学选的小棒不都能搭成长方体或正方体，明明的不能，因为长方体是有3组4根同样长的小棒组成的。
（2）我认为聪聪、丽丽和冬冬选的小棒都能搭成长方体或正方体。聪聪的长方体：长为12厘米，宽为10厘米，高为4厘米；丽丽的长方体：长为10厘米，宽为6厘米，高为6厘米；冬冬的正方体：棱长为6厘米。
（3）选择4根12厘米的小棒、4根10厘米的小棒和4根6厘米的小棒。
12×10×6
＝120×6
＝720（立方厘米）
答：长方体的体积是720立方厘米。
故答案为：聪聪；丽丽；冬冬。
【点评】本题考查长方体和正方体的特征，明确它们的特征是解题的关键。
31．某邮政运货车的车厢是长方体，从里面量长8m，宽2.6m，高2m，它的容积是多少立方米？
【分析】首先搞清这道题是求长方体的容积，容积的计算方法和体积是一样的，就用长乘宽再乘高，列式计算即可解决。
【解答】解：8×2.6×2
＝20.8×2
＝41.6（立方米）
答：这个运货车的容积大约是41.6立方米。
【点评】此题主要考查长方体容积的实际应用，长方体的容积计算公式：长方体的容积＝长×宽×高。
32．某海岛战士为解决岛上淡水缺水问题，和当地居民共同修建了一个长22米，宽10米，深1.8米的淡水蓄水池。
（1）这个蓄水池占地有多大？
（2）修建这个蓄水池要挖多少方的泥土？
（3）在四周和底部抹上水泥，抹水泥面积的有多大？
【分析】（1）蓄水池占地的面积就是长方体的底面积，根据长方形的面积公式：S＝ab，据此计算即可；
（2）根据长方体的体积公式：V＝abh，据此计算即可；
（3）求抹水泥面积就是求五个面的面积，根据求五个面的计算方法：S＝（ah+bh）×2+ab，据此进行计算即可。
【解答】解：（1）22×10＝220（平方米）
答：这个蓄水池占地有220平方米。
（2）22×10×1.8
＝220×1.8
＝396（立方米）
答：建这个蓄水池要挖396方的泥土。
（3）（22×1.8+10×1.8）×2+22×10
＝（39.6+18）×2+220
＝57.6×2+220
＝115.2+220
＝335.2（平方米）
答：在四周和底部抹上水泥，抹水泥面积的有335.2平方米。
【点评】本题考查长方体的体积和表面积，熟记公式是解题的关键。
声明：试题解析著作权属所有，未经书面同意，不得复制发布日期：2023/7/28 15:32:45；用户：15290311958；邮箱：15290311958；学号：488613594.8×25%＝
1÷0.125＝
0.13＝
15： ＝
2×a×a＝
m：6dm＝
1﹣+＝
×÷×＝
＝
＝
＝
＝
＝
＝
12厘米
10厘米
6厘米
4厘米
聪聪
4根
4根
4根
明明
6根
6根
丽丽
4根
8根
冬冬
12根
4.8×25%＝
1÷0.125＝
0.13＝
15： 45 ＝
2×a×a＝
m：6dm＝
1﹣+＝
×÷×＝
4.8×25%＝1.2
1÷0.125＝8
0.13＝0.001
15：45＝
2×a×a＝2a²
m：6dm＝dm
1﹣+＝
×÷×＝
＝
＝
＝
＝
＝
＝
＝5÷4＝
＝18÷6＝3
＝22÷7＝3
＝17÷9＝1
＝24÷5＝4
＝40÷8＝5
12厘米
10厘米
6厘米
4厘米
聪聪
4根
4根
4根
明明
6根
6根
丽丽
4根
8根
冬冬
12根