2022-2023学年江西省抚州市临川一中七年级（上）期末数学试卷（含解析）

2022-2023学年江西省抚州市临川一中七年级（上）期末数学试卷

一、选择题（本大题共6小题，共18.0分。在每小题列出的选项中，选出符合题目的一项）

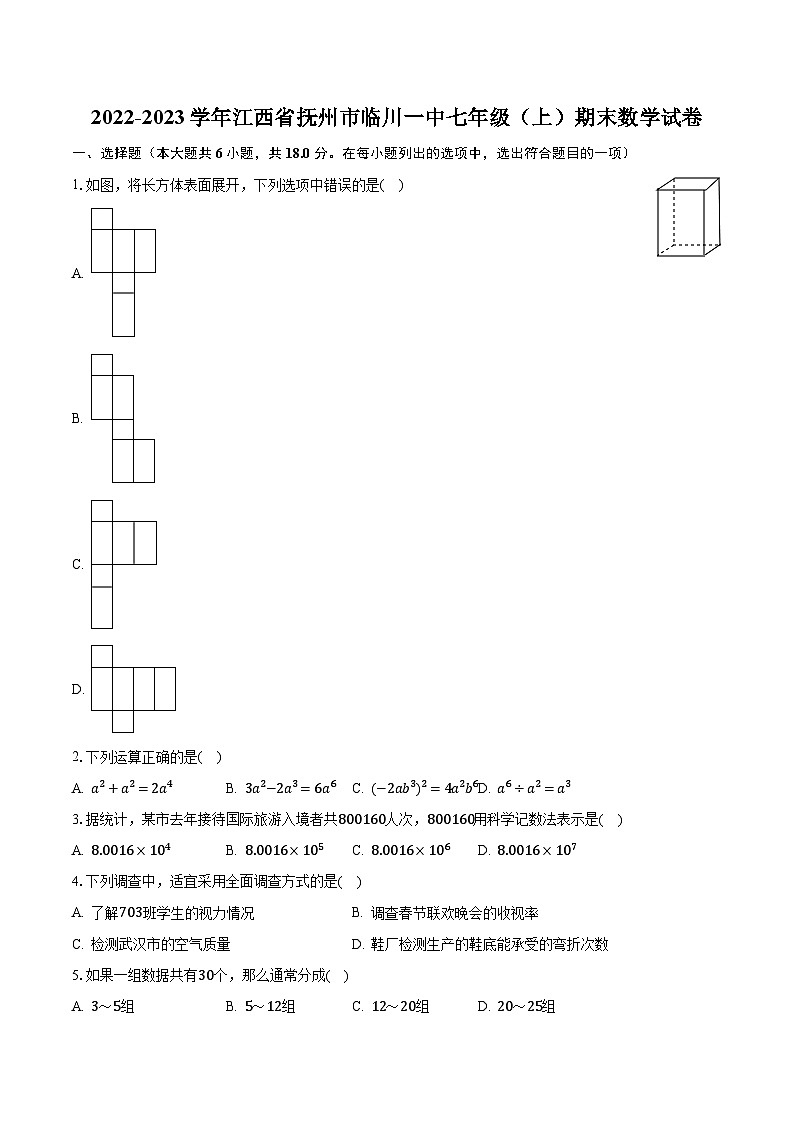
1.如图，将长方体表面展开，下列选项中错误的是(    )

A.
B.
C.
D.

2.下列运算正确的是(    )

A.  B.  C.  D.

3.据统计，某市去年接待国际旅游入境者共人次，用科学记数法表示是(    )

A.  B.  C.  D.

4.下列调查中，适宜采用全面调查方式的是(    )

A. 了解班学生的视力情况 B. 调查春节联欢晚会的收视率
C. 检测武汉市的空气质量 D. 鞋厂检测生产的鞋底能承受的弯折次数

5.如果一组数据共有个，那么通常分成(    )

A. 组 B. 组 C. 组 D. 组

6.点在射线上，若，，为的中点，则为(    )

A.  B.  C.  D.

二、填空题（本大题共6小题，共18.0分）

7.已知、互为相反数，、互为倒数，则的值为______ ．

8.条形统计图能清楚地表示出每个项目的______ ；折线统计图能清楚地反映事物的______ 扇形统计图能清楚地表示出各部分在总体中所占的______ ．

9.已知方程与关于的一元一次方程的解相同，则的值为______ ．

10.时钟上，点时时针与分针的夹角是______．

11.“的倍与的和是非负数”用不等式表示应为______ ．

12.有两根木条，一根长厘米，一根长厘米．如果将它们放在同一条直线上，并且使一个端点重合，这两根木条的中点间的距离是______．

三、解答题（本大题共8小题，共72.0分。解答应写出文字说明，证明过程或演算步骤）

13.本小题分
解方程：
；
 

14.本小题分
某文艺团体为“希望工程”募捐组织了一场义演，共售出张票，筹得票款元．已知学生票元张，成人票元张，问成人票与学生票各售出多少张？

15.本小题分
先化简，再求值：
，其中

16.本小题分
设计一份关于一周内丢弃塑料袋个数的调查问卷，并设计一个抽样调查方案，对全校同学作抽样调查．估计全校同学的家庭一周内共丢弃的塑料袋个数，并根据调查结果估计一个月的情况．

17.本小题分

如图，将一副直角三角板的直角顶点叠放在一起．
如图，若，则 ______ ， ______ ．
如图，猜想与的大小有何特殊关系？并说明理由．
如图，若是两个同样的直角三角板锐角的顶点重合在一起，则与的数量关系为______ ．

18.本小题分
若．
求，的值；
求的值．

19.本小题分
计算
；
．

20.本小题分
如图，已知数轴上点表示的数为，表示的数为，且、满足动点从点出发，以每秒个单位长度的速度沿数轴向左匀速运动，设运动时间为秒．
写出数轴上点表示的数是______，点表示的数是______，点表示的数是______用含的式子表示；
当点在点的左侧运动时，、分别是、的中点，求的值；
动点从点出发，以每秒个单位长度的速度沿数轴向左匀速运动，若点、同时出发，点运动多少秒时、两点相距个单位长度？

答案和解析

1.【答案】 

【解析】【分析】
本题考查的是长方体的展开图，关键是要注意上下底面的长和宽是否可以围成长方体．
长方体的表面展开图的特点，有四个长方形的侧面和上下两个底面组成．
【解答】
解：、是长方体平面展开图，不符合题意；
B、是长方体平面展开图，不符合题意；
C、有两个面重合，不是长方体平面展开图，不符合题意；
D、是长方体平面展开图，不符合题意．
故选C．

2.【答案】 

【解析】解：、，本选项错误．
B、和不是同类项，本选项错误．
C、，本选项正确．
D、，本选项错误．
故选：．
利用合并同类项法则，单项式乘单项式，积的乘方性质同底数幂乘除法判断即可．
本题主要考查合并同类项，单项式乘单项式，积的乘方运算与幂的乘方运算，同底数幂的运算，掌握运算法则是解决此题的关键．

3.【答案】 

【解析】解：．
故选：．
科学记数法的表示形式为的形式，其中，为整数．确定的值是易错点，由于有位，所以可以确定．
此题考查科学记数法表示较大的数的方法，准确确定与值是关键．

4.【答案】 

【解析】【分析】
本题考查了抽样调查和全面调查的区别，选择普查还是抽样调查要根据所要考查的对象的特征灵活选用，一般来说，对于具有破坏性的调查、无法进行普查、普查的意义或价值不大时，应选择抽样调查，对于精确度要求高的调查，事关重大的调查往往选用普查．
由普查得到的调查结果比较准确，但所费人力、物力和时间较多，而抽样调查得到的调查结果比较近似．
【解答】
解：、了解班学生的视力情况，适宜全面调查；
B、调查春节联欢晚会的收视率，适宜采用抽样调查；
C、检测武汉市的空气质量，适宜采用抽样调查；
D、鞋厂检测生产的鞋底能承受的弯折次数，适宜采用抽样调查．
故选：．

5.【答案】 

【解析】解：数据分组的一般方法是：数据的分组时，每组的数目不能太少，若太少的组数，不能反映数据的分布情况；
组数又不能太多，若太多不能反映哪个范围是数值较多，不能正确反映数据的分布．
所以如果一组数据共有个，较合适的是分成组．
故选：．
根据数据分组的一般方法分组即可．
本题考查数据分组，掌握分组的一般方法是解题的关键．

6.【答案】 

【解析】解：如图：

由，，得
，，
为的中点，
．
．
故选：．
根据，，可得和的长；再根据线段中点的性质，可得的长，根据线段的和差，可得的长．
本题考查了两点间的距离．解题的关键是能够正确利用了线段的和差，线段中点的性质．

7.【答案】 

【解析】解：、互为相反数，、互为倒数，
，，
，
故答案为：
根据题意可以求得、的值，从而可以求出题目中所求式子的值．
本题考查有理数混合运算、解答本题的关键是明确有理数混合运算的计算方法．

8.【答案】具体数目  变化情况  百分比 

【解析】解：条形统计图能清楚地表示出每个项目的具体数目；折线统计图能清楚地反映事物的变化情况，扇形统计图能清楚地表示出各部分在总体中所占的百分比．
根据各类统计图的特点即可求出答案．
本题主要考查了条形统计图，扇形统计图和折线统计图的特点．条形统计图能清楚地表示出每个项目的具体数目；折线统计图能清楚地反映事物的变化情况，扇形统计图能清楚地表示出各部分在总体中所占的百分比．

9.【答案】 

【解析】解：，
，
，
，
，
，
由题意得：
把代入方程中得：
，
，
，
，
故答案为：．
先解方程，可得，然后把把代入方程中得：，进行计算即可解答．
本题考查了同解方程，熟练掌握同解方程的意义是解题的关键．

10.【答案】 

【解析】解：九点整，时针和分针中间相差大格．
钟表个数字，每相邻两个数字之间的夹角为，
下午二时正分针与时针的夹角是．
故答案为：．
画出草图，利用钟表表盘的特征解答．
此题考查的知识点是钟面角，用到的知识点为：钟表上个数字，每相邻两个数字之间的夹角为．

11.【答案】 

【解析】解：由题意得：．
故答案为：．
首先表示出的倍与的和为，再表示非负数是：，故可得不等式．
此题主要考查了由实际问题抽象出一元一次不等式，关键是正确理解题意，要抓住题目中的关键词“非负数”正确选择不等号．

12.【答案】或 

【解析】解：若两条线段的另一个端点在重合端点的同旁，则中点间的距离为；
若两条线段的另一个端点在重合端点的异侧，则中点间的距离为．
故答案为：或．
分两种情况：两条线段的另一个端点在重合端点的同旁或异侧．
此题考查两点间的距离，利用线段的和差计算，注意分类讨论．

13.【答案】解：移项得：，
合并同类项得：，
系数化为得：，
去分母得：，
去括号得：，
移项得：，
合并同类项得：，
系数化为得：． 

【解析】依次移项，合并同类项，系数化为，即可得到答案，
依次去分母，去括号，移项，合并同类项，系数化为，即可得到答案．
本题考查了解一元一次方程，正确掌握解一元一次方程的方法是解题的关键．

14.【答案】解：设成人票售出张，则学生票售出张，根据题意可得：，
解得：，
张，
答：成人票售出张，学生票售出张． 

【解析】设成人票售出张，则学生票售出张，根据“票款元”列出方程并解答．
此题主要考查了一元一次方程的应用，理清题里蕴含的数量关系：成人票张数学生票张数张，成人票票款学生票票款是解题关键．

15.【答案】解：

，
当时，
原式． 

【解析】根据整式的化简运算进行化简，再代入即可求解．
此题主要考查整式的化简求值，解题的关键是熟知整式的加减运算法则．

16.【答案】解：一周内家庭丢弃塑料袋个数调查表．

调查方案：发给每班学号是的倍数的同学，一周后收集回来．
估计：将所收集回来的完整数据包含天数据合计部分相加，然后除以统计的学生家庭数，据此可估计全校同学的家庭一周内共丢弃的塑料袋个数；
估计一个月的情况：将以上所得样本的平均数乘以学校学生总人数可得． 

【解析】先选择合适调查方式、制作调查问卷、收集数据、整理数据及对数据的整理和分析求解可得．
本题主要考察调查问卷的设计，调查方案的实施以及对数据的整理和分析等。

17.【答案】     

【解析】解：由题意得：，
，
，
，
故答案为：，；
，理由如下：
，，


；
，理由如下：
，，


．
故答案为：．
由题意可得，，从而可求解；
由，而，从而可求解；
仿照的方法进行求解即可．
本题主要考查角的计算，解答的关键是结合图形分析清楚角与角之间的关系．

18.【答案】解：根据题意得：，
解得：；

原式


． 

【解析】根据非负数的性质：即可非负数的和等于，则每个数等于，据此即可列方程求得和与的值；
把和的值代入，然后把每个式子化成两个分数的差的形式，然后求解．
本题主要考查算术平方根、平方的非负性，解题的关键是要把原分数化成分母相差的两个分数相减，然后才能轻松计算出结果．

19.【答案】解：原式

；

原式
． 

【解析】此题主要考查了有理数的混合运算，正确掌握相关运算法则是解题关键．
直接利用有理数的混合运算法则计算得出答案；
直接利用有理数的混合运算法则计算得出答案．

20.【答案】     

【解析】解：，
，，
，，
点表示的数是，点表示的数是，点表示的数是；
故答案为：，，；
点在点的左侧运动，、分别是、的中点，
表示的数是，表示的数是，
，，
；
动点从点出发，以每秒个单位长度的速度沿数轴向左匀速运动，
表示的数是，
又点表示的数是；
、两点相距个单位长度，
，
或，
解得或，
答：点运动秒或秒时，、两点相距个单位长度．
由可得，，即可得到答案；
表示的数是，表示的数是，可得，，即得；
表示的数是，可得，即可解得答案．
本题考查数轴上的动点问题，解题的关键是用含的代数式表示点运动后表示的数．