山东省菏泽市巨野县麒麟镇第一中学2023-2024学年八年级上学期10月月考数学试题

一、选择题（本大题共10小题，每小题3分，共30分．）

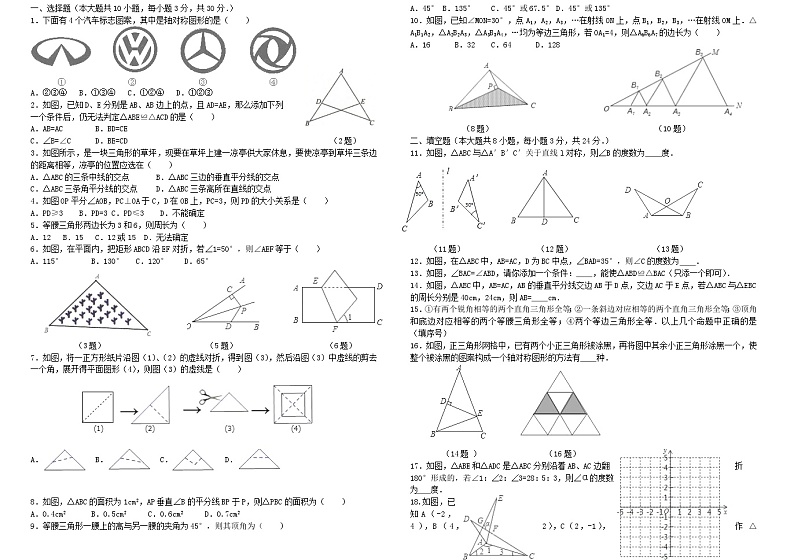
1．下面有4个汽车标志图案，其中是轴对称图形的是（　　）

A．②③④ B．①③④ C．①②④ D．①②③

2．如图，已知D、E分别是AB、AB边上的点，且AD=AE，那么添加下列

一个条件后，仍无法判定△ABE≌△ACD的是（　　）

A．AB=AC     B．BD=CE 

C．∠B=∠C    D．BE=CD                                                  （2题）

3．如图所示，是一块三角形的草坪，现要在草坪上建一凉亭供大家休息，要使凉亭到草坪三条边的距离相等，凉亭的位置应选在（　　）

A．△ABC的三条中线的交点    B．△ABC三边的垂直平分线的交点

C．△ABC三条角平分线的交点    D．△ABC三条高所在直线的交点

4．如图OP平分∠AOB，PC⊥OA于C，D在OB上，PC=3，则PD的大小关系是（　　）

A．PD≥3 B．PD=3 C．PD≤3 D．不能确定

5．等腰三角形两边长为3和6，则周长为（　　）

A．12 B．15 C．12或15 D．无法确定

6．如图，在平面内，把矩形ABCD沿EF对折，若∠1=50°，则∠AEF等于（　　）

A．115°    B．130°   C．120°   D．65°

           （3题）                         （5题）                      （6题）

7．如图，将一正方形纸片沿图（1）、（2）的虚线对折，得到图（3），然后沿图（3）中虚线的剪去一个角，展开得平面图形（4），则图（3）的虚线是（　　）

A． B． C． D．

8．如图，△ABC的面积为1cm2，AP垂直∠B的平分线BP于P，则△PBC的面积为（　　）

A．0.4cm2    B．0.5cm2      C．0.6cm2    D．0.7cm2

9．等腰三角形一腰上的高与另一腰的夹角为45°，则其顶角为（　　）

A．45° B．135° C．45°或67.5° D．45°或135°

10．如图，已知∠MON=30°，点A1，A2，A3，…在射线ON上，点B1，B2，B3，…在射线OM上．△A1B1A2，△A2B2A3，△A3B3A4，…均为等边三角形，若OA1=4，则△A6B6A7的边长为（　　）

A．16    B．32 C．64    D．128

             （8题）                                        （10题）

二、填空题（本大题共8小题，每小题3分，共24分．）

11．如图，△ABC与△A′B′C′关于直线l对称，则∠B的度数为　　度．

     （11题）                  （12题）                    （13题）

12．如图，在△ABC中，AB=AC，D为BC中点，∠BAD=35°，则∠C的度数为　　．

13．如图，∠BAC=∠ABD，请你添加一个条件：　　，能使△ABD≌△BAC（只添一个即可）．

14．如图，△ABC中，AB=AC，AB的垂直平分线交边AB于D点，交边AC于E点，若△ABC与△EBC的周长分别是40cm，24cm，则AB=　　cm．

15．①有两个锐角相等的两个直角三角形全等；②一条斜边对应相等的两个直角三角形全等；③顶角和底边对应相等的两个等腰三角形全等；④两个等边三角形全等．以上几个命题中正确的是　　（填序号）

16．如图，正三角形网格中，已有两个小正三角形被涂黑，再将图中其余小正三角形涂黑一个，使整个被涂黑的图案构成一个轴对称图形的方法有　　种．

        （14题 ）                （16题）                 

17．如图，△ABE和△ADC是△ABC分别沿着AB、AC边翻折180°形成的，若∠1：∠2：∠3=28：5：3，则∠α的度数为　　度．

18.如图，已知A（-2，4），B（4，2），C（2，-1），作△ABC关于x轴的对称图形△A1B1C1，（1）则点C1的坐标          ；
（2）P为x轴上一点，当△PAB的周长最小时的点P的坐标            ．
 

                （17题）                   （18题）

三、解答题（本大题共7小题，共66分．）

19.（8分）如图，AB∥CD，AB=CD，BE=CF，点B，E，F，C

同在一直线上，求证：AF∥DE．
 

20.（10分）如图，要在公路旁修建一个货物中转站，分别向、两个开发区运货．
若要求货站到、两个开发区的距离相等，那么货站应建在那里？
若要求货站到、两个开发区的距离和最小，那么货站应建在那里？
分别在图上找出点和Q，保留作图痕迹，不写作法．
 

21．（8分）如图，已知AB=AC，AD=AE．求证：BD=CE．

22．（14分）如图1，OP是∠MON的平分线，请你利用该图形画一对以OP所在直线为对称轴的全等三角形，并将添加的全等条件标注在图上．

请你参考这个作全等三角形的方法，解答下列问题：

（1）如图2，在△ABC中，∠ACB是直角，∠B=60°，AD、CE分别是∠BAC和∠BCA的平分线，AD、CE相交于点F，求∠EFA的度数；

（2）在（1）的条件下，请判断FE与FD之间的数量关系，并说明理由；

（3）如图3，在△ABC中，如果∠ACB不是直角，而（ 1 ）中的其他条件不变，试问在（2）中所得结论是否仍然成立？若成立，请证明；若不成立，请说明理由．

23.（12分）探究：把两个等腰直角三角板∆ACD与∆BCE如图（1）所示放置，连结AE、BD，AE的延长线交BD于点F。由于∆ACE≌∆DCB,易知AE=BD，AE⊥BD。若两个等腰直角三角板∆ACD与∆BCE如图（2）所示放置，结论（1）AE=BD，（2）AE⊥BD是否仍然成立？请说明理由

24．（14分）如图，已知△ABC中，AB=AC=6cm，∠B=∠C，BC=4cm，点D为AB的中点．如果点P在线段BC上以1cm/s的速度由点B向点C运动，同时，点Q在线段CA上由点C向点A运动．

①若点Q的运动速度与点P的运动速度相等，经过1秒后，△BPD与△CQP是否全等，请说明理由；

②若点Q的运动速度与点P的运动速度不相等，当点Q的运动速度为多少时，能够使△BPD与△CQP全等？

八年级月考数学答案

一、选择题（本大题共10小题，每小题3分，共30分．）

1．D．2．D．3．C．4．A．5．B．

6．A．7．D．8．B．9．D．10．D．

二、填空题（本大题共8小题，每小题3分，共24分．）

11．　100　．12．　55°　．

13．　BD=AC　，答案不唯一14．　16　．15．　③　（填序号）

16．3．17．　80　．18   (2,1)   (2,0)

三、解答题（共6小题，共66分．）

19．（8分）略   20.（10分）略

21．（8分）证明：作AF⊥BC于F，

∵AB=AC（已知），

∴BF=CF（三线合一），

又∵AD=AE（已知），

∴DF=EF（三线合一），

∴BF﹣DF=CF﹣EF，即BD=CE（等式的性质）．

22．（14分）

解：（1）如图2，∵∠ACB=90°，∠B=60°．

∴∠BAC=30°．

∵AD、CE分别是∠BAC和∠BCA的平分线，

∴∠DAC=∠BAC=15°，

∠ECA=∠ACB=45°．

∴∠EFA=∠DAC+∠ECA=15°+45°=60°．

（2）FE=FD．

如图2，在AC上截取AG=AE，连接FG．

∵AD是∠BAC的平分线，

∴∠EAF=∠GAF，

在△EAF和△GAF中

∵

∴△EAF≌△GAF（SAS），

∴FE=FG，∠EFA=∠GFA=60°．

∴∠GFC=180°﹣60°﹣60°=60°．

又∵∠DFC=∠EFA=60°，

∴∠DFC=∠GFC．

在△FDC和△FGC中

∵

∴△FDC≌△FGC（ASA），

∴FD=FG．

∴FE=FD．

（3）（2）中的结论FE=FD仍然成立．

同（2）可得△EAF≌△HAF，

∴FE=FH，∠EFA=∠HFA．

又由（1）知∠FAC=∠BAC，∠FCA=∠ACB，

∴∠FAC+∠FCA=（∠BAC+∠ACB）==60°．

∴∠AFC=180°﹣（∠FAC+∠FCA）=120°．

∴∠EFA=∠HFA=180°﹣120°=60°．

同（2）可得△FDC≌△FHC，

∴FD=FH．

∴FE=FD．

23略

24．解：①全等，理由如下：

∵t=1秒，

∴BP=CQ=1×1=1厘米，

∵AB=6cm，点D为AB的中点，

∴BD=3cm．

又∵PC=BC﹣BP，BC=4cm，

∴PC=4﹣1=3cm，

∴PC=BD．

又∵AB=AC，

∴∠B=∠C，

∴△BPD≌△CQP；

②假设△BPD≌△CQP，

∵vP≠vQ，

∴BP≠CQ，

又∵△BPD≌△CQP，∠B=∠C，则BP=CP=2，BD=CQ=3，

∴点P，点Q运动的时间t==2秒，

∴vQ===1.5cm/s；