安徽省六安市第九中学2023-2024学年八年级上学期第一次月考数学试题

2023-2024学年度九中八上数学第一次综合素质评价

满分：150分时间：120分钟  命题人：未显凤  审题人：王克成

一、单选题（共10小题，满分40分）

1.下列各曲线中不能表示y是x的函数的是（    ）

A.   B.

C.   D.

2.函数中，自变量的取值范围是（    ）

A.   B.   C.   D.

3.直线上有三个点，，，则，，的大小关系是（    ）

A.   B.

C.   D.

4.已知点在第二象限，则直线经过的象限为（    ）

A.一、二、三象限   B.一、三、四象限

C.一、二、四象限   D.二、三、四象限

5.已知点P到x轴的距离为2，到y轴的距离为3，且点P在x轴的上方，则点P的坐标为（    ）

A.（2，3）      B.（3，2）

C.（2，3）或（-2，3）  D.（3，2）或（-3，2）

6.若，则点所在的象限是（    ）

A.第一象限   B.第二象限   C.第三象限   D.第四象限

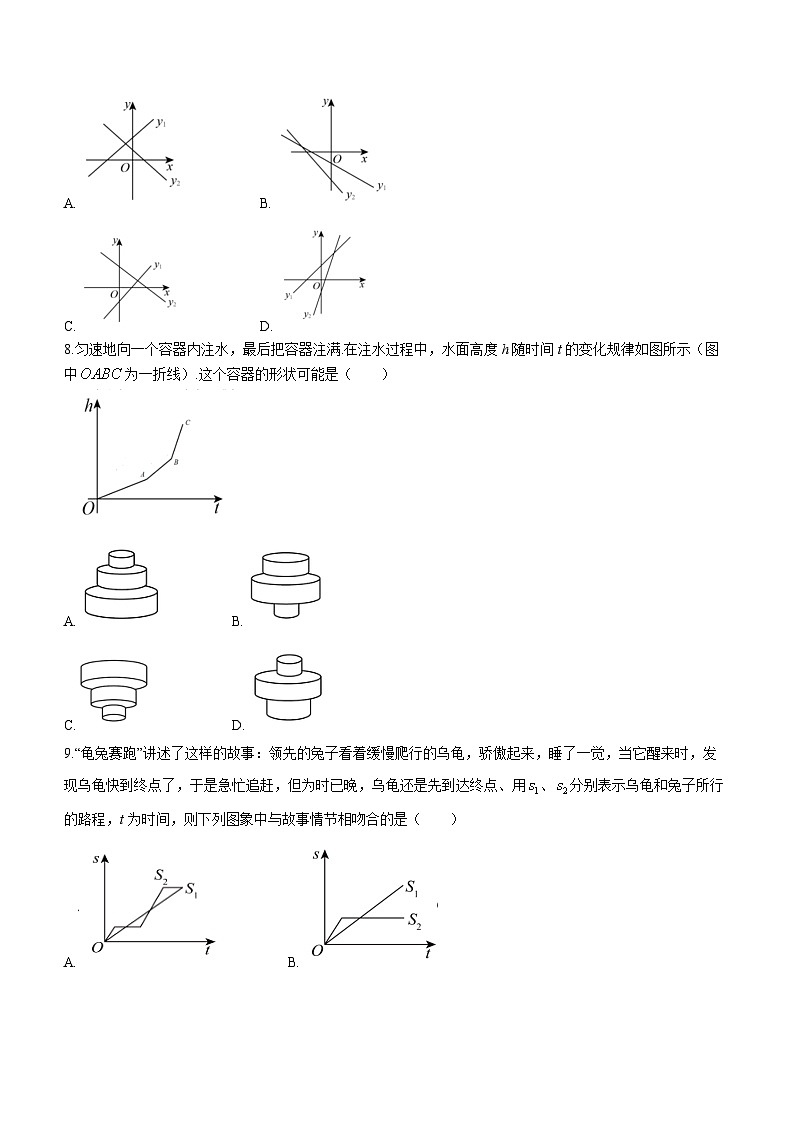
7.一次函数与一次函数在同一平面直角坐标系中的图象大致是（    ）

A.   B.

C.   D.

8.匀速地向一个容器内注水，最后把容器注满.在注水过程中，水面高度h随时间t的变化规律如图所示（图中为一折线）.这个容器的形状可能是（    ）

A.   B.

C.   D.

9.“龟兔赛跑”讲述了这样的故事：领先的兔子看着缓慢爬行的乌龟，骄傲起来，睡了一觉，当它醒来时，发现乌龟快到终点了，于是急忙追赶，但为时已晩，乌龟还是先到达终点、用、分别表示乌龟和兔子所行的路程，t为时间，则下列图象中与故事情节相吻合的是（    ）

A.   B.

C.  D.

10.在平面直角坐标系中，一个智能机器人接到如下指令：从原点O出发，按向右、向上、向右、向下的方向依次不断移动，每次移动1m，其行走路线如图所示，第1次移动到点，第2次移动到点第n次移动到点，则三角形的面积是（    ）

A.   B.   C.   D.

二、填空题（共4小题，满分20分）

11.一次函数的图象与轴交点坐标是__________.

12.在平面直角坐标系内，线段AB平行于x轴，且，若点B的坐标为，则点A的坐标是__________.

13.将点向上平移2个单位得到，且在x轴上，那么点P的坐标是__________.

14.在平面直角坐标系中，已知点和点，且直线AB与坐标轴围成的三角形的面积等于12，则直线AB的解析式为__________.

三、解答题（共4小题，每题8分，共32分）

15.已知点，根据下列条件，求出点A的坐标.

（1）点A在y轴上；

（2）点A到x轴的距离为5.

16.水龙头关闭不严会造成滴水.下表记录了30min内7个时间点的漏水量，其中t表示时间，y表示漏水量.解决下列问题：

（1）结合表中数据，求出滴水量y关于时间t的函数解析式；

（2）在这种漏水状态下，若不及时关闭水龙头，估算一天的漏水量约为多少mL.

17.为让每个农村孩子都能上学，国家实施了“农村中小学寄宿制学校建设工程”，如图是某寄宿制学校的平面示意图，已知旗杆的位置是，实验室的位置是.

（1）请你画出该学校平面示意图所在的坐标系；

（2）办公楼的位置是，教学楼的位置是，在图中标出办公楼和教学楼的位置；

（3）写出食堂、图书馆的坐标.

18.在平面直角坐标系中，一次函数的图象由函数的图象平移得到，且经过点.

（1）求这个一次函数的解析式；

（2）求一次函数的图象与两坐标轴所围成的三角形面积。

四.（共2小题，每题10分，共20分）

19.若与成正比例，且当时，.

（1）求y与x的函数解析式.

（2）求当时，x的值.

20.点P是平面直角坐标系中的一点且不在坐标轴上，过点P向x轴、y轴作垂线段，垂足分别为A、B.若，则点P称为“好点”.例如：点，因为，所以点M是“好点”.

（1）在点，，中，“好点”是_______；

（2）若是“好点”，求的值.

五、（共2题，每题12分，共24分）

21.已知，一次函数.

（1）画出这个函数的图象；

（2）若点在这个函数的图象上，求出的值，写出点的坐标；

（3）若直线与的图象交与y轴上一点，且直线过点，求直线的函数解析式。

22.如图，点A、B、C都在网格格点上，经过平移得到，中任意一点平移后的对应点为.

（1）请在图中作出，并写出点的坐标（__________，__________）.

（2）直接写出的面积：__________；

（3）动点P是坐标轴负半轴上一动点，若使的面积是的面积的2倍，求点P的坐标.

六、（共1题，14分）

23.一辆巡逻车从A地出发沿一条笔直的公路匀速驶向B地，小时后，一辆货车从A地出发，沿同一路线每小时行驶80千米匀速驶向B地，货车到达B地填装货物耗时15分钟，然后立即按原路匀速返回A地.巡逻车、货车离A地的距离y（千米）与货车出发时间x（小时）之间的函数关系如图所示，请结合图象解答下列问题：

（1）A，B两地之间的距离是__________千米，__________；

（2）求线段FG所在直线的函数解析式；

（3）货车出发多少小时两车相距15千米？（直接写出答案即可）

参考答案：

1.C  2.B  3.C  4.C  5.D  6.D  7.A  8.A  9.D  10.C

11.  12.或  13..

14.或

15.（1）解：∵点在上，∴，

解得，

故，

则.

（2）∵点A到x轴的距离为5，∴，则：或，

解得或，

∴或，

∴点A的坐标为或.

16.（1）解：

（2）解：一天的漏水量约为.

17.（1）该学校平面示意图所在的坐标系如图所示，

（2）办公楼和教学楼的位置如图所示，

（3）食堂、图书馆的坐标分别为、.

18.（1）（2）

19.（1）解：设，

把，代入得，解得，

所以，

所以y与x之间的函数关系式为；

（2）当时，，

解答.

20.（1）A和C

（2）

21.（1）解：列表：

描点、连线，画出函数图象；

（2）解：∵点在这个函数的图象上，∴，

解得：，

∴a的值为-4，点Q的坐标为；

（3）

22.（1）点的坐标为（0，2）；（2）5.5；（3）点P的坐标为（-8，0）或

23.（1）解：千米，

∴A，B两地之间的距离是60千米，

∵货车到达B地填装货物耗时15分钟，

∴，

故答案为：60，1

（2）解：设线段FG所在直线的解析式为

将，代入，得

解得，

∴线段FG所在直线的函数解析式为

（3）解：设货车出发x小时两车相距15千米，

由题意得，巡逻车的速度为千米/小时

当两车都在前往B地的途中且未相遇时两车相距15千米，则，

解得（所去）；

当两车都在前往B地的途中且相遇后两车相距15千米，则，

解得；

∵，

∴货车装货过程中两车不可能相距15千米，

当货车从B地前往A地途中且两车未相遇时相距15千米，则，

解得；

当货车从B地前往A地途中且两车相遇后相距15千米，则，

解得；

综上所述，当货车出发小时或小时或小时时，两车相距15千米.