【期中单元复习提升】（沪教版）2023-2024学年六年级数学上册 第一章 数的整除（易错与拓展）测试卷

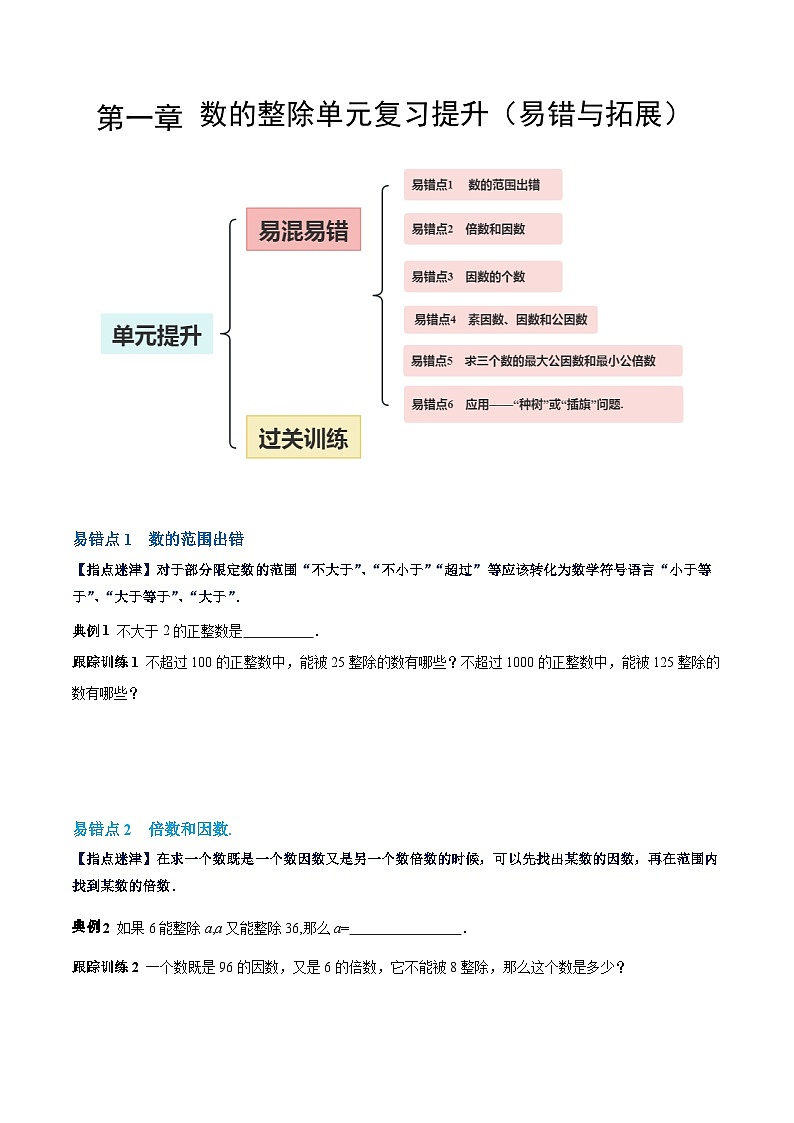
第一章 数的整除单元复习提升（易错与拓展）

易错点1  数的范围出错

【指点迷津】对于部分限定数的范围“不大于”、“不小于”“超过”等应该转化为数学符号语言“小于等于”、“大于等于”、“大于”．

典例1 不大于2的正整数是          ．

错解：1.

错因分析：不大于的意思是小于等于，所以小于等于2的正整数是1,2.

正解：1,2.

跟踪训练1 不超过100的正整数中，能被25整除的数有哪些？不超过1000的正整数中，能被125整除的数有哪些？

【详解】小于等于100的正整数中，25的倍数是25,50,75,100.

小于等于1000的正整数中，125的倍数是125,250,375,500,625,750,875,1000.

易错点2  倍数和因数.

【指点迷津】在求一个数既是一个数因数又是另一个数倍数的时候，可以先找出某数的因数，再在范围内找到某数的倍数．

典例2 如果6能整除a,a又能整除36,那么a=                ．

错解：6.

错因分析：

正解：6,12,18,36.

6能整除a说明要找6的倍数；a又能整除36，说明a是36的因数，那么36的因数又是6的倍数的是：6,12,18,36.

跟踪训练2 一个数既是96的因数，又是6的倍数，它不能被8整除，那么这个数是多少？

【详解】,

所以96的因数有：1，96,2,48,3,32,4,24,6,16,8,12.其中6的倍数：96,48,24,6,12，其中不是8的倍数的是：6,12.

易错点3  因数的个数.

【指点迷津】找一个数的因数既可以通过枚举法列出，也可以通过分解素因数，利用素因数的个数计算得到.

典例3  2016的正因数有__________个.

错解：12.

错因分析：枚举出现错漏.

正解：36

2016=2×2×2×2×2×3×3×7

∴2016的正因数个数：6×3×2=36个

跟踪训练3  1080的正因数有__________.

【答案】32

【详解】1080=2×2×2×3×5×3×3

∴1080的正因数个数：4×4×2=32个

易错点4  素因数、因数和公因数.

【指点迷津】公因数是最大公因数的因数，也是两个数共有的素因数的积；公倍数是最小公倍数的倍数。这几个概念比较容易搞混，需要进行梳理。

典例4 24和36的公因数是__________；24和36的共有的素因数是__________；

错解：12；2、3.

错因分析：只找到最大公因数，没有去找公因数；素因数要写出所有的(包括重复的)

正解：1，2，3，4，6，12；2、2、3.

∵24和36的最大公因数是12，

∴24和36的公因数是1，2，3，4，6，12.

∴24和36的共有的素因数是2、2、3.

跟踪训练4  20和36的公因数是__________；20和36的共有的素因数是__________；

【答案】1，2，4；2，2.

【详解】20=2×2×5；36=2×2×3×3

∴20和36的公因数是1，2，4；

∴20和36的共有的素因数是2、2.

易错点5  求三个数的最大公因数和最小公倍数.

【指点迷津】在求三个数的最大公因数和最小公倍数时需要分两个短除进行，最大公因数需除到三者互素，而最小公倍数需除到两两互素为止.

典例5  56、36和84的最大公因数是____________，最小公倍数是____________.

错解：84；10584.

错因分析：

所以56、36、84的最大公因数是4×7×3=84，最小公倍数是4×14×9×21=10584

正解：

所以56、36、84的最大公因数是4，最小公倍数是4×7×3×3×2=504

跟踪训练5 求下列各组数的最大公因数和最小公倍数．

(1)8、12和30．           (2)16，32和24

【答案】(1)2,120; (2)8,96

【详解】

(1)8、12和30

∴8、12和30的最大公因数是：2，最小公倍数是：2×2×3×2×1×5=120．

(2)8,96

解：∵16=2×2×2×2，32=2×2×2×2×2，24=2×2×2×3，

∴最大公因数是2×2×2=8，

最小公倍数是2×2×2×2×2×3=96．

易错点6  应用——“种树”或“插旗”问题.

【指点迷津】对于“种树”或“插旗”问题，可以先求这些数的最大公因数，再依据不同图形：直线、折线、矩形等进行作图或“掐头去尾”.

典例6 一块矩形地面，长90米，宽15米，要在它的四周和四角种树，每两棵树之间的距离相等，则最少要种______棵树．

错解：12.

错因分析：

正解：14

每两棵树之间的距离要整除90和15，则为90和15的公因数，题目中问最少种多少棵树，则是求90和15的最大公因数，最大公因数为15．则每两棵树之间距离15米种一棵树，一排种7棵树，两排共种14棵树，

故答案为：14．

跟踪训练6一条街道如图所示，长米，长米，长米，要在这条街道的右侧等距离地安装路灯，且要求两端和转弯处都必须装灯，那么这条街道最少要装多少盏灯？

【答案】20盏

【分析】根据要求两端和转弯处都必须装灯，求得与的最大公因数为，根据，，即可求得AB，BC，CD三条街道装的灯的数量，即可求解．

【详解】解：因为，，

与的最大公因数为，

，，

故这条街道最少要装：盏灯．

跟踪训练7 已知某学校六年级学生超过100人，而不足140人．将他们按每组12人分组，多3人；按每组8人分组，也多3人，那么学校六年级学生有________人．

【答案】123

【分析】根据他们按每组12人分组，多3人；按每组8人分组，也多3人，说明总人数减去3就是12和8的公倍数，找出超过100人，而不足140人之内的公倍数即可．

【详解】解：12和8的最小公倍数是24，

12和8的公倍数：24，48，72，96，120，

120+3=123（人），

所以学校六年级学生有123人．

故答案为：123

1、若，，则A和B的最小公倍数是___________．

【答案】210

【分析】两个数公有的质因数和各自独有的质因数乘积是两个数的最小公倍数，据此解答即可．

【详解】解：A=2×3×5，B=3×5×7，

A、B公有的质因数是3和5，

A、B的最小公倍数是：2×5×3×7=210，

故答案为：210．

2、填空：

____________，____________，则M、N的最大公因数是____________，M、N的最小公倍数是____________.

【答案】     24     18     6     72

【分析】根据短除法及最大公因数、最小公倍数可直接进行求解．

【详解】解：由短除法可得：

，，则M、N的最大公因数是，M、N的最小公倍数是；

故答案为24；18；6；72．

3、求下列各组数的最大公因数和最小公倍数．

(1)12和18              (2)24和36                (3)12、15和20

【答案】（1）18与12的最大公约数是6，最小公倍数是36；（2）24与36的最大公约数是12，最小公倍数是72．(3) 最大公约数是1，最小公倍数是60

【分析】(1)(2)都可以用短除法即可得出结果．

【详解】解：(1)12和18的最大公约数：2×3=6，最小公倍数：2×3×2×3=36，

(2) 24与36的最大公约数是2×2×3=12，最小公倍数是2×2×3×2×3=72．

(3) 12=2×2×3，15=3×5，20=2×2×5，

所以12、15和20的最大公因数是1，

最小公倍数是2×2×3×5=60．

4、在下列说法中，正确的是（      ）．

A．奇数都是素数 B．2的倍数都是合数

C．合数不都是偶数 D．5的倍数都是奇数

【答案】C

【分析】根据奇数、偶数、素数、倍数、合数的定义分析，即可完成求解．

【详解】∵15是奇数，但不是素数

故选项A错误；

∵2是2的倍数，但2不是合数

故选项B错误；

∵15是合数，但不是偶数

故选项C正确；

∵，10是偶数

故选项D错误；

故选：C．

5、先求出8和10的最大公因数和最小公倍数，并把最大公因数和最小公倍数相乘，再把8和10相乘，请你观察其中的规律．并用你发现的规律解下面的问题．

（1）甲、乙两数的最大公因数是3，最小公倍数是30，已知甲数是6，则乙数是多少？

（2）甲、乙两数的最大公因数是3，最小公倍数是90，已知甲数是18，则乙数是多少？

【答案】（1）15；（2）15

【分析】观察比较第一个数与第二个数的乘积与最大公因数和最小公倍数的关系，发现：两个正整数的乘积=最大公因数×最小公倍数，据此解答即可．

【详解】解：8×10=80，

8=2×4，

10=2×5，

最大公约数是2，最小公倍数是2×4×5=40，

2×40=80，

我发现了：两个正整数的乘积=最大公因数×最小公倍数．

(1)因为(3×30)÷6=15，所以乙数是15,，

(2)因为(3×90)÷18=15．所以乙数是15，

故答案为：15，15．

6、有三根铁丝，长分别为45米、36米、63米，要把它们都截成同样长的小段，每段长都是整数且不许有剩余，共能截多少个小段？

【答案】共能截144或48或16个小段

【详解】解：因为45、36和63的公因数是1、3和9，

所以可将它们都截成1米长或3米长或9米长的小段，

由于45=1×45=3×15=9×5，

36=1×36=3×12=9×4，

63=1×63=3×21=9×7，

所以当截成1米长的小段时，

共能截45+36+63=144个小段；

当截成3米长的小段时，

共能截15+12+21=48个小段；

当截成9米长的小段时，

共能截5+4+7=16个小段，

答：共能截144或48或16个小段．

7、在1.8千米长的公路一侧有一排电线杆，相邻两根之间距离都是60米．由于电缆的增多，负荷增大，需要把电线杆之间的距离改为45米，起点那根电线杆不动，那么从起点开始到第一根不必移动的电线杆之间的距离是多少？并计算不用移动的电线杆有多少根？

【答案】180米，11根

【分析】由题意可知：不必移动的电线杆距离起点的米数既是45的倍数，又是60的倍数，是45与60的公倍数．45与60的最小公倍数是180，所以至少再隔180米可以有一根电线杆不移动．用公路总长÷180再加1即可求出不用移动的电线杆的数量.

【详解】45＝3×3×5，60＝2×2×3×5，

因为45和60的最小公倍数是：2×2×3×3×5＝180，

所以至少再隔180米又有一根不必移动；

1.8千米=1800米，

1800÷180+1=11（根）

答：从起点开始到第一根不必移动的电线杆之间的距离是180米，不用移动的电线杆有11根．

8、一些贝壳，4个4个地数，最后多1个；5个5个地数，最后多2个；6个6个地数，最后多3个．这些贝壳至少有多少个？

【答案】这些贝壳至少有57个

【分析】根据题意先求出4、5、6的最小公倍数，然后进行求解即可．

【详解】解：，

所以4，5，6的最小公倍数是：，

这些贝壳至少有：（个）．

答：这些贝壳至少有57个．

9、已知甲乙丙三个数，甲和乙的最大公约数是12，甲和丙的最大公约数是15，而三个数的最小公倍数是120，则甲、乙、丙三个数分别是___________________．

【答案】60，24，15或120，12，15

【分析】根据题意得甲是60或120，然后将120分解质因数，分情况讨论即可．

【详解】解：根据题意得：甲的因数有12也有15，那么甲最小是12与15的最小公倍数，

即甲最小是60，又因为三个数最小公倍数是120，

所以甲一定是120的因数，

∴甲是60或120，

把他们的最小公倍数120分解质因数，

，

当甲是60时 ，

所以丙为，

乙为 ，

当甲为120时，乙为 ，

丙为，

∴甲乙丙分别为 60，24，15或120，12，15．