2023年二轮复习解答题专题三：一次函数的应用方案选取型

这是一份2023年二轮复习解答题专题三：一次函数的应用方案选取型，文件包含2023年二轮复习解答题专题三一次函数的应用方案选取型原卷版docx、2023年二轮复习解答题专题三一次函数的应用方案选取型解析版docx等2份试卷配套教学资源，其中试卷共37页， 欢迎下载使用。
2023年二轮复习解答题专题三：
一次函数的应用方案选取型
方法点睛
一次函数应用方案选取型的解题方法
（1） 求函数解析式
根据题干中给出的数据及等量关系,根据待定系数法求出一次函数的解析式.
（2）①根据解析式分类讨论,比较两个方案在不同取值下的最优结果；②根据题意列不等式求出自变量的取值范围,然后选取符合题意的自变量的取值范围,分别代入两个一次函数解析式中比较,最后设计或选择最优方案.
典例分析
类型一 图象型问题
例1 （2022通辽中考）为落实“双减”政策，丰富课后服务的内容，某学校计划到甲、乙两个体育专卖店购买一批新的体育用品，两个商店的优惠活动如下：
甲：所有商品按原价8.5折出售；
乙：一次购买商品总额不超过300元的按原价付费，超过300元的部分打7折．
设需要购买体育用品的原价总额为元，去甲商店购买实付元，去乙商店购买实付元，其函数图象如图所示.

（1）分别求，关于的函数关系式；
（2）两图象交于点，求点坐标；
（3）请根据函数图象，直接写出选择去哪个体育专卖店购买体育用品更合算．
【答案】（1）y甲=0.85x；y乙与x的函数关系式为y乙=
（2）（600，510）
（3）当x＜600时，选择甲商店更合算；当x=600时，两家商店所需费用相同；当x＞600时，选择乙商店更合算．
【解析】
【分析】（1）根据题意，可以分别写出甲、乙两家商店y与x的函数关系式；
（2）根据（1）的结论列方程组解答即可；
（3）由点A的意义并结合图象解答即可．
【小问1详解】
由题意可得，y甲=0.85x；
乙商店：当0≤x≤300时，y乙与x的函数关系式为y乙=x；
当x＞300时，y乙=300+（x-300）×0.7=0.7x+90，
由上可得，y乙与x的函数关系式为y乙=
【小问2详解】
由，解得，
点A的坐标为（600，510）；
【小问3详解】
由点A的意义，当买的体育商品标价为600元时，甲、乙商店优惠后所需费用相同，都是510元，
结合图象可知，
当x＜600时，选择甲商店更合算；
当x=600时，两家商店所需费用相同；
当x＞600时，选择乙商店更合算．
【点睛】本题考查一次函数的应用以及一元一次不等式的应用，解答本题的关键是明确题意，利用一次函数的性质解答．
类型二 文字型问题
例2 （2022宿迁中考）某单位准备购买文化用品，现有甲、乙两家超市进行促销活动，该文化用品两家超市的标价均为10元/件，甲超市一次性购买金额不超过400元的不优惠，超过400元的部分按标价的6折售卖；乙超市全部按标价的8折售卖．
（1）若该单位需要购买30件这种文化用品，则在甲超市的购物金额为 元；乙超市的购物金额为 元；
（2）假如你是该单位的采购员，你认为选择哪家超市支付的费用较少？
【答案】（1）300，240
（2）当时，选择乙超市更优惠，当时，两家超市的优惠一样，当时，选择乙超市更优惠，当时，选择甲超市更优惠．
【解析】
【分析】（1）根据甲、乙两家超市的优惠方案分别进行计算即可；
（2）设单位购买x件这种文化用品，所花费用为y元， 可得当时， 显然此时选择乙超市更优惠，当时 再分三种情况讨论即可．
【小问1详解】
解： 甲超市一次性购买金额不超过400元的不优惠，超过400元的部分按标价的6折售卖；
∴该单位需要购买30件这种文化用品，则在甲超市的购物金额为（元），
∵乙超市全部按标价的8折售卖，
∴该单位需要购买30件这种文化用品，则在甲超市的购物金额为（元），
故答案：
【小问2详解】
设单位购买x件这种文化用品，所花费用为y元，又当10x=400时，可得
当时，
显然此时选择乙超市更优惠，
当时，

当时，则 解得：
∴当时，两家超市的优惠一样，
当时，则 解得：
∴当时，选择乙超市更优惠，
当时，则 解得：
∴当时，选择甲超市更优惠．
【点睛】本题考查的是列代数式，一次函数的实际应用，一元一次不等式的实际应用，清晰的分类讨论是解本题的关键．
专题过关
1. （2022郑州一检）2021年7月24日，中共中央办公厅、国务院办公厅印发《关于进一步减轻义务教育阶段学生作业负担和校外培训负担的意见》．某学校积极响应“双减”政策，为了丰富学生校园生活，经研究决定准备购买一批体育健身器材．已知购买2个篮球和3个排球共花费440元，购买4个篮球和1个排球共花费480元．

（1）求篮球和排球的单价；
（2）某体育用品店有两种优惠方案，方案一：每购买一个篮球就送一个排球；方案二：购买篮球和排球的费用一律打七五折．该学校需要购买40个篮球和x个排球（）．方案一的费用为元，方案二的费用为元．
①根据题目信息，直接写出与x的的函数表达式： ；与x的函数表达式： ；
②画出图象，并直接写出，交点的坐标 ；
③根据图象回答：当购买排球的数量x满足条件 时，方案二比方案一更优惠．
【答案】（1）篮球单价为100元、排球单价为80元；
（2）①y1=80x+800；y2=60x+3000；②（110，9600）；见详解；③x＞110．
【解析】
【分析】（1）设篮球单价为x元、排球单价为y元，根据等量关系购买2个篮球和3个排球共花费440元，购买4个篮球和1个排球共花费480元列二元一次方程组，解方程组即可；
（2）①利用篮球单价×篮球个数+排球单价×优惠后的排球个数得出方案一的费用，利用篮球单价×篮球个数与排球单价×排球个数的和×0,75得出方案二的费用即可；
②用描点法画y2的函数图像，列表，描点，作射线；然后让y1=y2，列方程80x+800=60x+3000，解方程即可；
③根据函数图像，方案二更优惠是方案一的函数图像在方案二的函数图像上方，从而得出当x＞110时，方案二比方案一更优惠．
【小问1详解】
解：设篮球单价为x元、排球单价为y元；
根据题意，得，
解这个方程组得，
篮球单价为100元、排球单价为80元；
【小问2详解】
解：①y1=100×40+80×（x-40）=80x+800，
y2=(100×40+80x)×75%=60x+3000，
故答案为：y1=80x+800；y2=60x+3000；
②列表
x
0
100
y2
3000
9000
描点（0，3000），（100，9000），
过这两点作射线如图，
∵y1=y2，
∴列方程80x+800=60x+3000；
解得x=110，
y1=80×110+800=9600，
∴，交点的坐标（110，9600），
故答案为（110，9600）；

③根据函数图像，方案二更优惠，含义是y1＞y2是指方案一的函数图像在方案二的函数图像上方，
∴当x＞110时，方案二比方案一更优惠．
故答案为x＞110．
【点睛】本题考查列二元一次方程组解应用题，列一次函数解析式，描点法化函数图像，解一元一次方程，利用函数图像求不等式解集．掌握列二元一次方程组解应用题，列一次函数解析式，描点法化函数图像，解一元一次方程，利用函数图像求不等式的解集是解题关键．
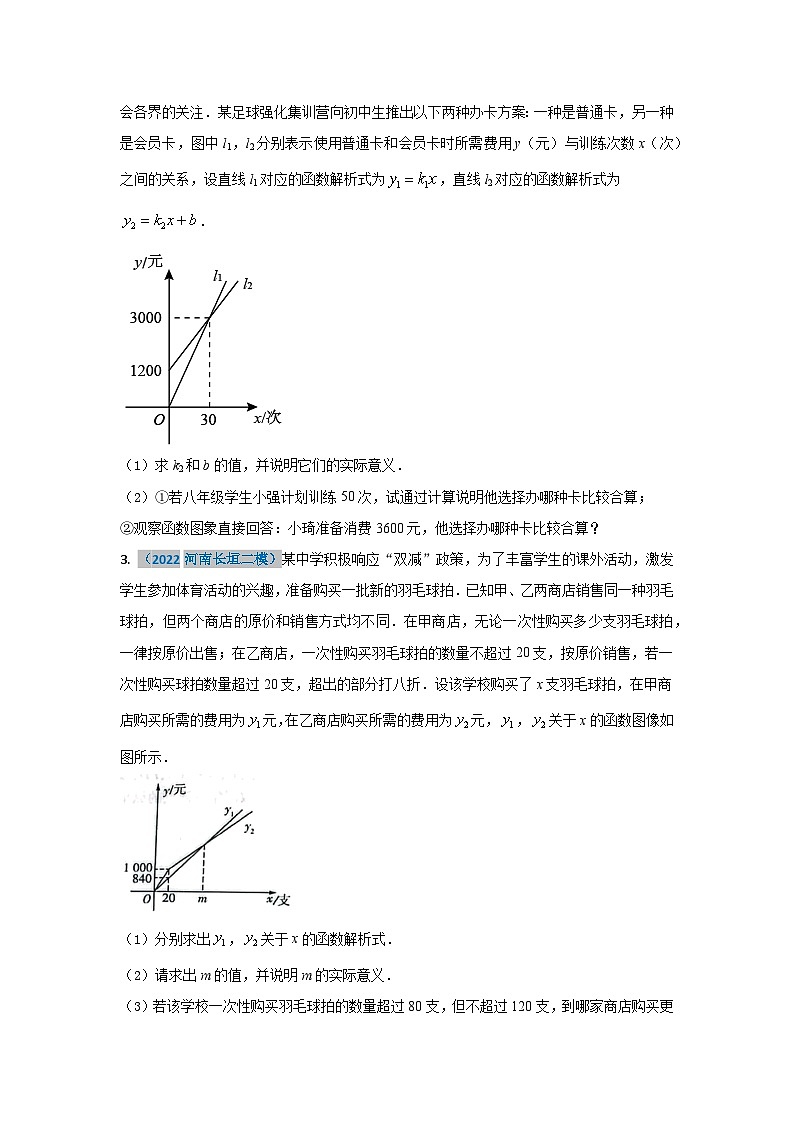
2. （2022河南西华二模）从教育部2021年将足球正式纳入全国中考考核项目后，备受社会各界的关注．某足球强化集训营向初中生推出以下两种办卡方案：一种是普通卡，另一种是会员卡，图中l1，l2分别表示使用普通卡和会员卡时所需费用y（元）与训练次数x（次）之间的关系，设直线l1对应的函数解析式为，直线l2对应的函数解析式为．

（1）求k2和b的值，并说明它们的实际意义．
（2）①若八年级学生小强计划训练50次，试通过计算说明他选择办哪种卡比较合算；
②观察函数图象直接回答：小琦准备消费3600元，他选择办哪种卡比较合算？
【答案】（1），，k2的实际意义为：使用会员卡时所需费用y（元）与训练次数x（次）之间的比例关系，b的实际意义为：办会员卡时需要缴纳的费用
（2）①他选择办会员卡比较合算；②他选择办会员卡比较合算
【解析】
【分析】（1）根据一次函数图像的性质，列二元一次方程组并求解即可；
（2）①根据一次函数的性质计算，即可得到答案；
②根据一次函数图像的性质分析，即可得到答案．
【小问1详解】
根据题意，得：
∴
∴k2的实际意义为：使用会员卡时所需费用y（元）与训练次数x（次）之间的比例关系，b的实际意义为：办会员卡时需要缴纳的费用；
【小问2详解】
①根据（1）的结论，得
根据题意，得：
∴
∴
当时，，
∴
∴八年级学生小强计划训练50次，他选择办会员卡比较合算
②根据图像，得：消费3600元时，，即小琦办理会员卡，可以训练的次数更多
∴小琦准备消费3600元，他选择办会员卡比较合算．
【点睛】本题考查了一次函数、二元一次方程组的知识；解题的关键是熟练掌握一次函数的性质，从而完成求解．
3. （2022河南长垣二模）某中学积极响应“双减”政策，为了丰富学生的课外活动，激发学生参加体育活动的兴趣，准备购买一批新的羽毛球拍．已知甲、乙两商店销售同一种羽毛球拍，但两个商店的原价和销售方式均不同．在甲商店，无论一次性购买多少支羽毛球拍，一律按原价出售；在乙商店，一次性购买羽毛球拍的数量不超过20支，按原价销售，若一次性购买球拍数量超过20支，超出的部分打八折．设该学校购买了x支羽毛球拍，在甲商店购买所需的费用为元，在乙商店购买所需的费用为元，，关于x的函数图像如图所示．

（1）分别求出，关于x的函数解析式．
（2）请求出m的值，并说明m的实际意义．
（3）若该学校一次性购买羽毛球拍的数量超过80支，但不超过120支，到哪家商店购买更优惠？
【答案】（1）；
（2）m=100，m的实际意义是当一次性购买羽毛球球拍的数量100支时，甲、乙商店所需费用相同，都为4200元
（3）当80