
黑龙江省鸡西市2021-2023三年中考数学真题分类汇编-01选择题知识点分类
展开黑龙江省鸡西市2021-2023三年中考数学真题分类汇编-01选择题知识点分类
一.科学记数法—表示较大的数(共1小题)
1.(2022•黑龙江)据测算,世博会召开时,上海使用清洁能源可减少二氧化碳排放约16万吨,将16万吨用科学记数法表示为( )
A.1.6×103吨 B.1.6×104吨 C.1.6×105吨 D.1.6×106吨
二.同底数幂的乘法(共1小题)
2.(2021•黑龙江)下列运算正确的是( )
A.﹣3﹣2=﹣1 B.3×(﹣)2=﹣
C.x3•x5=x15 D.•=a
三.平方差公式(共1小题)
3.(2023•黑龙江)下列运算正确的是( )
A.(﹣2a)2=﹣4a2 B.(a﹣b)2=a2﹣b2
C.(﹣m+2)(﹣m﹣2)=m2﹣4 D.(a5)2=a7
四.二元一次方程的应用(共1小题)
4.(2023•黑龙江)某社区为了打造“书香社区”,丰富小区居民的业余文化生活,计划出资500元全部用于采购A,B,C三种图书,A种每本30元,B种每本25元,C种每本20元,其中A种图书至少买5本,最多买6本(三种图书都要买),此次采购的方案有( )
A.5种 B.6种 C.7种 D.8种
五.一元二次方程的一般形式(共1小题)
5.(2021•黑龙江)关于x的一元二次方程(m﹣3)x2+m2x=9x+5化为一般形式后不含一次项,则m的值为( )
A.0 B.±3 C.3 D.﹣3
六.根的判别式(共1小题)
6.(2022•黑龙江)下列方程没有实数根的是( )
A.x2+4x=10 B.3x2+8x﹣3=0
C.x2﹣2x+3=0 D.(x﹣2)(x﹣3)=12
七.一元二次方程的应用(共1小题)
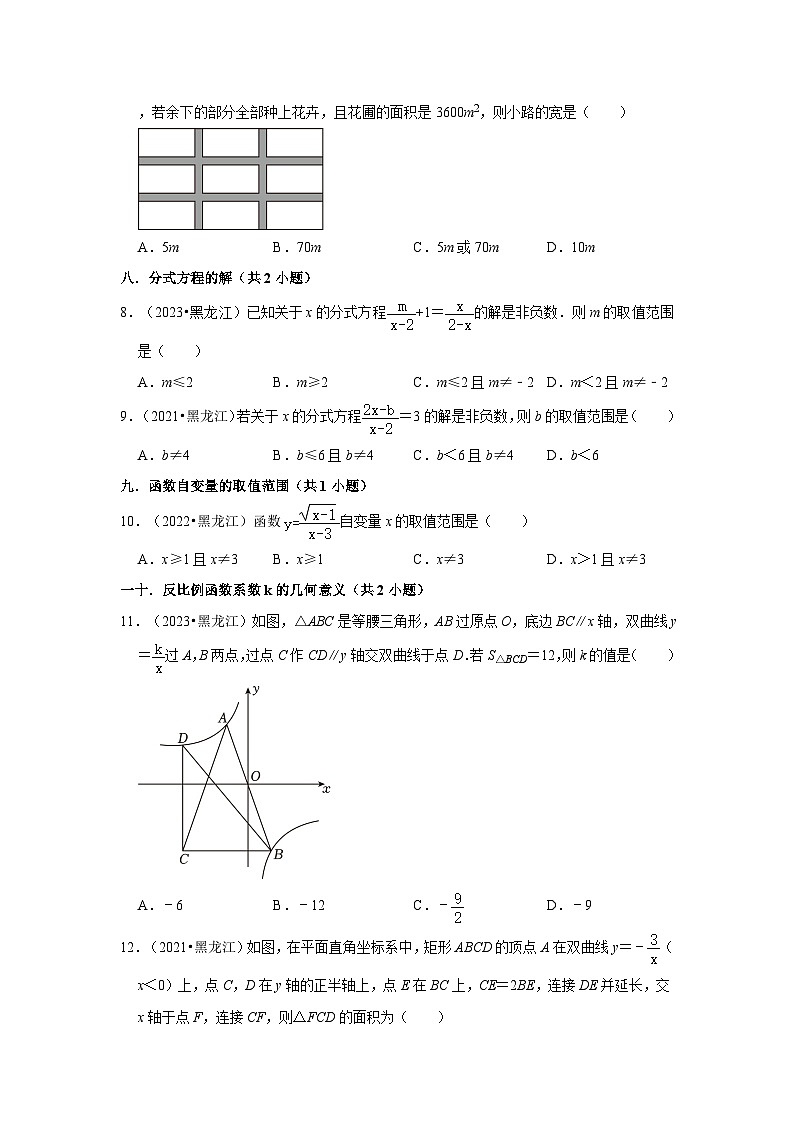
7.(2023•黑龙江)如图,在长为100m,宽为50m的矩形空地上修筑四条宽度相等的小路,若余下的部分全部种上花卉,且花圃的面积是3600m2,则小路的宽是( )
A.5m B.70m C.5m或70m D.10m
八.分式方程的解(共2小题)
8.(2023•黑龙江)已知关于x的分式方程+1=的解是非负数.则m的取值范围是( )
A.m≤2 B.m≥2 C.m≤2且m≠﹣2 D.m<2且m≠﹣2
9.(2021•黑龙江)若关于x的分式方程=3的解是非负数,则b的取值范围是( )
A.b≠4 B.b≤6且b≠4 C.b<6且b≠4 D.b<6
九.函数自变量的取值范围(共1小题)
10.(2022•黑龙江)函数自变量x的取值范围是( )
A.x≥1且x≠3 B.x≥1 C.x≠3 D.x>1且x≠3
一十.反比例函数系数k的几何意义(共2小题)
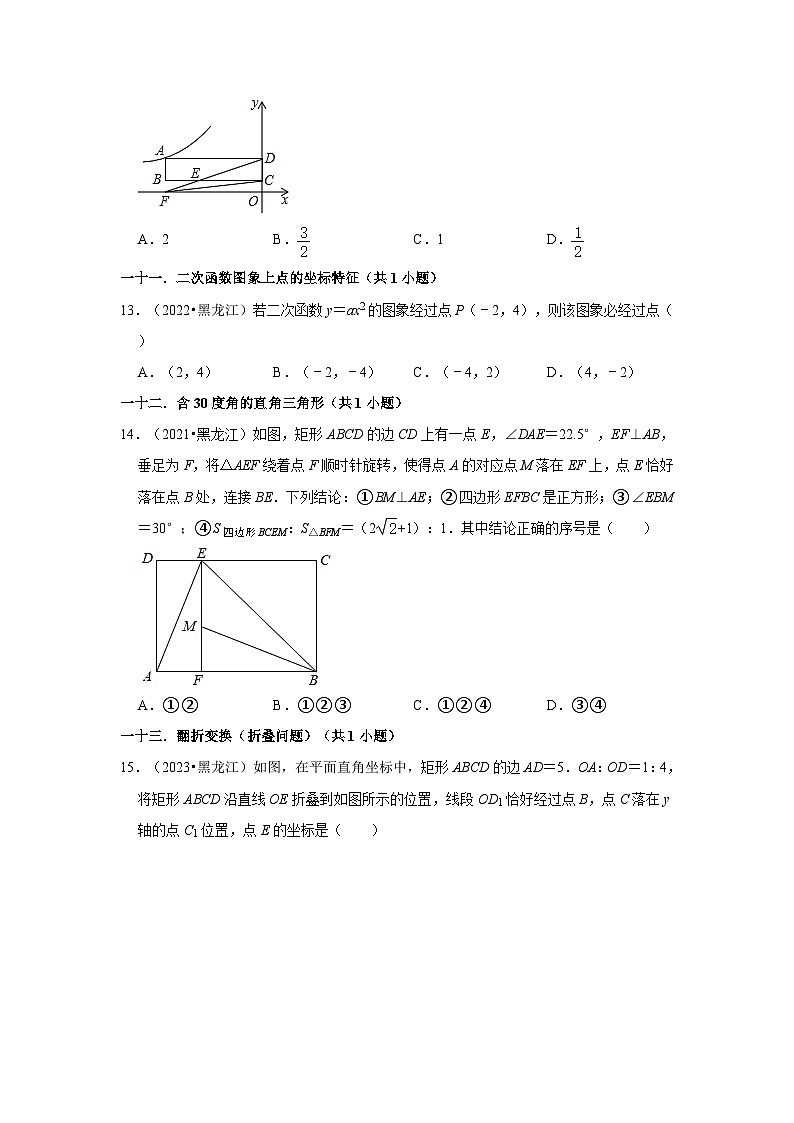
11.(2023•黑龙江)如图,△ABC是等腰三角形,AB过原点O,底边BC∥x轴,双曲线y=过A,B两点,过点C作CD∥y轴交双曲线于点D.若S△BCD=12,则k的值是( )
A.﹣6 B.﹣12 C.﹣ D.﹣9
12.(2021•黑龙江)如图,在平面直角坐标系中,矩形ABCD的顶点A在双曲线y=﹣(x<0)上,点C,D在y轴的正半轴上,点E在BC上,CE=2BE,连接DE并延长,交x轴于点F,连接CF,则△FCD的面积为( )
A.2 B. C.1 D.
一十一.二次函数图象上点的坐标特征(共1小题)
13.(2022•黑龙江)若二次函数y=ax2的图象经过点P(﹣2,4),则该图象必经过点( )
A.(2,4) B.(﹣2,﹣4) C.(﹣4,2) D.(4,﹣2)
一十二.含30度角的直角三角形(共1小题)
14.(2021•黑龙江)如图,矩形ABCD的边CD上有一点E,∠DAE=22.5°,EF⊥AB,垂足为F,将△AEF绕着点F顺时针旋转,使得点A的对应点M落在EF上,点E恰好落在点B处,连接BE.下列结论:①BM⊥AE;②四边形EFBC是正方形;③∠EBM=30°;④S四边形BCEM:S△BFM=(2+1):1.其中结论正确的序号是( )
A.①② B.①②③ C.①②④ D.③④
一十三.翻折变换(折叠问题)(共1小题)
15.(2023•黑龙江)如图,在平面直角坐标中,矩形ABCD的边AD=5.OA:OD=1:4,将矩形ABCD沿直线OE折叠到如图所示的位置,线段OD1恰好经过点B,点C落在y轴的点C1位置,点E的坐标是( )
A.(1,2) B.(﹣1,2) C.(﹣1,2) D.(1﹣,2)
一十四.中心对称图形(共3小题)
16.(2023•黑龙江)下列新能源汽车标志图案中,既是轴对称图形,又是中心对称图形的是( )
A. B.
C. D.
17.(2022•黑龙江)下列图形中是轴对称图形但不是中心对称图形的是( )
A. B. C. D.
18.(2021•黑龙江)下列图形中,既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.
一十五.相似三角形的判定与性质(共1小题)
19.(2023•黑龙江)如图,在正方形ABCD中,点E,F分别是AB,BC上的动点,且AF⊥DE,垂足为G,将△ABF沿AF翻折,得到△AMF,AM交DE于点P,对角线BD交AF于点H,连接HM,CM,DM,BM,下列结论正确的是( )
①AF=DE;②BM∥DE;③若CM⊥FM,则四边形BHMF是菱形;④当点E运动到AB的中点,tan∠BHF=2;⑤EP•DH=2AG•BH.
A.①②③④⑤ B.①②③⑤ C.①②③ D.①②⑤
一十六.解直角三角形(共1小题)
20.(2021•黑龙江)如图,在△ABC中,∠ACB=90°,点D在AB的延长线上,连接CD,若AB=2BD,tan∠BCD=,则的值为( )
A.1 B.2 C. D.
一十七.解直角三角形的应用-坡度坡角问题(共1小题)
21.(2022•黑龙江)小明去爬山,在山脚看山顶角度为30°,小明在坡比为5:12的山坡上走1300米,此时小明看山顶的角度为60°,山高为( )米
A.600﹣250 B.600﹣250 C.350+350 D.500
一十八.由三视图判断几何体(共3小题)
22.(2023•黑龙江)一个由若干个大小相同的小正方体搭成的几何体,它的俯视图和左视图如图所示,那么组成该几何体所需小正方体的个数最少是( )
A.4 B.5 C.6 D.7
23.(2022•黑龙江)如图是一些完全相同的小正方体搭成的几何体的三视图.这个几何体只能是( )
A. B. C. D.
24.(2021•黑龙江)由若干个完全相同的小立方块搭成的几何体的左视图和俯视图如图所示,则搭成该几何体所用的小立方块的个数可能是( )
A.4个 B.5个 C.7个 D.8个
一十九.频数与频率(共1小题)
25.(2022•黑龙江)王老师对本班40名学生的血型作了统计,列出如下的统计表,则本班A型血的人数是( )
组别
A型
B型
AB型
O型
频率
0.4
0.35
0.1
0.15
A.16人 B.14人 C.4人 D.6人
二十.中位数(共1小题)
26.(2022•黑龙江)一组数据13,10,10,11,16的中位数和平均数分别是( )
A.11,13 B.11,12 C.13,12 D.10,12
二十一.众数(共2小题)
27.(2023•黑龙江)已知一组数据1,0,﹣3,5,x,2,﹣3的平均数是1,则这组数据的众数是( )
A.﹣3 B.5 C.﹣3和5 D.1和3
28.(2021•黑龙江)从小到大的一组数据﹣1,1,2,x,6,8的中位数为2,则这组数据的众数和平均数分别是( )
A.2,4 B.2,3 C.1,4 D.1,3
二十二.列表法与树状图法(共1小题)
29.(2022•黑龙江)袋子里有4个球,标有2,3,4,5,先抽取一个并记住,放回,然后再抽取一个,所抽取的两个球数字之和大于6的概率是( )
A. B. C. D.
二十三.排列与组合问题(共1小题)
30.(2021•黑龙江)大课间,12人跳绳队为尊重每个队员的意愿,准备把队员分成跳大绳组或跳小绳组,大绳组3人一组,小绳组2人一组,在全队同学能同时参加活动且符合小组规定人数的前提下,则不同的分组方法有( )
A.1种 B.2种 C.3种 D.4种
黑龙江省鸡西市2021-2023三年中考数学真题分类汇编-01选择题知识点分类
参考答案与试题解析
一.科学记数法—表示较大的数(共1小题)
1.(2022•黑龙江)据测算,世博会召开时,上海使用清洁能源可减少二氧化碳排放约16万吨,将16万吨用科学记数法表示为( )
A.1.6×103吨 B.1.6×104吨 C.1.6×105吨 D.1.6×106吨
【答案】C
【解答】解:将16万吨用科学记数法表示为:1.6×105吨.
故选:C.
二.同底数幂的乘法(共1小题)
2.(2021•黑龙江)下列运算正确的是( )
A.﹣3﹣2=﹣1 B.3×(﹣)2=﹣
C.x3•x5=x15 D.•=a
【答案】D
【解答】解:A、﹣3﹣2=﹣5,故此选项错误;
B、3×(﹣)2=,故此选项错误;
C、x3•x5=x8,故此选项错误;
D、•=a,正确.
故选:D.
三.平方差公式(共1小题)
3.(2023•黑龙江)下列运算正确的是( )
A.(﹣2a)2=﹣4a2 B.(a﹣b)2=a2﹣b2
C.(﹣m+2)(﹣m﹣2)=m2﹣4 D.(a5)2=a7
【答案】C
【解答】解:(﹣2a)2=4a2,所以A错误;
(a﹣b)2=a2﹣2ab+b2,所以B错误;
(﹣m+2)(﹣m﹣2)=m2﹣4,所以C正确;
(a5)2=a10,所以D错误.
故选:C.
四.二元一次方程的应用(共1小题)
4.(2023•黑龙江)某社区为了打造“书香社区”,丰富小区居民的业余文化生活,计划出资500元全部用于采购A,B,C三种图书,A种每本30元,B种每本25元,C种每本20元,其中A种图书至少买5本,最多买6本(三种图书都要买),此次采购的方案有( )
A.5种 B.6种 C.7种 D.8种
【答案】B
【解答】解:当购买5本A种图书时,设购买x本B种图书,y本C种图书,
根据题意得:30×5+25x+20y=500,
∴x=14﹣y,
又∵x,y均为正整数,
∴或或,
∴当购买5本A种图书时,有3种采购方案;
当购买6本A种图书时,设购买m本B种图书,n本C种图书,
根据题意得:30×6+25m+20n=500,
∴n=16﹣m,
又∵m,n均为正整数,
∴或或,
∴当购买6本A种图书时,有3种采购方案.
∴此次采购的方案有3+3=6(种).
故选:B.
五.一元二次方程的一般形式(共1小题)
5.(2021•黑龙江)关于x的一元二次方程(m﹣3)x2+m2x=9x+5化为一般形式后不含一次项,则m的值为( )
A.0 B.±3 C.3 D.﹣3
【答案】D
【解答】解:(m﹣3)x2+m2x=9x+5,
(m﹣3)x2+(m2﹣9)x﹣5=0,
由题意得:m﹣3≠0,m2﹣9=0,
解得:m=﹣3,
故选:D.
六.根的判别式(共1小题)
6.(2022•黑龙江)下列方程没有实数根的是( )
A.x2+4x=10 B.3x2+8x﹣3=0
C.x2﹣2x+3=0 D.(x﹣2)(x﹣3)=12
【答案】C
【解答】解:A、方程变形为:x2+4x﹣10=0,Δ=42﹣4×1×(﹣10)=56>0,所以方程有两个不相等的实数根,故A选项不符合题意;
B、Δ=82﹣4×3×(﹣3)=100>0,所以方程有两个不相等的实数根,故B选项不符合题意;
C、Δ=(﹣2)2﹣4×1×3=﹣8<0,所以方程没有实数根,故C选项符合题意;
D、方程变形为:x2﹣5x﹣6=0,Δ=52﹣4×1×(﹣6)=49>0,所以方程有两个不相等的实数根,故D选项不符合题意.
故选:C.
七.一元二次方程的应用(共1小题)
7.(2023•黑龙江)如图,在长为100m,宽为50m的矩形空地上修筑四条宽度相等的小路,若余下的部分全部种上花卉,且花圃的面积是3600m2,则小路的宽是( )
A.5m B.70m C.5m或70m D.10m
【答案】A
【解答】解:设小路的宽是xm,则余下的部分可合成长为(100﹣2x)m,宽为(50﹣2x)m的矩形,
根据题意得:(100﹣2x)(50﹣2x)=3600,
整理得:x2﹣75x+350=0,
解得:x1=5,x2=70(不符合题意,舍去),
∴小路的宽是5m.
故选:A.
八.分式方程的解(共2小题)
8.(2023•黑龙江)已知关于x的分式方程+1=的解是非负数.则m的取值范围是( )
A.m≤2 B.m≥2 C.m≤2且m≠﹣2 D.m<2且m≠﹣2
【答案】C
【解答】解:分式方程去分母得:m+x﹣2=﹣x,
解得:x=,
由分式方程的解是非负数,得到≥0,且﹣2≠0,
解得:m≤2且m≠﹣2,
故选:C.
9.(2021•黑龙江)若关于x的分式方程=3的解是非负数,则b的取值范围是( )
A.b≠4 B.b≤6且b≠4 C.b<6且b≠4 D.b<6
【答案】B
【解答】解:去分母得,2x﹣b=3x﹣6,
∴x=6﹣b,
∵x≥0,
∴6﹣b≥0,
解得,b≤6,
又∵x﹣2≠0,
∴x≠2,
即6﹣b≠2,b≠4,
则b的取值范围是b≤6且b≠4,
故选:B.
九.函数自变量的取值范围(共1小题)
10.(2022•黑龙江)函数自变量x的取值范围是( )
A.x≥1且x≠3 B.x≥1 C.x≠3 D.x>1且x≠3
【答案】A
【解答】解:根据题意得,x﹣1≥0且x﹣3≠0,
解得x≥1且x≠3.
故选:A.
一十.反比例函数系数k的几何意义(共2小题)
11.(2023•黑龙江)如图,△ABC是等腰三角形,AB过原点O,底边BC∥x轴,双曲线y=过A,B两点,过点C作CD∥y轴交双曲线于点D.若S△BCD=12,则k的值是( )
A.﹣6 B.﹣12 C.﹣ D.﹣9
【答案】C
【解答】解:设BC与y轴的交点为F,B(b,),则A(﹣b,﹣),b>0,由题意知,
AO=BO,即O是线段AB的中点,过A作AE⊥BC于点E,
∵AC=AB,AE⊥BC,
∴BE=CE,AE∥y轴,
∴CF=3BF=3b,
∴C(﹣3b,),
∴D(﹣3b,),
∴CD=,BC=4b,
∴S△BCD=,
∴k=﹣.
故选:C.
12.(2021•黑龙江)如图,在平面直角坐标系中,矩形ABCD的顶点A在双曲线y=﹣(x<0)上,点C,D在y轴的正半轴上,点E在BC上,CE=2BE,连接DE并延长,交x轴于点F,连接CF,则△FCD的面积为( )
A.2 B. C.1 D.
【答案】C
【解答】解:根据题意,设A(n,﹣),D(0,﹣),
设OC=m,则C(0,m),CD=﹣﹣m,
∴B(n,m),BC=﹣n,
∵CE=2BE,
∴CE=BC=﹣n,
∴E(n,m),
由题知BC∥FO,
∴∠DEC=∠DFO,∠DCE=∠DOF,
∴△DEC∽△DFO,
∴=,
即=,
∴FO=,
∴S△FCD=FO•CD=×(﹣﹣m)=1,
故选:C.
一十一.二次函数图象上点的坐标特征(共1小题)
13.(2022•黑龙江)若二次函数y=ax2的图象经过点P(﹣2,4),则该图象必经过点( )
A.(2,4) B.(﹣2,﹣4) C.(﹣4,2) D.(4,﹣2)
【答案】A
【解答】解:∵二次函数y=ax2的对称轴为y轴,
∴若图象经过点P(﹣2,4),
则该图象必经过点(2,4).
故选:A.
一十二.含30度角的直角三角形(共1小题)
14.(2021•黑龙江)如图,矩形ABCD的边CD上有一点E,∠DAE=22.5°,EF⊥AB,垂足为F,将△AEF绕着点F顺时针旋转,使得点A的对应点M落在EF上,点E恰好落在点B处,连接BE.下列结论:①BM⊥AE;②四边形EFBC是正方形;③∠EBM=30°;④S四边形BCEM:S△BFM=(2+1):1.其中结论正确的序号是( )
A.①② B.①②③ C.①②④ D.③④
【答案】C
【解答】解:如图,延长BM交AE于N,连接AM,
∵EF⊥AB,
∴∠AFE=∠EFB=90°,
∵∠DAE=22.5°,
∴∠EAF=90°﹣∠DAE=67.5°,
∵将△AEF绕着点F顺时针旋转得△MFB,
∴MF=AF,FB=FE,∠FBM=∠AEF=∠DAE=22.5°,
∴∠EAF+∠FBM=90°,
∴∠ANB=90°,
∴BM⊥AE,故①正确;
∵四边形ABCD是矩形,
∴∠ABC=∠C=90°,
∵∠EFB=90°,
∴四边形EFBC是矩形,
又∵EF=BF,
∴矩形EFBC是正方形,故②正确;
∴∠EBF=45°,
∴∠EBM=∠EBF﹣∠FBM
=45°﹣22.5°
=22.5°,
故③错误;
∵∠AFM=90°,AF=FM,
∴∠MAF=45°,AM=,
∴∠EAM=67.5°﹣45°=22.5°,
∴∠AEM=∠MAE,
∴EM=AM=FM,
∴EF=EM+FM=(+1)FM,
∴S△EFB:S△BFM=( ):1,
又∵四边形BCEF是正方形,
∴S四边形BCEF=2S△EFB,
∴S四边形BCEM:S△BFM=(2+1):1,
故④正确,
∴正确的是:①②④,
故选:C.
一十三.翻折变换(折叠问题)(共1小题)
15.(2023•黑龙江)如图,在平面直角坐标中,矩形ABCD的边AD=5.OA:OD=1:4,将矩形ABCD沿直线OE折叠到如图所示的位置,线段OD1恰好经过点B,点C落在y轴的点C1位置,点E的坐标是( )
A.(1,2) B.(﹣1,2) C.(﹣1,2) D.(1﹣,2)
【答案】D
【解答】解:∵矩形ABCD的边AD=5.OA:OD=1:4,
∴OA=1,OD=4,BC=5,
∵AB∥OC1,
∴∠ABO=∠D1OC1,
∵∠BAO=∠OD1C1=90°,
∴△AOB∽△D1C1O,
∴,
∵将矩形ABCD沿直线OE折叠到如图所示的位置,
∴OD1=OD=4,D1C1=DC=AB,
∴,
∴AB=2(负值舍去),
∴CD=2,
连接OC,设BC与OC1交于F,
∴OC=,
∵∠FOA=∠OAB=∠ABF=90°,
∴四边形OABF是矩形,
∴AB=OF=2,∠BFO=90°=∠EFC1,OA=BF=1,
∴CF=5﹣1=4,
由折叠知,OC1=OC=2,EC1=EC=CF﹣EF=4﹣EF,
∴FC1=OC1=2﹣2,
∵EF2+C1F2=,
∴,
解得EF=﹣1,
∴E(1﹣,2),
故选:D.
一十四.中心对称图形(共3小题)
16.(2023•黑龙江)下列新能源汽车标志图案中,既是轴对称图形,又是中心对称图形的是( )
A. B.
C. D.
【答案】A
【解答】解:A、既是轴对称图形,又是中心对称图形,故A符合题意;
B、D,是轴对称图形,但不是中心对称图形,故B、D不符合题意;
C、不是轴对称图形,是中心对称图形.故C不符合题意.
故选:A.
17.(2022•黑龙江)下列图形中是轴对称图形但不是中心对称图形的是( )
A. B. C. D.
【答案】B
【解答】解:A、图形不是中心对称轴图形,也不是轴对称图形,此选项错误;
B、图形不是中心对称轴图形,是轴对称图形,此选项正确;
C、图形是中心对称轴图形,也是轴对称图形,此选项错误;
D、图形是中心对称轴图形,不是轴对称图形,此选项错误;
故选:B.
18.(2021•黑龙江)下列图形中,既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.
【答案】C
【解答】解:A选项是轴对称图形,不是中心对称图形,不符合题意;
B选项是轴对称图形,不是中心对称图形,不符合题意;
C选项既是轴对称图形,又是中心对称图形,符合题意;
D选项不是轴对称图形,是中心对称图形,不符合题意;
故选:C.
一十五.相似三角形的判定与性质(共1小题)
19.(2023•黑龙江)如图,在正方形ABCD中,点E,F分别是AB,BC上的动点,且AF⊥DE,垂足为G,将△ABF沿AF翻折,得到△AMF,AM交DE于点P,对角线BD交AF于点H,连接HM,CM,DM,BM,下列结论正确的是( )
①AF=DE;②BM∥DE;③若CM⊥FM,则四边形BHMF是菱形;④当点E运动到AB的中点,tan∠BHF=2;⑤EP•DH=2AG•BH.
A.①②③④⑤ B.①②③⑤ C.①②③ D.①②⑤
【答案】B
【解答】解:∵四边形ABCD是正方形,
∴∠DAE=∠ABF=90°,DA=AB,
∵AF⊥DE,
∴∠BAF+∠AED=90°,
∵∠BAF+∠AFB=90°,
∴∠AED=∠BFA,
在△ABF和△DAE中,
,
∴△ABF≌△DAE(AAS),
∴AF=DE.
故①正确;
∵将△ABF沿AF翻折,得到△AMF,
∴BM⊥AF,
∵AF⊥DE,
∴BM∥DE.
故②正确;
当CM⊥FM时,∠CMF=90°,
∵∠AMF=∠ABF=90°,
∴∠AMF+∠CMF=180°,即A,M,C在同一直线上,
∴∠MCF=45°,
∴∠MFC=90°﹣∠MCF=45°,
由翻折的性质可得:∠HBF=∠HMF=45°,BF=MF,
∴∠HMF=∠MFC,∠HBC=∠MFC,
∴BC∥MH,HB∥MF,
∴四边形BHMF是平行四边形,
∵BF=MF,
∴平行四边形BHMF是菱形,故③正确;
当点E运动到AB的中点,如图,
设正方形ABCD的边长为2a,则AE=BF=a,
在Rt△AED中,
,
∵∠AHD=∠FHB,∠ADH=∠FBH=45°,
∴△AHD∽△FHB,
∴,
∴.
∵∠AGE=∠ABF=90°,∠EAG=∠FAB,
∴△AGE∽△ABF,
∴,
∴,,
∴,.
∵∠BHF=∠DHA,
∴在Rt△DGH中,
,
故④错误;
由题意得:△ABF≌△AMF,
∴∠EAG=∠PAG,
在△EAG和PAG中,
,
∴△EAG≌PAG(ASA),
∴EG=PG,
∴EG=EP.
∵AD∥BC,
∴△AHD∽△FHB,
∴.
∵AD=AB,
∴.
∵∠AGE=∠ABF=90°,∠EAG=∠FAB,
∴△EAG∽△FAB,
∴,
∴,
∴EG•DH=AG•BH,
∴EP•DH=AG•BH,
∴EP•DH=2AG•BH,
故⑤正确.
综上分析可知,正确的是①②③⑤.
故选:B.
一十六.解直角三角形(共1小题)
20.(2021•黑龙江)如图,在△ABC中,∠ACB=90°,点D在AB的延长线上,连接CD,若AB=2BD,tan∠BCD=,则的值为( )
A.1 B.2 C. D.
【答案】B
【解答】解:过点D作DM⊥BC,交CB的延长线于点M,
∵∠ACB=∠DMB=90°,∠ABC=∠DBM,
∴△ABC∽△DBM,
∴==,
∵AB=2BD,
∴===,
在Rt△CDM中,
由于tan∠MCD==,设DM=2k,则CM=3k,
又∵==,
∴BC=2k,AC=4k,
∴==2,
故选:B.
一十七.解直角三角形的应用-坡度坡角问题(共1小题)
21.(2022•黑龙江)小明去爬山,在山脚看山顶角度为30°,小明在坡比为5:12的山坡上走1300米,此时小明看山顶的角度为60°,山高为( )米
A.600﹣250 B.600﹣250 C.350+350 D.500
【答案】B
【解答】解:设EF=5x米,
∵斜坡BE的坡度为5:12,
∴BF=12x米,
由勾股定理得:(5x)2+(12x)2=(1300)2,
解得:x=100,
则EF=500米,BF=1200米,
由题意可知,四边形DCFE为矩形,
∴DC=EF=500米,DE=CF,
在Rt△ADE中,tan∠AED=,
则DE==AD,
在Rt△ACB中,tan∠ABC=,
∴=,
解得:AD=600﹣750,
∴山高AC=AD+DC=600﹣750+500=(600﹣250)米,
故选:B.
一十八.由三视图判断几何体(共3小题)
22.(2023•黑龙江)一个由若干个大小相同的小正方体搭成的几何体,它的俯视图和左视图如图所示,那么组成该几何体所需小正方体的个数最少是( )
A.4 B.5 C.6 D.7
【答案】B
【解答】解:从俯视图可得最底层有4个小正方体,由左视图可得第二层最少有1个小正方体,最多有3个小正方体,
所以组成该几何体所需小正方体的个数最少是5个.
故选:B.
23.(2022•黑龙江)如图是一些完全相同的小正方体搭成的几何体的三视图.这个几何体只能是( )
A. B. C. D.
【答案】A
【解答】解:观察图象可知,选项A符合题意.
故选:A.
24.(2021•黑龙江)由若干个完全相同的小立方块搭成的几何体的左视图和俯视图如图所示,则搭成该几何体所用的小立方块的个数可能是( )
A.4个 B.5个 C.7个 D.8个
【答案】B
【解答】解:从左视图看第一列2个正方形,结合俯视图可知上面一层有1或2个正方体,左视图第二列1个正方形,结合俯视图可知下面一层有4个正方体,所以此几何体共有5或6个正方体.
故选:B.
一十九.频数与频率(共1小题)
25.(2022•黑龙江)王老师对本班40名学生的血型作了统计,列出如下的统计表,则本班A型血的人数是( )
组别
A型
B型
AB型
O型
频率
0.4
0.35
0.1
0.15
A.16人 B.14人 C.4人 D.6人
【答案】A
【解答】解:本班A型血的人数为:40×0.4=16.
故选:A.
二十.中位数(共1小题)
26.(2022•黑龙江)一组数据13,10,10,11,16的中位数和平均数分别是( )
A.11,13 B.11,12 C.13,12 D.10,12
【答案】B
【解答】解:把这组数据按从大到小的顺序排列是:10,10,11,13,16,
∴这组数据的中位数是:11,
平均数=(13+10+10+11+16)÷5=12.
故选:B.
二十一.众数(共2小题)
27.(2023•黑龙江)已知一组数据1,0,﹣3,5,x,2,﹣3的平均数是1,则这组数据的众数是( )
A.﹣3 B.5 C.﹣3和5 D.1和3
【答案】C
【解答】解:∵数据1,0,﹣3,5,x,2,﹣3的平均数是1,
∴1+0﹣3+5+x+2﹣3=7×1,
解得x=5,
则这组数据为1,0,﹣3,5,5,2,﹣3,
∴这组数据的众数为﹣3和5,
故选:C.
28.(2021•黑龙江)从小到大的一组数据﹣1,1,2,x,6,8的中位数为2,则这组数据的众数和平均数分别是( )
A.2,4 B.2,3 C.1,4 D.1,3
【答案】B
【解答】解:∵一组数据﹣1,1,2,x,6,8的中位数为2,
∴x=2×2﹣2=2,
2出现的次数最多,故这组数据的众数是2,
这组数据的平均数是(﹣1+1+2+2+6+8)÷6=3.
故选:B.
二十二.列表法与树状图法(共1小题)
29.(2022•黑龙江)袋子里有4个球,标有2,3,4,5,先抽取一个并记住,放回,然后再抽取一个,所抽取的两个球数字之和大于6的概率是( )
A. B. C. D.
【答案】C
【解答】解:画树状图得:
∵共有16种等可能的结果,抽取的两个球数字之和大于6的有10种情况,
∴抽取的两个球数字之和大于6的概率是:=.
故选:C.
二十三.排列与组合问题(共1小题)
30.(2021•黑龙江)大课间,12人跳绳队为尊重每个队员的意愿,准备把队员分成跳大绳组或跳小绳组,大绳组3人一组,小绳组2人一组,在全队同学能同时参加活动且符合小组规定人数的前提下,则不同的分组方法有( )
A.1种 B.2种 C.3种 D.4种
【答案】C
【解答】解:方法一:∵全队12人同时参加活动且符合小组规定的人数,且大绳组3人一组,小绳组2人一组,
∵12是偶数,2的倍数也是偶数,
又∵偶数+偶数=偶数,
∴大绳组人数必须为偶数,
即大绳组有0组、两组或四组三种分组情况;
方法二:设大绳组有x组,小绳组有y组,且x和y都是自然数,
由题知3x+2y=12,
∵x和y都是自然数,
∴或或,
即有3种分组情况,
故选:C.
河南省2021-2023三年中考数学真题分类汇编-01选择题知识点分类: 这是一份河南省2021-2023三年中考数学真题分类汇编-01选择题知识点分类,共25页。
陕西省2021-2023三年中考数学真题分类汇编-01选择题(基础题)知识点分类: 这是一份陕西省2021-2023三年中考数学真题分类汇编-01选择题(基础题)知识点分类,共18页。
青海省2021-2023三年中考数学真题分类汇编-01选择题知识点分类: 这是一份青海省2021-2023三年中考数学真题分类汇编-01选择题知识点分类,共19页。












