






高考数学一轮总复习课件第7章平面解析几何第1讲直线的倾斜角与斜率直线方程(含解析)
展开(1)定义:当直线 l 与 x 轴相交时,取 x 轴作为基准,x轴正向与直线 l 向上方向之间所成的角α叫做直线 l 的倾斜角.
(2)范围:直线 l 倾斜角α的取值范围是 0°≤α<180°.
(1)若直线 l 的倾斜角α≠90°,则斜率 k=tan α.
3.直线方程的五种形式
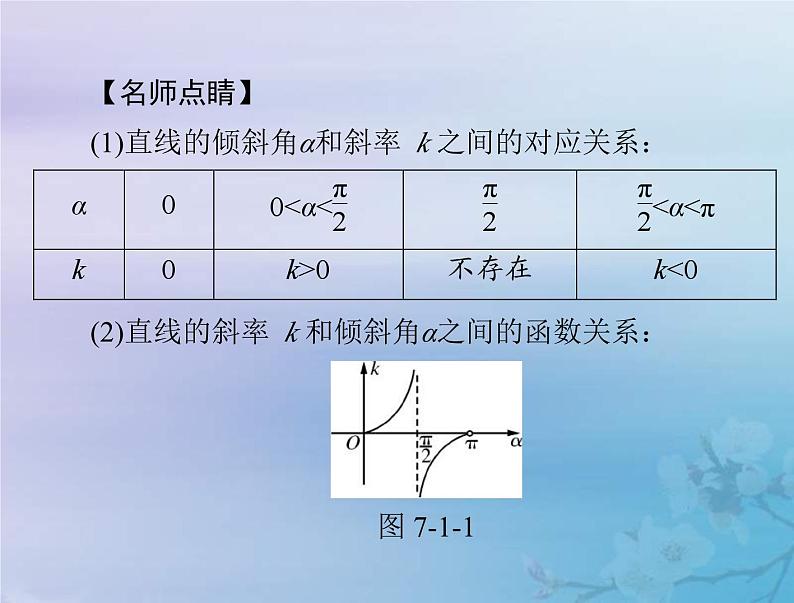
(1)直线的倾斜角α和斜率 k 之间的对应关系:
(2)直线的斜率 k 和倾斜角α之间的函数关系:
1.(多选题)下列说法错误的是(
C.直线 y=kx+b 与 y 轴的交点到原点的距离为 bD.平面内的所有直线的方程都可以用斜截式来表示答案:BCD
2.(教材改编题)经过两点 A(4,2y+1),B(2,-3)的直线
3.(教材改编题)过点 M(-3,5)且在两坐标轴上的截距
互为相反数的直线方程为(
A.x-y+8=0B.5x+3y=0C.x-y+8=0 或 5x+3y=0D.x+y-8=0 或 5x-3y=0答案:C
4.(2020 年全国Ⅲ)点(0,-1)到直线 y=k(x+1)距离的
[例 1](1)已知α∈R,则直线 xsin α-y-2 022=0 的倾
解析:因为直线的方程为 xsin α-y-2 022=0,所以直线的斜率为 k=sin α,所以-1≤k≤1,设直线的倾斜角为β,则有 k=tan β,所以-1≤tan β≤1,又因为 0≤β<π,
(2)(2021 年眉山期末)经过点 P(0,-1)作直线 l,若直线 l 与连接 A(1,-2),B(2,1)的线段总有公共点,则直线
l 的倾斜角的取值范围为(
A.0°≤α≤45°或135°≤α≤180°B.45°≤α≤135°C.45°<α<135°D.0°≤α≤45°或135°≤α<180°
解析:如图 7-1-2,图 7-1-2∵A(1,-2),B(2,1),P(0,-1),
则使直线 l 与线段 AB 有公共点的直线 l 的斜率的取值
∴倾斜角的取值范围为 0°≤α≤45°或 135°≤α<180°.
(1)由直线倾斜角的取值范围求斜率的取值范围或由斜率的取值范围求直线倾斜角的取值范围时,常借助正切函数 y=tan x 在[0,π)上的单调性求解,这里特别要注意,正切函数在[0,π)上并不是单调的.
(2)过一定点作直线与已知线段相交,求直线斜率的取
[例 2](2021 年寿光期中)求适合下列条件的直线方程:(1)经过点 A(2,-3),并且其倾斜角等于直线 x- y+1=0 的倾斜角的 2 倍的直线方程.(2)求经过点 A(-2,2)并且和两个坐标轴围成的三角形的面积是 1 的直线方程.
(1)在求直线方程时,应选择适当的形式,并注意各种
(2)对于点斜式、截距式方程使用时要注意分类讨论思想的运用(若采用点斜式,应先考虑斜率不存在的情况;若采用截距式,应先判断截距是否为零).
2.求过点 A(-5,2),且在 x 轴上的截距等于在 y 轴上的截距的 2 倍的直线方程.
[例 3]已知直线 l 过点 M(2,1),且分别与 x 轴的正半轴、y 轴的正半轴交于 A,B 两点,O 为原点,当△AOB 面积最小时,求直线 l 的方程.
(1)求解与直线方程有关的最值问题,先根据题意建立
目标函数,再利用基本不等式(或函数)求解最值.(2)求解直线方程与函数相结合的问题,一般是利用直线方程中 x,y 的关系,将问题转化为关于 x(或 y)的函数,借助函数的性质解决问题.
【变式训练】已知 0<k<4,直线 L:kx-2y-2k+8=0 和直线 M:2x+k2y-4k2-4=0与两坐标轴围成一个四边形,则这个
四边形面积最小时 k 值为(
解析:如图 D66 所示,直线 L:kx-2y-2k+8=0 即k(x-2)-2y+8=0,过定点 B(2,4),与 y 轴的交点 C(0,4-k),直线M:2x+k2y-4k2-4=0,即2x+k2(y-4)-4=0,过定点(2,4),与x 轴的交点A(2k2+2,0),由题意,
A.2x+y+2=0B.2x+y+2=0 或 2x+y-18=0C.2x-y-18=0D.2x-y+2=0 或 2x-y-18=0
抓住导数的几何意义及直线方程的求法是解决此类问
2.已知不全为零的实数 a,b,c 成等差数列,过点 A(1,2)作直线 l:ax+by+c=0 的垂线与直线 l 交于点 P,点 Q 在直线 3x-4y+12=0 上,则|PQ|的最小值是________.
高考数学一轮总复习课件第7章平面解析几何第7讲抛物线(含解析): 这是一份高考数学一轮总复习课件第7章平面解析几何第7讲抛物线(含解析),共48页。PPT课件主要包含了抛物线的定义,题组一,走出误区,定相切,答案1×,2×3×,题组二,走进教材,题组三,真题展现等内容,欢迎下载使用。
高考数学一轮总复习课件第7章平面解析几何第5讲椭圆(含解析): 这是一份高考数学一轮总复习课件第7章平面解析几何第5讲椭圆(含解析),共60页。PPT课件主要包含了椭圆的概念,题组一,走出误区,的轨迹是椭圆,答案1×,2×3√,题组二,走进教材,答案A,题组三等内容,欢迎下载使用。
高考数学一轮总复习课件第7章平面解析几何第3讲圆的方程(含解析): 这是一份高考数学一轮总复习课件第7章平面解析几何第3讲圆的方程(含解析),共42页。PPT课件主要包含了圆的定义与方程,点与圆的位置关系,名师点睛,题组一,走出误区,值可为,答案AB,题组二,走进教材,答案D等内容,欢迎下载使用。












