江苏省宜兴市树人中学教育集团2023-2024学年八年级上学期第一次（月考）调研数学试卷

树人教育集团2023～2024学年第一次调研测试八年级数学试卷

      考试时间：90分钟         满分：100分

一．选择题（共10题，每小题3分）

1．下列交通标志图案是轴对称图形的是  （    )

2．下列说法正确的是（　　）

A．形状相同的两个三角形全等          B．面积相等的两个三角形全等 

C．完全重合的两个三角形全等          D．全等三角形的周长和面积不相等

3.如果一个三角形是轴对称图形，那么这个三角形一定是（　　）

A．直角三角形 B．等腰三角形 C．锐角三角形 D．等边三角形

4．如下图所示，某同学把一块三角形的玻璃不小心打碎成了三块，现在要到玻璃店去配一块完全一样的玻璃，那么最省事的办法是带哪块去？  （     ）                           

A．①              B．②              C．③             D．①和②

5. △ABC的6个元素，如左图所示，下面甲、乙、丙三个三角形中和△ABC全等的是（　　）

A．只有乙 B．只有丙 C．甲和乙         D．乙和丙

6．若△ABC与△DEF全等，且∠A＝50°，∠B＝70°，则∠D的度数不可能是（　　）

A．80°        B．70°        C．60°        D．50°

        4              第7题               第8题                 第9题

7．如图，AB＝AC，需说明△ADC≌△AEB，可供添加的条件如下：①∠B＝∠C，②AD＝AE，

③∠ADC＝∠AEB，④DC＝BE，选择其中一个能使△ADC≌△AEB，则成立的个数是（　　）

A．1个            B．2个           C．3个           D．4个

8．如图，要测池塘两端A，B的距离，小明先在地上取一个可以直接到达A和B的点C，连接AC并延长到D，使CD＝CA；连接BC并延长到E，使CE＝CB，由△ABC和△DEC全等得到DE＝AB．那么判定其全等的依据是（　　）

A．SSS             B．SAS                 C．ASA               D．AAS

9．如图，AD是△ABC的角平分线，DE⊥AC，垂足为E，BF∥AC交ED的延长线于点F，若

BC恰好平分∠ABF，AE＝2BF．给出下列四个结论：①DE＝DF；②DB＝DC；③AD⊥BC；

④AC＝3BF．其中正确的结论为（　　）

A．①②③ B．①②④ C．②③④       D．①②③④

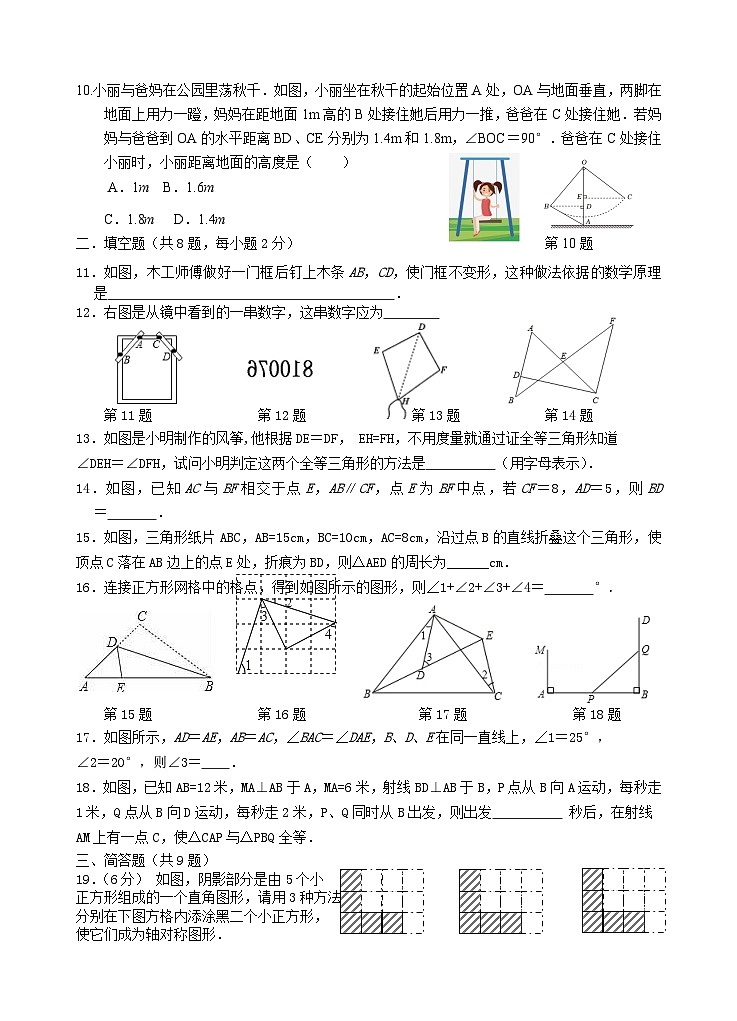
10.小丽与爸妈在公园里荡秋千．如图，小丽坐在秋千的起始位置A处，OA与地面垂直，两脚在地面上用力一蹬，妈妈在距地面1m高的B处接住她后用力一推，爸爸在C处接住她．若妈妈与爸爸到OA的水平距离BD、CE分别为1.4m和1.8m，∠BOC＝90°．爸爸在C处接住小丽时，小丽距离地面的高度是（　　）

​  A．1m  B．1.6m

C．1.8m   D．1.4m

二．填空题（共8题，每小题2分）                                   第10题

11．如图，木工师傅做好一门框后钉上木条AB，CD，使门框不变形，这种做法依据的数学原理是　                                     　．

12．右图是从镜中看到的一串数字，这串数字应为       

第11题               第12题               第13题            第14题

13．如图是小明制作的风筝,他根据DE＝DF， EH=FH，不用度量就通过证全等三角形知道

∠DEH＝∠DFH，试问小明判定这两个全等三角形的方法是          （用字母表示）．

14．如图，已知AC与BF相交于点E，AB∥CF，点E为BF中点，若CF＝8，AD＝5，则BD＝　   　．

15．如图，三角形纸片ABC，AB=15cm，BC=10cm，AC=8cm，沿过点B的直线折叠这个三角形，使顶点C落在AB边上的点E处，折痕为BD，则△AED的周长为______cm．

16．连接正方形网格中的格点，得到如图所示的图形，则∠1+∠2+∠3+∠4＝　   　°．

第15题               第16题                第17题               第18题

17．如图所示，AD＝AE，AB＝AC，∠BAC＝∠DAE，B、D、E在同一直线上，∠1＝25°，

∠2＝20°，则∠3＝　　．

18．如图，已知AB=12米，MA⊥AB于A，MA=6米，射线BD⊥AB于B，P点从B向A运动，每秒走

1米，Q点从B向D运动，每秒走2米，P、Q同时从B出发，则出发           秒后，在射线

AM上有一点C，使△CAP与△PBQ全等．

三、简答题（共9题）

19．（6分） 如图，阴影部分是由5个小

正方形组成的一个直角图形，请用3种方法

分别在下图方格内添涂黑二个小正方形，

使它们成为轴对称图形．

20.（6分）如图：AB=AD, ∠BAC=∠DAC，求证：△ABC≌△ADC   

21. （6分）已知：如图，∠1＝∠2，AD＝AB，∠AED＝∠C，求证：△ADE≌△ABC．

22. （6分）如图，已知：在△AFD和△CEB中，点A、E、F、C在同一直线上，AE＝CF，

∠D＝∠B，AD∥BC．求证：DF∥EB．

23. （6分）如图，在Rt△ABC中，∠C=90°，

（1）求作∠BAC的平分线，与BC交于点D（用尺规作图，保留作图痕迹，不写作法）。

（2）若CD=4，AB=15，求△ABD的面积。

24. （6分） 如图，点B、F、C、E在同一直线上，AC、DF相交于点G，AB⊥BE，垂足为B，DE⊥BE，垂足为E，且AC＝DF，BF＝CE．

（1）求证：△ABC≌△DEF；

（2）若∠A＝65°，求∠AGF的度数．

25. （8分）如图，DE⊥AB于E，DF⊥AC于F，若BD＝CD、BE＝CF，

（1）求证：AD平分∠BAC；

（2）已知AC＝20，BE＝4，求AB的长．

26.（10分） 如图，在△ABC中，∠BAD＝∠DAC，DF⊥AB，DM⊥AC，AF＝10cm，AC＝14cm，

动点E以2cm/s的速度从A点向F点运动，动点G以1cm/s的速度从C点向A点运动，当一个

点到达终点时，另一个点随之停止运动，设运动时间为t．

（1）求证：AF＝AM

（2）当t取何值时，△DFE与△DMG全等．

（3）求证：在运动过程中，不管t取何值，都有＝．