奥数六年级下册秋季课程 第12讲《追及问题》课件+教案

这是一份奥数六年级下册秋季课程 第12讲《追及问题》课件+教案，文件包含奥数六年级下册秋季课程第12讲《追及问题》课件pptx、奥数六年级下册秋季课程第12讲《追及问题》教案doc等2份课件配套教学资源，其中PPT共18页， 欢迎下载使用。

奥数六年级下册秋季课程
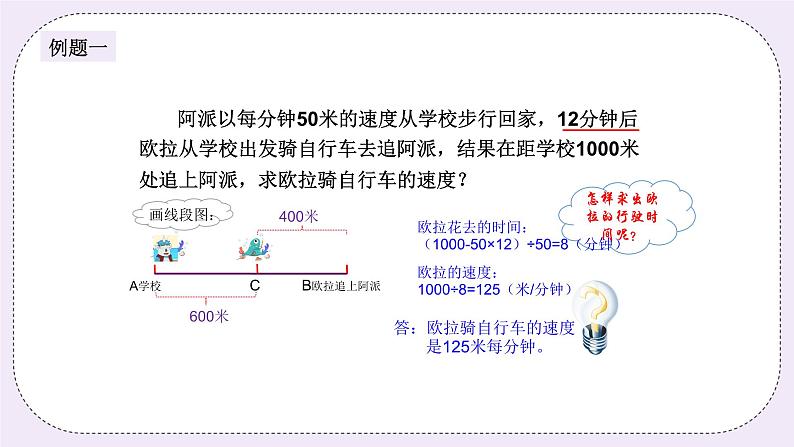
阿派以每分钟50米的速度从学校步行回家，12分钟后欧拉从学校出发骑自行车去追阿派，结果在距学校1000米处追上阿派，求欧拉骑自行车的速度？
怎样求出欧拉的行驶时间呢？
A学校 C B欧拉追上阿派
欧拉花去的时间：（1000-50×12）÷50=8（分钟）
欧拉的速度：1000÷8=125（米/分钟）
答：欧拉骑自行车的速度 是125米每分钟。
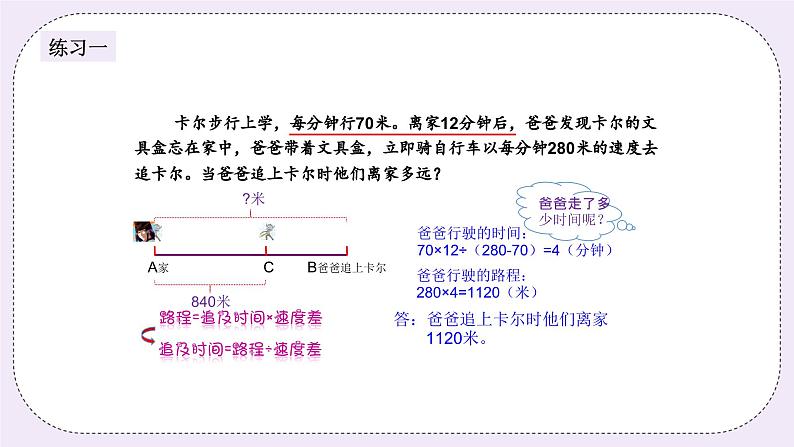
卡尔步行上学，每分钟行70米。离家12分钟后，爸爸发现卡尔的文具盒忘在家中，爸爸带着文具盒，立即骑自行车以每分钟280米的速度去追卡尔。当爸爸追上卡尔时他们离家多远？
路程=追及时间×速度差
A家 C B爸爸追上卡尔
追及时间=路程÷速度差
爸爸行驶的时间：70×12÷（280-70）=4（分钟）
爸爸行驶的路程：280×4=1120（米）
答：爸爸追上卡尔时他们离家 1120米。
在300米的环形跑道上，阿派和欧拉同时同地起跑，如果同向而跑2分30秒相遇，如果背向而跑则半分钟相遇，求两人的速度各是多少？
两者速度差：300÷150=2 （米/秒）
两者速度和：300÷30=10（米/秒）
大数=（10+2）÷2=6（米/秒）小数=（10-2）÷2=4（米/秒）
答：两人的速度各是6米每秒，4米每秒。
在400米的环形跑道上，甲、乙两人同时同地起跑，如果同向而行3分20秒相遇，如果背向而行40秒相遇，已知甲比乙快，求甲、乙的速度各是多少？
答：甲的速度是6米每秒，乙是4米每秒。
甲、乙速度差：400÷200=2（米/秒）
甲、乙速度和：400÷40=10（米/秒）
甲的速度：（10+2）÷2=6（米/秒）乙的速度：（10-2）÷2=4（米/秒）
1. 理清题意转换找出路程、追及时间、速度差中的其中两项。
2. 有相遇问题的追及问题，需要熟练运用和差公式解决问题。
甲、乙二人练习跑步，若甲让乙先跑10米，则甲跑5秒钟可追上乙；若乙比甲先跑2秒钟，则甲跑4秒钟能追上乙。问：两人每秒钟各跑多少米？
答：甲的速度是6米每秒，乙的速度是4米每秒。
甲 乙 追上
甲 乙 追上
速度差：10÷5=2（米/秒）
乙的速度：2×4÷2=4（米/秒）
甲的速度：4+2=6（米/秒）
甲、乙二人练习跑步，若甲让乙先跑15米，则甲跑5秒钟可追上乙；若乙比甲先跑3秒钟，则甲跑6秒钟能追上乙。问：两人每秒钟各跑多少米？
答：甲的速度是9米每秒，乙 的速度是6米每秒。
甲乙速度差：15÷5=3（米/秒）
乙的速度：6×3÷3=6（米/秒）
甲的速度：6+3=9（米/秒）
学校组织军训，甲、乙、丙三人步行从学校到军训驻地。甲、乙两人早晨7点一起从学校出发，甲每小时走6千米，乙每小时走5千米，丙上午9点才从学校出发，下午5点甲、丙同时到达军训驻地。问：丙在何时追上乙?
速度差=追及路程 ÷追及时间
丙的速度：6+2×6÷8=7.5（千米/小时）
乙丙追及时间：5×2÷（7.5-5）=4（小时）
9点过了4小时是下午1点。
答：丙在下午1点追上乙。
追及时间=追及路程 ÷速度差
甲乙丙三人都从A城到B城，甲乙两人早晨6点一起从A城出发，甲每小时走5千米，乙每小时走4千米，丙上午8点才从A城出发，下午6点甲、丙同时到达B城。问：丙在何时追上乙？
丙的速度：5+2×5÷10=6（千米/小时）
乙丙追及时间：2×4÷（6-4）=4（小时）
丙开始出发后过了4小时是12点。
答：丙在12点追上乙。
骑车人以每分钟300米的速度沿公共汽车路线前进，当他离始发站3000米时，一辆公共汽车从始发站出发，它的速度为每分钟700米，并且每行3分钟到达一站停车1分钟。问：公共汽车多长时间追上骑车人？
假设汽车一直行驶，速度为：700×3÷4=525（米/分钟）
“追及”时间：3000÷（525-300）=13余数75
13÷4=3余1，在11分钟停了1分钟
11分钟汽车行驶路程：9×700=12×525=6300（米）
11分钟骑车行驶路程：11×300=3300（米）
6300=3300+3000，最后一次停车刚好追上骑车人。
答：11分钟后公共汽车刚好追上骑车人。
米德骑车每分钟行200米，阿派步行每分钟80米。阿派出发3.6千米后米德骑车去追阿派，但米德每行5分钟就要停1分钟。米德追上阿派要多长时间？
假设米德骑车一直行驶，速度为：（200×5÷6）米/分钟
追及时间：3600÷（200×5÷6-80）≈41（分钟）行驶了41分钟开始休息了1分钟
米德41分钟行驶路程：42×200×5÷6=7000（米）阿派41分钟行驶路程：41×80=3280（米）
3280+3600=6880＜7000，所以在这次停车前已经追上了阿派。
最后停车时间在36分钟，36÷6×5×200=6000（米）阿派走了80×36=2880（米）
追及时间：（2880+3600-6000）÷（200-80）=4（分钟）
追上阿派需要36+4=40（分钟）
答：米德追上阿派要40分钟。
1. 通过转换等量关系（速度差不变），得出所求量。
2. 当出现走停情况时，运用假设法，分析最后次停车时间。