





奥数六年级上册 第12讲:圆柱的表面积 课件+教案
展开( 六年级 ) 备课教员:××× | |||
第十二讲 圆柱的表面积 | |||
一、教学目标: | 1. 掌握圆柱体侧面积和表面积的计算方法,能利用公式计算 圆柱的表面积,并能解决生活实际问题。
问题的能力。 3. 激发对数学的兴趣,在生活中发现数学。 | ||
二、教学重点: | 利用公式计算圆柱的表面积。 | ||
三、教学难点: | 圆柱表面积的推导,及分析生活中的圆柱表面积问题。 | ||
四、教学准备: | PPT、圆柱体模具 | ||
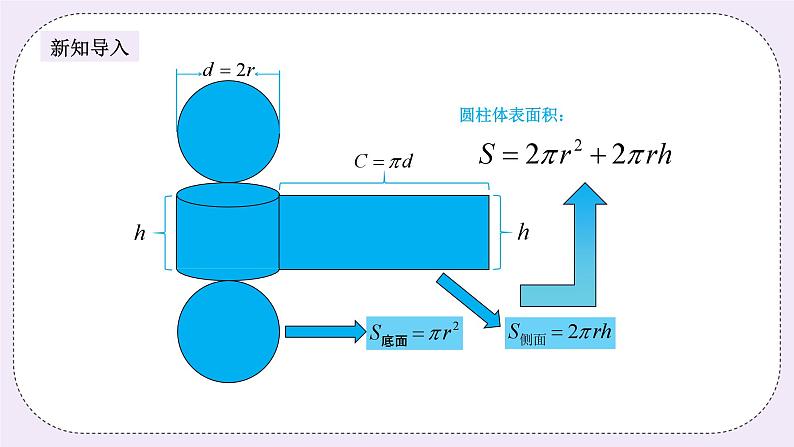
五、教学过程: 第一课时(50分钟) 一、导入(5分) 师:同学们,前两课我们学了很多平面图形的面积计算方法。之前我们也学过 长方体和正方体的表面积,你们还记得它们的表面积怎么求吗? 生:记得…… 师:嗯,很好,同学们掌握得不错。你们猜今天老师要带大家学习什么内容? 生:圆柱的表面积。 【板书课题:圆柱的表面积】 师:嗯,看来同学们都预习过了。老师手里有一个圆柱体,同学们告诉我,如 果要求圆柱的表面积,我们应该怎么算? 【邀请一个学生上台拿着圆柱体讲解】 生:两个圆,加一个曲面。 师:嗯,观察得很好。这两个圆我们叫作底面,这个曲面我们叫作侧面。圆的 面积同学们都会求,那么这个侧面呢? 生:…… 师:那老师提醒一下大家。其实同学们手中都有圆柱体,发现了没有? 生:没有。 师:同学们拿出一张草稿纸,像老师这样把它卷起来,如果我们把这两个面封 上,同学们发现了没有? 生:发现了。 师:所以圆柱体的侧面是什么形状? 生:长方形。 师:长方形的长是? 生:圆柱体的底面周长。 师:长方形的宽是? 生:圆柱体的高。 【结合课件,加深学生印象】 师:嗯,看起来大家好像已经会算了,那就来挑战一下吧,看同学们是不是真 的会了。 | |||
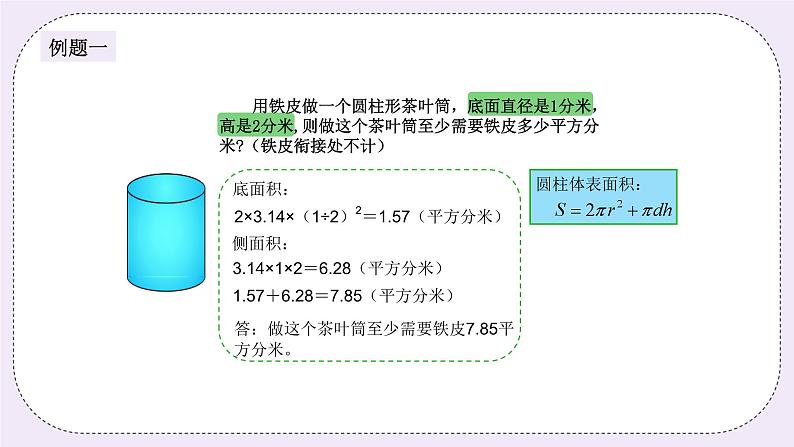
二、探索发现授课(40分) (一)例题1:(13分) 用铁皮做一个圆柱形茶叶筒,底面直径是1分米,高是2分米,则做这个茶叶筒至少需要铁皮多少平方分米?(铁皮衔接处不计) 师:要求这个茶叶筒需要多少铁皮,就是求? 生:表面积。 师:这个茶叶筒是什么形状? 生:圆柱。 师:嗯,圆柱的表面积是由哪两部分组成的? 生:两个底面和一个侧面。 师:嗯,底面比较好求,我们先来算底面的面积。 生:3.14×(1÷2)2。 师:但是圆柱是有两个底面的,所以,我们最后要? 生:乘2。 师:嗯,那侧面呢?我们先来回顾一下圆柱侧面的面积怎么求? 生:底面的周长乘高。 师:嗯,最后我们再把它们相加就可以了。 【教师先引导学生的解题思路,再结合课件详细讲解,加深学生印象】 板书: 3.14×(1÷2)2×2+3.14×1×2=7.85(平方分米) 答:做这个茶叶筒至少需要铁皮7.85平方分米。
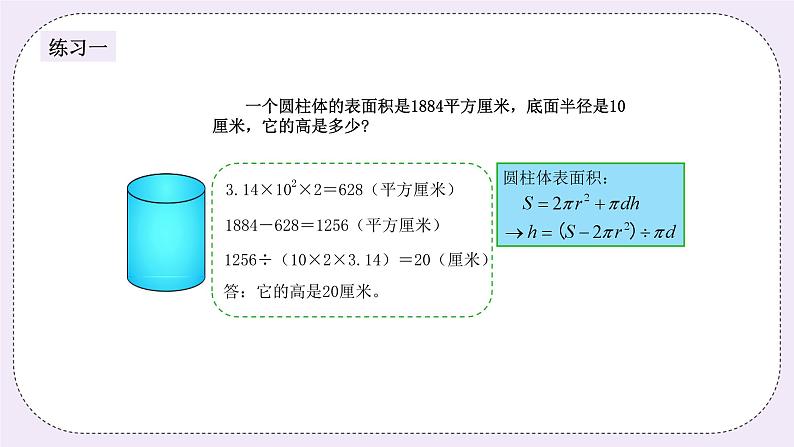
练习1:(6分) 一个圆柱体的表面积是1884平方厘米,底面半径是10厘米,它的高是多少? 分析: 已知圆柱的底面半径,可以求出两个底面积。圆柱的表面积减两个底面积就是圆柱的侧面积,利用侧面积公式的逆运算即可求出圆柱的高。 【教师邀请两个学生讲解自己的思路,由其他学生指出问题,教师重点指导不懂的学生】 板书: 3.14×102×2=628(平方厘米) 1884-628=1256(平方厘米) 1256÷(10×2×3.14)=20(厘米) 答:它的高是20厘米。
(二)例题2:(13分) 一个没有盖的圆柱形铁皮水桶,高是48厘米,底面直径是30厘米。做这个水桶至少要用铁皮多少平方厘米?(得数保留整百平方厘米) 师:做完例一和练习一以后,相信同学们对计算圆柱的表面积应该很自信了吧? 生:是。 师:好,那么同学们觉得例题二怎么做呢? 生:利用圆柱的表面积计算公式计算。 师:嗯,有没有同学发现什么问题? 生:这是一个没有盖的水桶。 师:没有盖,意味着什么? 生:圆柱的底面积只要算一个就可以了。 师:嗯,很好。所以在计算的时候其他都一样,只要底面积不乘二就好了。生 活中还有很多圆柱是没有盖的,或者没有底面积,大家在计算的时候一定 要注意了。 【教师先引导学生的解题思路,再结合课件详细讲解,加深学生印象】 板书: 3.14×(30÷2)2+3.14×30×48≈5200(平方厘米) 答:做这个水桶至少要用铁皮5200平方厘米。
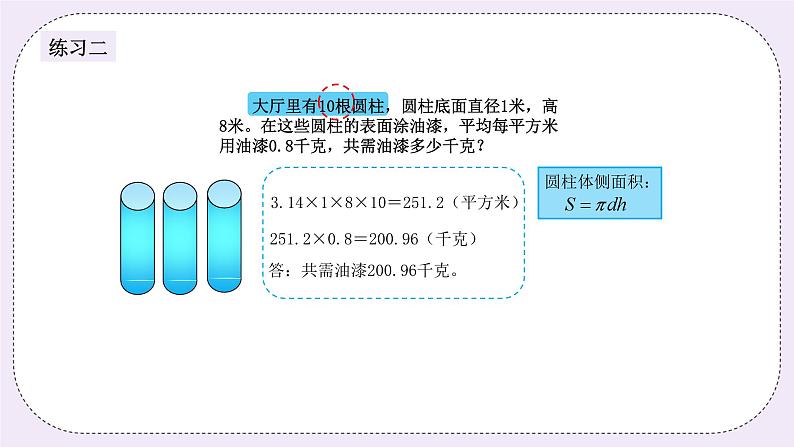
练习2:(8分) 大厅里有10根圆柱,圆柱底面直径1米,高8米。在这些圆柱的表面涂油漆,平均每平方米用油漆0.8千克,共需油漆多少千克? 分析: 大厅的圆柱是嵌入在天花板和地板中的,所以没有底面积,在涂油漆的时候只需要计算圆柱的侧面积即可。 【教师邀请两个学生讲解自己的思路,由其他学生指出问题,教师重点指导不懂的学生】 板书: 3.14×1×8×10×0.8=200.96(千克) 答:共需油漆200.96千克。
三、小结:(5分) 圆柱的一个底面积: 圆柱的侧面积: 圆柱的表面积: 计算表面积的时候要注意实际情况。 | |||
第二课时(50分) 一、复习导入(5分) 师:同学们,上节课我们学习了什么内容? 生:圆柱的表面积。 师:那在我们的生活中有哪些圆柱体,我们一起来找一找,3人一组(根据实际 情况分组),看哪个小组找得多。限时2分钟,现在开始。 生:…… 师:看来同学们都很会观察生活,接下来我们一起进入今天的课堂。相信同学 们学完今天的内容,都会变成计算圆柱表面积的高手。 (出示PPT) | |||
二、探索发现授课(40分) (一)例题3:(13分) 把一根直径是20厘米,长是2米的圆柱形木材锯成同样的3段,表面积增加了多少平方厘米? 师:如果我们有一根圆柱体,要把它切成平均的两份,可以怎么切? 生:沿着横截面切开。 生:沿着底面直径切开。 生:…… 师:同学们说得很好。那么这道题是怎么切的呢? 生:沿着横截面切。 师:沿着横截面切开可以得到什么? 生:两个新的圆柱。 师:表面积怎么计算呢? 生:…… 师:那和原来的表面积相比较呢? 生:增加了两个底面积。 师:这道题是把圆柱切成了3段,增加了几个底面积。 生:4个。 师:很好,大家再跟着老师一起来做一遍。 【教师先引导学生的解题思路,再结合课件详细讲解,加深学生印象】 板书: 3.14×(20÷2)2×4=1256(平方厘米) 答:表面积增加了1256平方厘米。
练习3:(7分) 把一根长1.2米的圆柱形木材锯成3段,表面积增加了50.24平方厘米,它没锯之前的表面积是多少? 分析: 切成3段,增加的表面积是4个底面积。已知增加的表面积可以求出原来的底面积和底面半径。 【教师邀请两个学生讲解自己的思路,由其他学生指出问题,教师重点指导不懂的学生】 板书: 50.24÷4=12.56(平方厘米) 12.56÷3.14=4(厘米) 底面半径是2厘米,1.2米=120厘米 12.56×2+3.14×2×2×120=1532.32(平方厘米) 答:它没锯之前的表面积是1532.32平方厘米。
(二)例题4:(13分) 一圆柱底面直径是4米,高是6米,沿着底面直径把圆柱切成两半,求表面积增加了多少? 师:上一题是沿着横截面切开,我们一起看一下这道题,有什么不同? 生:这道题是沿着底面直径切开。 师:沿着底面直径切成两半,截面是什么图形呢? 生:是两个长方形。 师:嗯,长方形的面积怎么求? 生:长乘宽。 师:长是什么? 生:高。 师:宽呢? 生:底面直径。 师:所以增加的表面积好求吗? 生:好求。 师:先跟着老师来做一遍。 【教师先引导学生的解题思路,再结合课件详细讲解,加深学生印象】 板书: 6×4×2=48(平方米) 答:表面积增加了48平方米。
练习4:(7分) 把一个圆柱体沿底面直径切开,表面积增加了24平方厘米,已知这个圆柱体的高是3厘米,求原来这个圆柱表面积是多少? 分析: 表面积增加了 24平方厘米,增加的一个面的面积是12平方厘米。已知高是3厘米,可以求出底面直径。再利用圆柱表面积公式求其原来的表面积。 【教师邀请两个学生讲解自己的思路,由其他学生指出问题,教师重点指导不懂的学生】 板书: 底面半径:24÷2÷3÷2=2(厘米) 3.14×22×2+3.14×2×2×3=62.8(平方厘米) 答:原来这个圆柱表面积是62.8平方厘米。
(三)例题5(选讲): 用铁皮做一个如右图所示的空心管(单位:厘米),需用铁皮多少平方厘米?
师:同学们已经学过求组合图形的面积,我们在做题的时候有哪些技巧? 生:填补、平移、拆分…… 师:这道题可以用这些技巧吗? 生:可以。 师:怎么来做? 生:分成上下两部分。 师:嗯,下面部分就是? 生:圆柱。 师:是圆柱,但是这个圆柱是? 生:空心的。 师:空心的,我们计算的时候只需要计算? 生:侧面积。 师:嗯,很好。那上面部分呢? 生:圆柱的一半。 师:同学们真厉害。我们一起来做一下。 【教师先引导学生的解题思路,再结合课件详细讲解,加深学生印象】 板书: 上半部分:3.14×6×(12-8)÷2=37.68(平方厘米) 下半部分:3.14×6×8=150.72(平方厘米) 37.68+150.72=188.4(平方厘米) 答:需用铁皮188.4平方厘米。
练习5: 将高是0.8米,底面半径分别为1.5米、1米和0.5米的三个圆柱组成一个物体,这个物体的表面积是多少? 分析: 可以分成两部分来计算,一部分是三个圆柱的侧面积,另一部分是上下两个面:下面就是大圆柱一个底面积,上面我们可以从上往下看,发现也是一个大圆柱的底面积。求和即可计算出其表面积。 【教师邀请两个学生讲解自己的思路,由其他学生指出问题,教师重点指导不懂的学生】 板书: 三个侧面积的和: 3.14×(1.5×2+1×2+0.5×2)×0.8=15.072(平方米) 上下面积的和: 3.14×1.52×2=14.13(平方米) 15.072+14.13=29.202(平方米) 答:这个物体的表面积是29.202平方米。
三、总结:(5分) 圆柱的侧面积: 圆柱的表面积: 沿圆柱横截面切成两段,增加的表面积是两个底面积: 沿圆柱底面直径切成两部分,增加的表面积是两个长方形: 四、随堂练习:
板书: 3.14×2×2×6=75.36(平方厘米) 答:它的侧面积是75.36平方厘米。
在池的一周及池底抹上水泥,抹水泥的面积是多少? 板书: 3.14×(10÷2)2=78.5(平方米) 3.14×10×2+78.5=141.3(平方米) 答:这个蓄水池的占地面积是78.5平方米,抹水泥的面积是141.3平方米。
3. 为了建筑的需要,现将2米长的圆柱形木料截成2段。已知木料的横截面直 径是6厘米,那么表面积比原来增加了多少平方厘米? 板书: 3.14×(6÷2)2×2=56.52(平方厘米) 答:那么表面积比原来增加了56.52平方厘米。
增加多少? 板书: 8×3×2=48(平方米) 答:表面积增加48平方米。
2厘米,求这个几何体的表面积是多少平方厘米?
板书: 3.14×22××2+3.14×2×2×4×+2×2×4=72.52(平方厘米) 答:这个几何体的表面积是72.52平方厘米。
| |||
家庭作业 | 线上作业:第12讲 | ||
主管评价 |
| ||
主管评分 |
| ||
课后反思 (不少于60字) | 整体效果 |
| |
设计不足之处 |
| ||
设计优秀之处 |
| ||
奥数四年级上册 第12讲:统计 课件+教案: 这是一份奥数四年级上册 第12讲:统计 课件+教案,文件包含奥数四年级上册第12讲统计课件pptx、奥数四年级上册第12讲统计教案doc等2份课件配套教学资源,其中PPT共27页, 欢迎下载使用。
奥数六年级上册 第15讲:抽屉原理 课件+教案: 这是一份奥数六年级上册 第15讲:抽屉原理 课件+教案,文件包含奥数六年级上册第15讲抽屉原理课件pptx、奥数六年级上册第15讲抽屉原理教案doc等2份课件配套教学资源,其中PPT共15页, 欢迎下载使用。
奥数六年级上册 第14讲:统计 课件+教案: 这是一份奥数六年级上册 第14讲:统计 课件+教案,文件包含奥数六年级上册第14讲统计课件pptx、奥数六年级上册第14讲统计教案doc等2份课件配套教学资源,其中PPT共17页, 欢迎下载使用。













