






2024届高考数学一轮复习(新教材人教A版强基版)第二章函数必刷小题3基本初等函数课件
展开一、单项选择题1.函数f(x)= +lg(3-x)的定义域为A.[1,3) B.(1,3)C.(-∞,1)∪[3,+∞) D.(-∞,1]∪(3,+∞)
f(f(1))=f(lg 1)=f(0)=100=1.
3.函数y=2+lg2(x2+3)(x≥1)的值域为A.(2,+∞) B.(-∞,2)C.[4,+∞) D.[3,+∞)
令t=x2+3≥4,因为y=2+lg2t在[4,+∞)上单调递增,所以y≥2+lg24=4,所以y=2+lg2(x2+3)(x≥1)的值域为 [4,+∞).
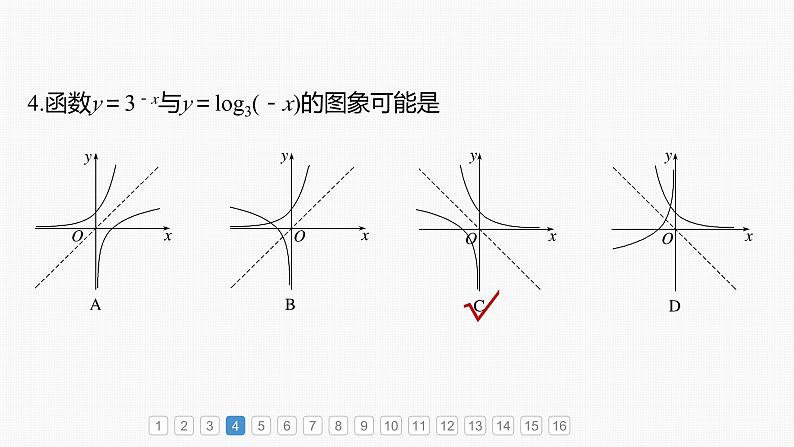
4.函数y=3-x与y=lg3(-x)的图象可能是
函数y=3-x= 为R上的减函数,排除A,B选项,函数y=lg3(-x)的定义域为(-∞,0),内层函数u=-x为减函数,外层函数y=lg3u为增函数,故函数y=lg3(-x)为(-∞,0)上的减函数,排除D选项.
A.a
依题意得f(0)=0,f(-x)=-f(x),
8.已知函数f(x)=lg2(4x+1)+ax是偶函数,函数g(x)=22x+2-2x+m·2f(x)的最小值为-3,则实数m的值为
因为函数f(x)=lg2(4x+1)+ax是偶函数,所以f(-1)=f(1),解得a=-1,所以f(x)=lg2(4x+1)-x,
故函数g(x)=22x+2-2x+m(2x+2-x)的最小值为-3.令2x+2-x=t,则t≥2,
故函数g(x)=22x+2-2x+m(2x+2-x)的最小值为-3,等价于h(t)=t2+mt-2(t≥2)的最小值为-3,
二、多项选择题9.已知实数a,b,c满足a>1>b>c>0,则下列说法正确的是A.aa>bb B.lgca
∴aa>ab>bb, > ,故A选项正确,D选项不正确;
又lgac
所以定义域为(-1,1),故A正确;
所以f(x)的图象关于原点对称,即f(x)在定义域上为奇函数,故B错误,C正确;
又y=lg x在(0,+∞)上单调递增,
11.已知函数f(x)=ax2-2ax+4(a>0),若x1
函数f(x)=ax2-2ax+4(a>0),二次函数的图象开口向上,对称轴为直线x=1,当x1+x2=2时,x1与x2的中点为1.∴f(x1)=f(x2),选项B正确;当x1+x2>2时,x1与x2的中点大于1,又x1
12.已知2a+a=lg2b+b=lg3c+c,则下列关系可能成立的是A.a
在同一坐标系中画出函数y=2x,y=lg2x,y=lg3x和y=-x+k的图象,如图,观察图象得,当k<1时,a
f(x)=ln x(答案不唯一)
因为y=ln x的定义域为(0,+∞)且在定义域上单调递增,所以依题意f(x)的一个解析式可以为f(x)=ln x.
15.若函数f(x)=a·bx+c在区间[0,+∞)上的值域是[-2,1),则ac=________.
因为x∈[0,+∞),f(x)=a·bx+c∈[-2,1),所以0
2024届高考数学一轮复习(新教材人教A版强基版)第七章立体几何与空间向量必刷小题13立体几何课件: 这是一份2024届高考数学一轮复习(新教材人教A版强基版)第七章立体几何与空间向量必刷小题13立体几何课件,共37页。PPT课件主要包含了填空题等内容,欢迎下载使用。
2024届高考数学一轮复习(新教材人教A版强基版)第六章数列必刷小题11数列课件: 这是一份2024届高考数学一轮复习(新教材人教A版强基版)第六章数列必刷小题11数列课件,共30页。PPT课件主要包含了单项选择题,故k3=09,nn+1等内容,欢迎下载使用。
2024届高考数学一轮复习(新教材人教A版强基版)第四章三角函数与解三角形必刷小题7三角函数课件: 这是一份2024届高考数学一轮复习(新教材人教A版强基版)第四章三角函数与解三角形必刷小题7三角函数课件,共33页。PPT课件主要包含了单项选择题,k∈Z的一个值即可等内容,欢迎下载使用。













