

2022-2023学年四川省遂宁市高二下学期期末数学(理)试题含答案
展开2022-2023学年四川省遂宁市高二下学期期末数学(理)试题
一、单选题
1.设是虚数单位,若复数,则的共轭复数为( )
A. B. C. D.
【答案】A
【分析】由复数的乘法运算以及共轭复数的定义即可求解.
【详解】由得,所以的共轭复数为,
故选:A
2.命题“,”的否定为( )
A., B.,
C., D.,
【答案】C
【分析】根据全称命题的否定为特称命题判断即可.
【详解】根据全称命题的否定可得,命题“,”的否定为
“,”.
故选:C
3.“”是“”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
【答案】B
【分析】根据充分、必要条件的知识确定正确答案.
【详解】,
所以,
所以“”是“”的必要不充分条件.
故选:B
4.设函数f(x)在定义域内可导,其图象如图所示,则导函数f′(x)的图象可能是( )
A. B.
C. D.
【答案】B
【分析】根据函数图象得出单调性,然后判断导函数的正负即可选出答案.
【详解】由函数的图象,知当时,是单调递减的,所以;
当时,先减少,后增加,最后减少,所以先负后正,最后为负.
故选:B.
【点睛】本题考查原函数的单调性与导函数的正负的关系.属于基础题.
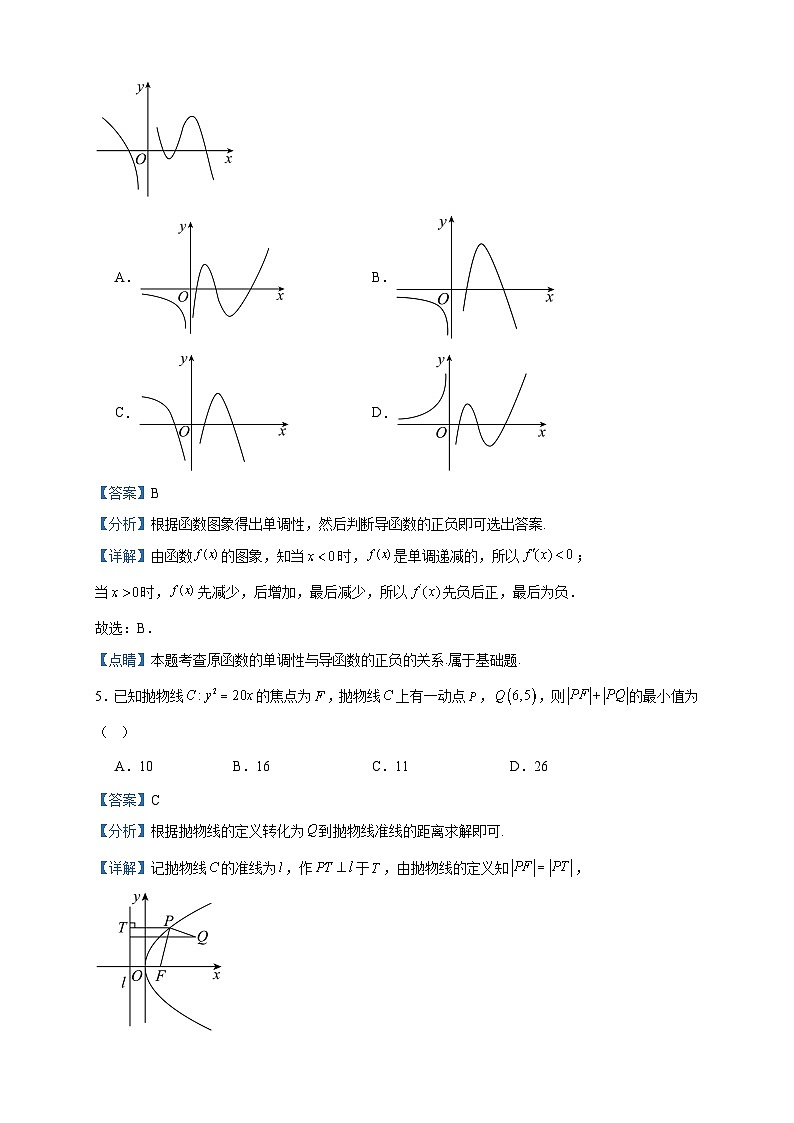
5.已知抛物线的焦点为,抛物线上有一动点,,则的最小值为( )
A.10 B.16 C.11 D.26
【答案】C
【分析】根据抛物线的定义转化为到抛物线准线的距离求解即可.
【详解】记抛物线的准线为,作于,由抛物线的定义知,
所以,当,,三点共线时,有最小值,最小值为.
故选:C
6.“燃脂单车”运动是一种在音乐的烘托下,运动者根据训练者的指引有节奏的踩踏单车,进而达到燃脂目的的运动,由于其操作简单,燃脂性强,受到广大健身爱好者的喜爱.已知某一单车爱好者的骑行速度v(单位:km/h)随时间t(单位:h)变换的函数关系为,,则该单车爱好者骑行速度的最大值为( )
A. B. C. D.
【答案】C
【分析】求出函数的导函数,即可得到函数的单调区间,求出函数的最小值,即可得解.
【详解】因为,,
所以,所以时,当时,
所以在上单调递增,在上单调递减,
所以.
故选:C
7.短道速滑队6名队员(含赛前系列赛积分最靠前的甲乙丙三名队员在内)进行冬奥会选拔,记“甲得第一名”为p,“乙得第二名”为q,“丙得第三名”为r,若是真命题,是假命题,是真命题,则选拔赛的结果为( )
A.甲得第一名,乙得第二名,丙得第三名 B.甲得第二名,乙得第一名,丙得第三名
C.甲得第一名,乙得第三名,丙得第二名 D.甲得第一名,乙没得第二名,丙得第三名
【答案】D
【分析】根据或且非命题真假判断即可.
【详解】若是真命题,是假命题,则p和q一真一假;
若是真命题,则q是假命题,r是真命题;
综上可知,p真q假r真,故“甲得第一名、乙没得第二名、丙得第三名”.
故选:D.
8.要排出某班一天中语文、数学、政治、英语、体育、艺术6堂课的课程表,要求数学排在上午(前4节),体育课排在下午(后2节),不同排法种数是( )
A.720 B.192 C.180 D.144
【答案】B
【分析】根据题意,先排数学与体育,再排其余4节,然后由乘法原理即可得到结果.
【详解】由题意可得,要求数学课排在上午(前4节),体育课排在下午(后2节),有种,再排其余4节,有种,再根据乘法原理,共有种方法.
故选:B
9.已知圆,若双曲线的一条渐近线与圆C相切,则( )
A. B. C. D.8
【答案】C
【分析】求出圆心和半径,及双曲线的渐近线,由相切关系列出方程,求出答案.
【详解】变形为,故圆心为,半径为1,
的渐近线方程为,
不妨取,由点到直线距离公式可得,解得,负值舍去.
故选:C
10.若函数的最小值是,则实数m的取值范围是( )
A. B. C. D.
【答案】B
【分析】先求时函数的最小值,再根据函数的最小值,得时,,求出m的取值范围.
【详解】当时,,,
,,单调递减,
,,单调递增,,
因为的最小值为,所以当时,,
当时,.
①若,在上单调递减,
,,得;
②若,在上单调递减,在上单调递增,,舍去.
综上.
故选:B.
11.已知,则( )
A. B.
C. D.
【答案】D
【分析】构造函数,利用不等式的性质以及导数求解单调性即可两两比较求解.
【详解】令,
由于,
因此,
故,
令,
故在单调递增,,
即,
所以,因此,
故选:D
12.已知椭圆C:的左、右焦点分别为,,点M是椭圆C上任意一点,且的取值范围为.当点M不在x轴上时,设的内切圆半径为m,外接圆半径为n,则mn的最大值为( ).
A. B. C. D.1
【答案】C
【分析】由的取值范围为可求出,由正弦定理可得,再由焦点三角形的等面积法可得,所以,求出即可得出答案.
【详解】,
,所以,
所以,解得:,
设,
由正弦定理可得:,
,
可得:,
又因为,
设内切圆的圆心为A,所以,
所以,所以,
又因为当在短轴的端点时,最大,此时,,
,所以,
故当时,mn取得最大值为.
故选:C.
二、填空题
13.的展开式中的系数为 .
【答案】40
【分析】根据二项式展开式的通项公式,直接计算即可得到结果.
【详解】展开式的通项公式为,
令,则,所以的系数为.
故答案为:40.
14.已知方程表示椭圆,则实数k的取值范围是 .
【答案】且
【分析】根据方程表示椭圆有,即可得范围.
【详解】由方程表示椭圆,则,可得且.
故答案为:且
15.设双曲线的左、右焦点分别为,,为双曲线右支上一点,且,则的大小为 .
【答案】/
【分析】根据双曲线方程求出、、,再由双曲线的定义求出、,最后由余弦定理计算可得.
【详解】因为双曲线,则,,所以,
因为为双曲线右支上一点,所以,又,
所以,,,
由余弦定理,
即,解得,又,
所以.
故答案为:
16.已知函数在处的切线斜率为,,若在上恒成立,则能取到的最大正整数为
【答案】3
【分析】根据切线斜率可得,进而分离参数将问题转化为,构造函数,利用导数求解单调性,即可求解.
【详解】,,
由得,
故,
记,
由于,所以,有均为的单调递增函数,
所以为递增函数,,
故存在唯一的,使得,即,
故当因此单调递减,单调递增,
故,
由于,对勾函数在单调递减,故,所以,
所以能取到的最大正整数为3,
故答案为:3
【点睛】对于利用导数研究函数的综合问题的求解策略:
1、通常要构造新函数,利用导数研究函数的单调性,求出最值,从而求出参数的取值范围;
2、利用可分离变量,构造新函数,直接把问题转化为函数的最值问题.
3、根据恒成立或有解求解参数的取值时,一般涉及分离参数法,但压轴试题中很少碰到分离参数后构造的新函数能直接求出最值点的情况,进行求解,若参变分离不易求解问题,就要考虑利用分类讨论法和放缩法,注意恒成立与存在性问题的区别.
三、解答题
17.分别求适合下列条件的方程:
(1)长轴长为10,焦距为4的椭圆标准方程;
(2)经过点的抛物线的标准方程.
【答案】(1)或
(2)或
【分析】(1)根据长轴和焦距的定义求出a、c,进而求出b,即可求解;
(2)设抛物线方程为或,将点P坐标代入,即可求解.
【详解】(1)设椭圆的长轴长为,焦距为
由条件可得.所以.
所以,
当椭圆的焦点在轴上时,标准方程为;
当椭圆的焦点在轴上时,标准方程为.
(2)当抛物线的焦点在轴上时,可设所求抛物线的标准方程为,
将点的坐标代入抛物线的标准方程得,
此时,所求抛物线的标准方程为;
当抛物线的焦点在轴上时,可设所求抛物线的标准方程为,
将点的坐标代入抛物线的标准方程得,解得,
此时,所求抛物线的标准方程为.
综上所述,所求抛物线的标准方程为或.
18.已知函数的图象过点,且在点P处的切线恰好与直线垂直.
(1)求函数的解析式;
(2)若函数在区间上单调递增,求实数m的取值范围.
【答案】(1)
(2)或
【分析】(1)将点坐标代入函数解析式得到关于的方程,再根据函数在切点处的导数等于切线的斜率再建立关于的另一个方程,即可求出,即可确定函数的解析式; (2)求出函数的单调区间,利用可求解.
【详解】(1)因为函数的图象过点,所以,
又因为,且点P处的切线恰好与直线垂直,
所以,
由解得,所以.
(2)由(1)知,
令,即,解得或,
令,即,解得,
所以在单调递增,单调递减,
单调递增,
根据函数在区间上单调递增,
则有或,解得或.
19.党的二十大报告提出:“必须坚持科技是第一生产力、人才是第一资源、创新是第一动力,深入实施科教兴国战略、人才强国战略、创新驱动发展战略,开辟发展新领域新赛道,不断塑造发展新动能新优势.”某数字化公司为加快推进企业数字化进程,决定对其核心系统DAP,采取逐年增加研发人员的办法以提升企业整体研发和创新能力.现对2018~2022年的研发人数作了相关统计(年份代码1~5分别对应2018~2022年)如下折线图:
(1)根据折线统计图中数据,计算该公司研发人数与年份代码的相关系数,并由此判断其相关性的强弱;
(2)试求出关于的线性回归方程,并预测2023年该公司的研发人数(结果取整数).
参考数据:当认为两个变量间的相关性较强
参考公式相关系数,
回归方程中的斜率和截距的最小二乘法估计公式分别为,.
【答案】(1)相关系数为0.988,相关变量有较强的相关性
(2),540人
【分析】(1)将数据代入公式计算即可求解;
(2)结合(1)和题中的数据,代入公式计算即可求解.
【详解】(1)由题知
因为,所以认为相关变量有较强的相关性.
(2)由(1)得
回归方程为
当时,即2023年该公司投入研发人数约540人.
20.为提高学生的数学应用能力和创造力,学校打算开设“数学建模”选修课,为了解学生对“数学建模”的兴趣度是否与性别有关,学校随机抽取该校30名高中学生进行问卷调查,其中认为感兴趣的人数占70%.
(1)根据所给数据,完成下面的列联表,并根据列联表判断是否有85%的把握认为学生对“数学建模”选修课的兴趣度与性别有关?
| 感兴趣 | 不感兴趣 | 合计 |
男生 | 12 |
|
|
女生 |
| 5 |
|
合计 |
|
| 30 |
(2)若感兴趣的女生中恰有4名是高三学生,现从感兴趣的女生中随机选出3名进行二次访谈,记选出高三女生的人数为X,求X的分布列与数学期望.
附:,其中.
0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 | |
2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【答案】(1)表格见解析,没有85%的把握;
(2)分布列见解析,.
【分析】(1)由题可得列联表,根据列联表可得进而即得;
(2)由题可得X的取值,然后利用古典概型概率公式求概率,进而可得分布列,再利用期望公式即得.
【详解】(1)列联表如下:
| 感兴趣 | 不感兴趣 | 合计 |
男生 | 12 | 4 | 16 |
女生 | 9 | 5 | 14 |
合计 | 21 | 9 | 30 |
,
所以没有85%的把握认为学生对“数学建模”选修课的兴趣度与性别有关;
(2)由题意可知X的取值可能为0,1,2,3,
则,
,
,
,
故X的分布列为
X | 0 | 1 | 2 | 3 |
P |
.
21.已知椭圆与双曲线有相同的焦点,为椭圆上一点,面积最大值为.
(1)求椭圆的方程;
(2)直线与椭圆相交于两点,若轴,垂足为.求证:直线的斜率;
(3)为椭圆的右顶点,若过点且斜率不为0的直线交椭圆于两点,为坐标原点.问:轴上是否存在定点,使得恒成立.若存在,请求出点的坐标;若不存在,请说明理由.
【答案】(1)
(2)证明见解析
(3)存在
【分析】(1)先求得,然后求得,从而求得椭圆的方程.
(2)设,求得的坐标,进而求得直线的斜率.
(3)设直线l为且,并与椭圆方程联立,化简写出判别式和根与系数关系,由列方程,化简求得的坐标.
【详解】(1)双曲线的焦点坐标为,所以椭圆的焦点坐标为,则,
又椭圆中,由于,
所以面积最大值,故,则,
所以椭圆的方程为:.
(2)设,由于直线过原点,则,.
所以直线的斜率.
(3)由题设,可设直线l为且,联立椭圆方程,
整理得:,
则,
所以,即且,
所以,,
若存在使恒成立,则,
由椭圆对称性,不妨令在轴上方且,显然,
所以,即,
所以,
即,
综上,,
所以,存在使恒成立.
22.已知函数(是自然对数的底数).
(1)讨论函数的单调性;
(2)若有两个零点分别为.
①求实数的取值范围;
②求证:.
【答案】(1)答案见解析
(2)①;②证明见解析
【分析】(1)根据题意,求导即可得到结果;
(2)①根据题意,将问题转化为有两个零点,然后利用导数,分类讨论即可得到的取值范围;
②根据题意,将问题转化为,再由①中的结论,即只需证,然后构造函数求导即可得到证明.
【详解】(1)由题意可得,
①当时,在上递增;
②当时,在上递减,在上递增.
(2)①等价于有两个零点,
令,则,在时恒成立,所以在时单调递增,
所以有两个零点,等价于有两个零点.
因为 ,所以当时,,单调递增,不可能有两个零点;
当时,令,得,单调递增,令,得,单调递减,所以,
若,得,此时恒成立,没有零点;
若,得,此时有一个零点;
若,得,因为,,,
所以在,上各存在一个零点,符合题意,
综上,a的取值范围为.
②要证即证:,
即证,由(2)中①知,,所以只需证.
因为,,所以,,
所以 ,只需证.
设,令, 则,所以只需证 , 即证 ,
令,,则 ,,
即当时, 成立.
所以,即.
【点睛】关键点睛:本题主要考查了利用导数研究函数零点问题与利用导数证明不等式问题,难度较大,解答本题的关键在于根据题意来构造函数,然后通过导数研究函数的性质得到证明.
四川省遂宁市2019-2020学年高二下学期期末考试 数学(理)试卷: 这是一份四川省遂宁市2019-2020学年高二下学期期末考试 数学(理)试卷,共12页。试卷主要包含了考试结束后,将答题卡收回等内容,欢迎下载使用。
2022-2023学年四川省遂宁市高二下学期期末监测数学试题word版含答案: 这是一份2022-2023学年四川省遂宁市高二下学期期末监测数学试题word版含答案,文件包含高二数学理科答案doc、高二数学文科答案doc、高二数学文科doc、高二数学理科doc等4份试卷配套教学资源,其中试卷共25页, 欢迎下载使用。
2022-2023学年四川省遂宁市高二下学期期末监测数学(理)试题Word版: 这是一份2022-2023学年四川省遂宁市高二下学期期末监测数学(理)试题Word版,共10页。试卷主要包含了考试结束后,将答题卡收回,分别求适合下列条件的方程,如下折线图等内容,欢迎下载使用。












