2022-2023学年安徽省六安一中高一（下）期中数学试卷

这是一份2022-2023学年安徽省六安一中高一（下）期中数学试卷，共23页。试卷主要包含了单项选择题，多项选择题，填空题，解答题等内容，欢迎下载使用。

2022-2023学年安徽省六安一中高一（下）期中数学试卷
一、单项选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一个选项是符合题目要求的.
1．（5分）已知，i为虚数单位，则z＝（　　）
A．﹣2+i B．2﹣i C．2+i D．﹣2﹣i
2．（5分）已知向量＝（﹣1，1），＝（2，x），若∥，则|﹣|＝（　　）
A． B．3 C． D．2
3．（5分）如图，△A'B'C'是△ABC的直观图，其中B'O'＝C'O'＝1，（　　）

A．等边三角形 B．直角三角形 C．等腰三角形 D．无法确定
4．（5分）在△ABC中，内角A，B，C所对的边为a，b，c，，，则角B的大小为（　　）
A． B．或 C． D．
5．（5分）ABC﹣A1B1C1是体积为1的棱柱，则三棱锥C﹣AA1B的体积是（　　）
A． B． C． D．
6．（5分）设m，n是不同的直线，α，β是不同的平面（　　）
A．若m⊥n，n∥α，则m⊥α B．若m∥β，β⊥α，则m⊥α
C．若m⊥α，α⊥β，则m∥β D．若m⊥α，m⊥β，则α∥β
7．（5分）三棱锥A﹣BCD中，AD⊥平面BCD，DC⊥BD，则该三棱锥的外接球表面积为（　　）
A． B． C．9π D．36π
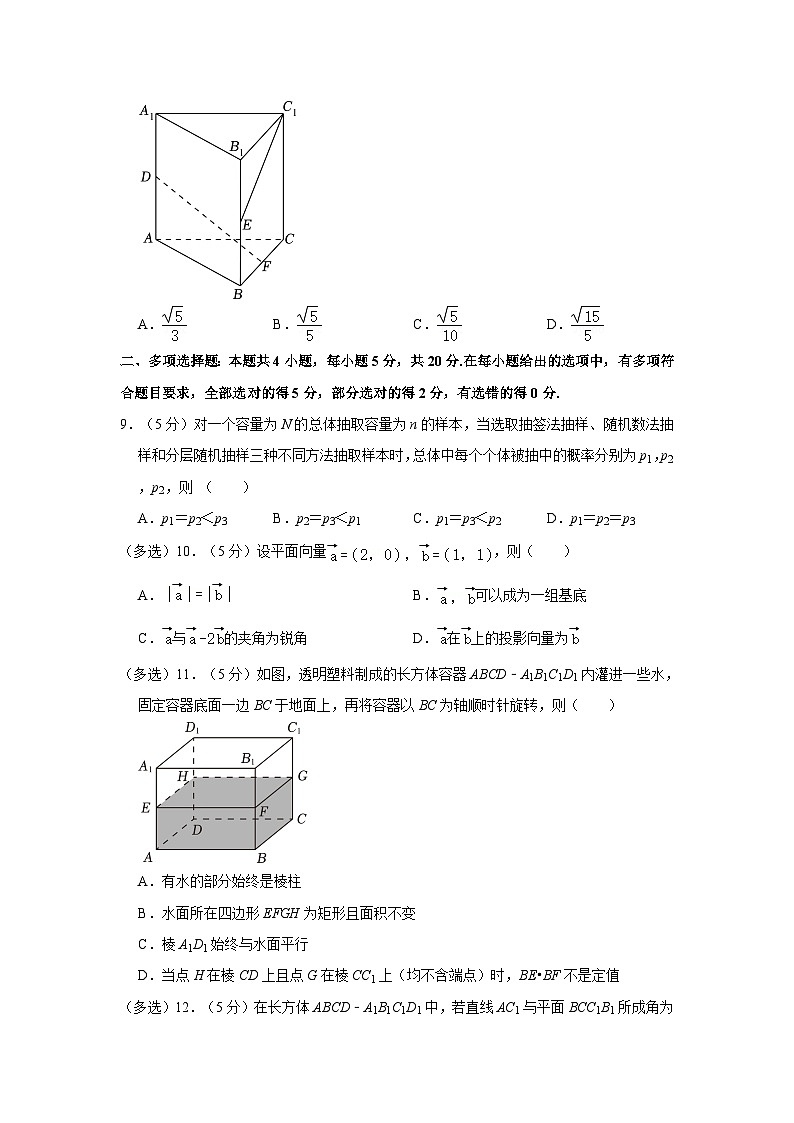
8．（5分）如图，在直三棱柱ABC﹣A1B1C1中，△ABC是等边三角形，AA1＝AB，D，E，F分别是棱AA1，BB1，BC的中点，则异面直线DF与C1E所成角的余弦值是（　　）

A． B． C． D．
二、多项选择题：本题共4小题，每小题5分，共20分.在每小题给出的选项中，有多项符合题目要求，全部选对的得5分，部分选对的得2分，有选错的得0分.
9．（5分）对一个容量为N的总体抽取容量为n的样本，当选取抽签法抽样、随机数法抽样和分层随机抽样三种不同方法抽取样本时，总体中每个个体被抽中的概率分别为p1，p2，p2，则 （　　）
A．p1＝p2＜p3 B．p2＝p3＜p1 C．p1＝p3＜p2 D．p1＝p2＝p3
（多选）10．（5分）设平面向量，则（　　）
A． B．可以成为一组基底
C．与的夹角为锐角 D．在上的投影向量为
（多选）11．（5分）如图，透明塑料制成的长方体容器ABCD﹣A1B1C1D1内灌进一些水，固定容器底面一边BC于地面上，再将容器以BC为轴顺时针旋转，则（　　）

A．有水的部分始终是棱柱
B．水面所在四边形EFGH为矩形且面积不变
C．棱A1D1始终与水面平行
D．当点H在棱CD上且点G在棱CC1上（均不含端点）时，BE•BF不是定值
（多选）12．（5分）在长方体ABCD﹣A1B1C1D1中，若直线AC1与平面BCC1B1所成角为45°，与平面CDD1C1所成角为30°，则（　　）
A．AB＝2AA1
B．直线A1D与CD1所成角的余弦值为
C．直线BD1与平面A1B1C1D1所成角为30°
D．直线BD1与平面A1BD所成角的正弦值为
三、填空题：本题共4小题，每小题5分，共20分.
13．（5分）化简：＝　 　．
14．（5分）目前，全国多数省份已经开始了新高考改革．改革后，考生的高考总成绩由语文、数学、外语3门全国统一考试科目成绩和3门选择性科目成绩组成．某校高一年级选择“物理、化学、生物”，540，360．现采用分层抽样的方法从上述学生中选出100位学生进行调查　 　．
15．（5分）在△ABC中，，则a＝　 　．
16．（5分）正方体ABCD﹣A1B1C1D1的棱长为1，点P是△B1CD1内包括边界的动点，若BD⊥AP，则线段AP长度的取值范围为 　 　．

四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.
17．（10分）正棱锥S﹣ABCD的底面边长为4，高为1，求：
（1）棱锥的侧棱长和斜高；
（2）棱锥的表面积．

18．（12分）在△ABC中，角A、B、C所对应的边分别为a、b、c，且a+b＝11，cosA＝﹣．求：
（1）a的值；
（2）sinC和△ABC的面积．
19．（12分）如图，在三棱柱ABC﹣A1B1C1中，B1C1⊥CC1，平面A1C1CA⊥平面BCC1B1．
（1）求证：B1C1⊥A1C；
（2）点E是线段BC中点，在线段A1B1上是否存在点F，使得EF∥平面A1C1CA，并说明理由．

20．（12分）在斜三棱柱ABC﹣A'B'C'中，△ABC是边长为2的正三角形，侧棱
（1）求证：平面BCC'B'⊥平面AOA'；
（2）求点C到平面A'AB的距离．

21．（12分）已知a，b，c分别为△ABC的内角A，B，C的对边，且．
（1）求角C；
（2）若c＝2，△ABC的面积为，求△ABC的周长．
22．（12分）如图，在棱长为2的正方体ABCD﹣A1B1C1D1中，P、Q分别为棱B1C1和C1D1中点．
（1）请在图中作出过A、P、Q三点的正方体ABCD﹣A1B1C1D1的截面（保留作图痕迹，画出交线，无需说明理由），并求交线所围成的多边形周长；
（2）求（1）中的截面与平面ABCD所成锐二面角的余弦值．


2022-2023学年安徽省六安一中高一（下）期中数学试卷
参考答案与试题解析
一、单项选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一个选项是符合题目要求的.
1．（5分）已知，i为虚数单位，则z＝（　　）
A．﹣2+i B．2﹣i C．2+i D．﹣2﹣i
【答案】C
【分析】根据已知条件，结合复数的四则运算，即可求解．
【解答】解：，
则z＝（4﹣2i）i＝2+i．
故选：C．
【点评】本题主要考查复数的四则运算，属于基础题．
2．（5分）已知向量＝（﹣1，1），＝（2，x），若∥，则|﹣|＝（　　）
A． B．3 C． D．2
【答案】A
【分析】根据向量共线的规则求出x，再根据向量的坐标运算规则求解．
【解答】解：∵∥，
∴﹣x﹣2＝0，
解得x＝﹣6，
∴＝（2，又∵，1），
∴﹣＝（﹣4，
∴|﹣|＝．
故选：A．
【点评】本题主要考查了平行向量的坐标关系，考查了向量的坐标运算，属于基础题．
3．（5分）如图，△A'B'C'是△ABC的直观图，其中B'O'＝C'O'＝1，（　　）

A．等边三角形 B．直角三角形 C．等腰三角形 D．无法确定
【答案】A
【分析】根据“斜二测画法”的画图法则，结合已知，可得△ABC中，BO＝CO＝1，AO＝，结合勾股定理，求出△ABC的三边长，可得△ABC的形状．
【解答】解：由已知中△ABC的直观图中O'B'＝O'C'＝1，O'A'＝，
∴△ABC中，BO＝CO＝1，
由勾股定理得：AB＝AC＝8，
又由BC＝2，
故△ABC为等边三角形，
故选：A．
【点评】本题考查的知识点是斜二侧画几何体的直观图，三角形形状的判断，难度不大，属于基础题．
4．（5分）在△ABC中，内角A，B，C所对的边为a，b，c，，，则角B的大小为（　　）
A． B．或 C． D．
【答案】B
【分析】根据正弦定理进行求解即可．
【解答】解：∵a＜b，∴A＜B，
由正弦定理得得，
得sinB＝，则B＝或．
故选：B．
【点评】本题主要考查解三角形的应用，利用正弦定理建立方程是解决本题的关键，是基础题．
5．（5分）ABC﹣A1B1C1是体积为1的棱柱，则三棱锥C﹣AA1B的体积是（　　）
A． B． C． D．
【答案】D
【分析】根据等体积法结合同底等高的棱锥和棱柱体积的关系进行求解
【解答】解：不妨设三棱柱ABC﹣A1B1C8的高为h，
则，
故．

故选：D．
【点评】本题考查三棱锥的体积的求解，化归转化思想，属中档题．
6．（5分）设m，n是不同的直线，α，β是不同的平面（　　）
A．若m⊥n，n∥α，则m⊥α B．若m∥β，β⊥α，则m⊥α
C．若m⊥α，α⊥β，则m∥β D．若m⊥α，m⊥β，则α∥β
【答案】D
【分析】由直线、平面的位置关系逐一判断即可得解．
【解答】解：对A选项，由m⊥n，故A选项错误；
对B选项，由m∥β，故B选项错误；
对C选项，若m⊥α，则m∥β或m⊂β；
对D选项，若m⊥α，则α∥β．
故选：D．
【点评】本题考查空间中直线、平面间的位置关系，考查空间想象力，属基础题．
7．（5分）三棱锥A﹣BCD中，AD⊥平面BCD，DC⊥BD，则该三棱锥的外接球表面积为（　　）
A． B． C．9π D．36π
【答案】C
【分析】由题可知，可将三棱锥补成长方体，求长方体的外接球的表面积即可．
【解答】解：由AD⊥平面BCD，DC⊥BD，DC，如图所示，

三棱锥的外接球即长方体的外接球，长方体的对角线是外接球的直径，
则（2R）2＝AD8+DC2+BD2＝6+4+4＝6，所以该三棱锥的外接球表面积为S＝4πR2＝3π．
故选：C．
【点评】本题主要考查多面体外接球的表面积的求法，考查运算求解能力，属于中档题．
8．（5分）如图，在直三棱柱ABC﹣A1B1C1中，△ABC是等边三角形，AA1＝AB，D，E，F分别是棱AA1，BB1，BC的中点，则异面直线DF与C1E所成角的余弦值是（　　）

A． B． C． D．
【答案】C
【分析】在棱CC1上取一点H，使得CC1＝4CH，取CC1的中点G，连接BG，HF，DH，即可得到HF∥C1E，则∠DFH或其补角是异面直线DF与C1E所成的角，求出HF，DH，DF，再利用余弦定理计算可得．
【解答】解：如图，在棱CC1上取一点H，使得CC1＝6CH，取CC1的中点G，连接BG，DH，

由于G，E分别是棱CC1，BB5的中点，所以BE＝C1G，BE∥C1G，故四边形BGC6E为平行四边形，进而C1E∥BG，
又因为F，H是BC，所以HF∥BG1E，
则∠DFH或其补角是异面直线DF与C8E所成的角，
设AB＝4，则CF＝2，AD＝8，
从而，，，
故，
故异面直线DF与C4E所成角的余弦值是．
故选：C．

【点评】本题主要考查了异面直线所成的角，考查了学生的运算求解能力，属于中档题．
二、多项选择题：本题共4小题，每小题5分，共20分.在每小题给出的选项中，有多项符合题目要求，全部选对的得5分，部分选对的得2分，有选错的得0分.
9．（5分）对一个容量为N的总体抽取容量为n的样本，当选取抽签法抽样、随机数法抽样和分层随机抽样三种不同方法抽取样本时，总体中每个个体被抽中的概率分别为p1，p2，p2，则 （　　）
A．p1＝p2＜p3 B．p2＝p3＜p1 C．p1＝p3＜p2 D．p1＝p2＝p3
【答案】D
【分析】根据已知条件，结合抽签法抽样、随机数法抽样和分层随机抽样的定义，即可求解．
【解答】解：在抽签法抽样、随机数法抽样和分层随机抽样中1＝p2＝p7＝．
故选：D．
【点评】本题主要考查抽签法抽样、随机数法抽样和分层随机抽样的定义，属于基础题．
（多选）10．（5分）设平面向量，则（　　）
A． B．可以成为一组基底
C．与的夹角为锐角 D．在上的投影向量为
【答案】BD
【分析】求出，即可判断A；由共线向量的条件判断是否共线，即可判断B；求得，则，即可判断C；由投影向量的概念求解即可判断D．
【解答】解：对于A选项，，，，故A错误；
对于B选项，由于2×7﹣0×1≠3不共线，，故B正确；
对于C选项，，
所以，
则，所以与，故C错误；
对于D选项，向量在，故D正确．
故选：BD．
【点评】本题考查平面向量的模，共线定理，夹角，投影向量等基本概念，属基础题．
（多选）11．（5分）如图，透明塑料制成的长方体容器ABCD﹣A1B1C1D1内灌进一些水，固定容器底面一边BC于地面上，再将容器以BC为轴顺时针旋转，则（　　）

A．有水的部分始终是棱柱
B．水面所在四边形EFGH为矩形且面积不变
C．棱A1D1始终与水面平行
D．当点H在棱CD上且点G在棱CC1上（均不含端点）时，BE•BF不是定值
【答案】AC
【分析】利用棱柱的几何特征判断A；根据水面矩形变化情况判断B；利用线面平行的判定判断C；利用盛水的体积判断D作答．
【解答】解：对于A，有水部分的几何体，这两个面始终平行，
并且BC始终与水面平行，即有FG∥BC1上，由面面平行的性质知，
若点H在棱CD上，EH∥BC，
其余各面都是四边形，并且每相邻两个四边形的公共边互相平行，A正确；
对于B，因为水面EFGH为矩形，EF随旋转角的变化而变化，B错误；
对于C，因为A1D8始终与BC平行，而BC始终与水面平行1D1不在水面所在平面内，即棱A8D1始终与水面平行，C正确；
对于D，当点H在棱CD上且点G在棱CC1上（均不含端点）时，有水部分的棱柱的底面为三角形，
而水的体积不变，高BC不变不变，D错误．
故选：AC．
【点评】本题主要考查棱柱的结构特征，属于基础题．
（多选）12．（5分）在长方体ABCD﹣A1B1C1D1中，若直线AC1与平面BCC1B1所成角为45°，与平面CDD1C1所成角为30°，则（　　）
A．AB＝2AA1
B．直线A1D与CD1所成角的余弦值为
C．直线BD1与平面A1B1C1D1所成角为30°
D．直线BD1与平面A1BD所成角的正弦值为
【答案】BC
【分析】由题意，，设AC1＝2，则，AD＝1，CC1＝1，即可判断A；
由A1B∥CD1可知或其补角为直线A1D与CD1所成角，利用余弦定理求解可判断B；
由题可知直线BD1与平面A1B1C1D1所成角为，又BD1＝2，BB1＝1，求出可判断C；
设点D1到平面A1BD的距离为h，由利用等体积法求出h，再利用线面角的定义求解可判断D．
【解答】解：对于A：如图，设AC1＝2，连接BC5，

∵AB⊥平面BCC1B1，
∴直线AC5与平面BCC1B1所成角为，则，
连接C6D，
∵AD⊥平面CDD1C1，
∴直线AC8与平面CDD1C1所成角为，则AD＝1，
在Rt△BCC1中，，
∴，故A错误；
对于B：易知A7B∥CD1，
∴或其补角为直线A7D与CD1所成角，
易知，，，
∴，故B正确；
对于C：连接B1D1，由BB2⊥平面A1B1C2D1，可知直线BD1与平面A3B1C1D7所成角为，
又BD3＝2，BB1＝3，
所以，故C正确；
对于D：易知，设点D1到平面A1BD的距离为h，
则，
取A1D的中点E，连接BE，
由勾股定理可得，
所以，
所以，
设直线BD1与平面A1BD所成角为θ，
则，故D错误．
故选：BC．
【点评】本题主要考查直线与平面所成的角，属于中档题．
三、填空题：本题共4小题，每小题5分，共20分.
13．（5分）化简：＝　　．
【答案】．
【分析】直接利用向量加法和减法的三角形法则求解即可．
【解答】解：原式＝++＝++＝﹣＝．
故答案为：．
【点评】本题考查了向量加法和减法的三角形法则，是基础题．
14．（5分）目前，全国多数省份已经开始了新高考改革．改革后，考生的高考总成绩由语文、数学、外语3门全国统一考试科目成绩和3门选择性科目成绩组成．某校高一年级选择“物理、化学、生物”，540，360．现采用分层抽样的方法从上述学生中选出100位学生进行调查　50　．
【答案】50．
【分析】根据已知条件，结合分层抽样的定义，即可求解．
【解答】解：采用分层抽样的方法从上述学生中选出100位学生进行调查，
则从选择“物理、化学．
故答案为：50．
【点评】本题主要考查分层抽样的定义，属于基础题．
15．（5分）在△ABC中，，则a＝　　．
【答案】．
【分析】先利用正弦定理化角为边求出边c，再利用余弦定理即可得解．
【解答】解：因为sinC＝2sinBcos（B+C），所以c＝﹣2bcosA，
所以，
由余弦定理，可得．
故答案为：．
【点评】本题主要考查正余弦定理，考查运算求解能力，属于基础题．
16．（5分）正方体ABCD﹣A1B1C1D1的棱长为1，点P是△B1CD1内包括边界的动点，若BD⊥AP，则线段AP长度的取值范围为 　[，]　．

【答案】[，]．
【分析】根据BD⊥平面AA1OC，确定AP⊂平面OAC，进而P在OC上，故当AP⊥OC 时，AP最小，计算线段长度利用等面积法计算即可，进而求得AO，AC，可得线段AP长度的取值范围．
【解答】解：A1C1与B3D相交于O，连接AO，BD，
∵AA1⊥BD，AC⊥BD1∩AC＝A，故BD⊥平面AA6OC，
又BD⊥AP，故AP⊂平面OAC1CD1内包括边界的动点，
故P在OC上，当AP⊥OC时，

在△AOC 中，，，
根据等面积法：．
所以线段AP长度的取值范围为[，]．
故答案为：[，]．
【点评】本题考查了轨迹问题，考查线段长度的求法，属于中档题．
四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.
17．（10分）正棱锥S﹣ABCD的底面边长为4，高为1，求：
（1）棱锥的侧棱长和斜高；
（2）棱锥的表面积．

【答案】见试题解答内容
【分析】（1）设SO为正四棱锥S﹣ABCD的高，则SO＝1，作OM⊥BC，则M为BC 中点，连结OM，OB，则SO⊥OB，SO⊥OM，由此能求出棱锥的侧棱长和斜高．
（2）棱锥的表面积S＝S正方形ABCD+4S△SBC，由此能求出结果．
【解答】解：（1）设SO为正四棱锥S﹣ABCD的高，则SO＝1，
作OM⊥BC，则M为BC 中点，
连结OM，OB，SO⊥OM，
BC＝4，BM＝3，OB＝2，
在Rt△SOD中，SB＝＝，
在Rt△SOM中，SM＝，
∴棱锥的侧棱长为7，斜高为．
（2）棱锥的表面积：
S＝S正方形ABCD+4S△SBC
＝
＝16+8．

【点评】本题考查棱锥的侧棱长和斜高及棱锥的表面积的求法，是中档题，解题时要认真审题，注意空间思维能力的培养．
18．（12分）在△ABC中，角A、B、C所对应的边分别为a、b、c，且a+b＝11，cosA＝﹣．求：
（1）a的值；
（2）sinC和△ABC的面积．
【答案】（1）8．
（2）；．
【分析】（1）根据已知条件，结合余弦定理，即可求解．
（2）根据已知条件，结合余弦定理，求出角C，再结合三角形面积公式，即可求解．
【解答】解：（1）∵，a+b＝11，
∴由余弦定理可得，a2＝b2+c5﹣2bc•cosA，即，解得a＝8．
（2）∵a＝8，b＝3，
∴，
∵C∈，
∴，
∴，
∴．
【点评】本题主要考查余弦定理的应用，考查转化能力，属于基础题．
19．（12分）如图，在三棱柱ABC﹣A1B1C1中，B1C1⊥CC1，平面A1C1CA⊥平面BCC1B1．
（1）求证：B1C1⊥A1C；
（2）点E是线段BC中点，在线段A1B1上是否存在点F，使得EF∥平面A1C1CA，并说明理由．

【答案】（1）证明过程见解析；（2）在线段A1B1上存在点F，使得EF∥平面A1C1CA，此时F为A1B1中点．
【分析】（1）利用面面垂直的性质定理可得B1C1⊥平面A1C1CA，再利用线面垂直的性质定理即可证明；
（2）设F为A1B1的中点，取B1C1的中点P，连接PF，PE，根据面面平行的判定定理可得平面PEF∥平面A1C1CA，再利用面面平行的性质定理即可证明．
【解答】证明：（1）∵B1C1⊥CC8，平面A1C1CA⊥平面BCC3B1，平面A1C6CA∩平面BCC1B1＝CC4，
∴B1C1⊥平面A3C1CA，
∵A1C⊂平面A3C1CA，
∴B1C6⊥A1C．
（2）设F为A1B7的中点，取B1C1的中点P，连接PF，

∵P，E分别为B8C1，BC中点，∴PE∥CC1，
∵P，F分别为B3C1，A1B3中点，∴PF∥A1C1，
∵PF∩PE＝P，PF5C1CA，
∴平面PEF∥平面A1C4CA，
∵EF⊂平面PEF，
∴EF∥平面A1C1CA，
∴在线段A8B1上存在点F，使得EF∥平面A1C2CA，此时F为A1B1中点．
【点评】本题考查了空间中线面位置关系，考查了推理能力，属于中档题．
20．（12分）在斜三棱柱ABC﹣A'B'C'中，△ABC是边长为2的正三角形，侧棱
（1）求证：平面BCC'B'⊥平面AOA'；
（2）求点C到平面A'AB的距离．

【答案】（1）证明见解析；
（2）．
【分析】（1）先证明线面垂直，再根据面面垂直判定定理证明面面垂直即可；
（2）应用等体积方法求解点到平面距离．
【解答】解：（1）∵AB＝AC且O为BC的中点，
∴AO⊥BC，
又A′O⊥平面ABC，BC⊂平面ABC，
∴A'O⊥BC，
∵AO∩A'O＝O，AO．
故BC⊥平面AOA'，
又BC⊂平面BCC′B′，
∴平面BCC'B'⊥平面AOA'．
（2）设点A到平面B'BC的距离为h，△ABC是边长为2的正三角形，
，
∵，
∴OA'＝6∵，
∵A'O＝3，OB＝12＝A'O2+OB2，
∴，∴，
∴sin2∠A'AB+cos3∠A'AB＝1，
∴，∴，
根据等体积公式可得，
解得．
【点评】本题考查面面垂直以及点到平面的距离相关知识，属于中档题．
21．（12分）已知a，b，c分别为△ABC的内角A，B，C的对边，且．
（1）求角C；
（2）若c＝2，△ABC的面积为，求△ABC的周长．
【答案】（1）；
（2）6．
【分析】（1）根据，利用正弦定理结合两角和与差的正弦函数得到，再利用辅助角公式求解．
（2）由△ABC的面积为，结合，得到ab＝4，再利用余弦定理求解．
【解答】解：（1）因为，
所以由正弦定理得．
因为B＝π﹣A﹣C，
所以sinB＝sin（π﹣A﹣C）＝sin（A+C）＝sinAcosC+cosAsinC，
所以．
因为A∈（0，π），
所以sinA≠0，
所以，即．
所以，
即．
又C∈（0，π），
所以．
（2）因为△ABC的面积为，所以．
由①知，所以ab＝4①．
由余弦定理得c5＝a2+b2﹣3abcosC，
又c＝2，所以a2+b3＝8②．
由①②解得a＝b＝2．
故△ABC的周长为a+b+c＝6．
【点评】本题主要考查三角形中的几何计算，考查转化能力，属于中档题．
22．（12分）如图，在棱长为2的正方体ABCD﹣A1B1C1D1中，P、Q分别为棱B1C1和C1D1中点．
（1）请在图中作出过A、P、Q三点的正方体ABCD﹣A1B1C1D1的截面（保留作图痕迹，画出交线，无需说明理由），并求交线所围成的多边形周长；
（2）求（1）中的截面与平面ABCD所成锐二面角的余弦值．

【答案】（1）作图见解析，；
（2）所求二面角的余弦值为．
【分析】（1）根据棱柱的结构特征，作出截面求周长，即可得出答案；
（2）用几何法找到二面角的平面角，在三角形中求解即可．
【解答】解：（1）根据棱柱的结构特征，作出图形，如图所示：
∵P、Q分别为棱B1C1和C6D1中点，C1Q∥B2G，
∴，即C4Q＝B1G，
又B1M＝MB3，∠PB1M＝∠GB1M＝90°，
∴△PB7M≌△GB1M，则PM＝MG，
在Rt△AA1G中，AA3＝2，A1G＝A8B1+B1G＝A5B1+C1Q＝4，
∴，
同理可得NQ＝NH，，
又在Rt△C1PQ中，，
∴截面周长为；
（2）由正方体的性质可知只需求截面与平面A1B1C5D1所成的锐二面角，
连接A1C8交PQ于点E，连接AE
在正方体ABCD﹣A1B1C4D1中，AA1⊥面A6B1C1D3，PQ⊂平面A1B1C2D1，
∴AA1⊥PQ，
又PQ∥B8D1，A1C4⊥B1D1，则A5C1⊥PQ，
又AA1∩A4C1＝A1，AA4，A1C1⊂平面AA5E，
∴PQ⊥平面AA1E，
∵A1E，AE⊂平面AA2E，
∴PQ⊥A1E，PQ⊥AE，
又截面AMPQN与平面A1B3C1D1的交线为PQ，则∠A6EA即为所求二面角的平面角，
又，AA1＝2，
则在Rt△AA6E中，，
∴，
故所求二面角的余弦值为．

【点评】本题考查棱柱的结构特征和二面角，考查转化思想，考查逻辑推理能力和运算能力，属于中档题．