【同步讲义】人教版数学七年级下册：第05章 重难点突破训练：相交线平行线类型题举例（99题123页）讲义

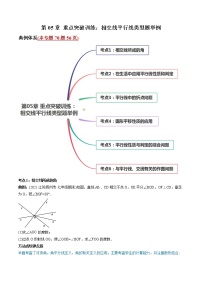
这是一份【同步讲义】人教版数学七年级下册：第05章 重难点突破训练：相交线平行线类型题举例（99题123页）讲义，文件包含同步讲义人教版数学七年级下册第05章重点突破训练相交线平行线类型题举例99题123页学生版docx、同步讲义人教版数学七年级下册第05章重点突破训练相交线平行线类型题举例99题123页教师版docx等2份试卷配套教学资源，其中试卷共163页， 欢迎下载使用。

第05章 重点突破训练：相交线平行线类型题举例

典例体系（本专题99题123页）
考点1：相交线所成的角
典例：（2022春·湖北荆州·七年级统考期末）如图，直线AB，CD相交于点O，OB平分∠EOD．

(1)若∠BOD＝30°，求∠EOC的度数；
(2)若∠BOD∶∠EOC＝1∶3，求∠AOD的度数；
(3)在（2）的条件下，画射线OF，若∠COF=90°，请直接写出∠BOF的度数．
【答案】(1)
(2)
(3)的度数为或
【分析】（1）先根据角平分线的定义可得，再根据平角的定义即可得；
（2）先根据可得，再根据平角的定义可得，然后根据邻补角的定义即可得；
（3）分两种情况讨论：①射线在的上方和②射线在的下方，先利用平角的定义可得，再根据角的和差即可得．
（1）解：因为平分，，所以，所以．
（2）解：因为，所以，因为，所以，所以，所以．
（3）解：由题意，分以下两种情况：①如图，当射线在的上方时，
因为，所以，所以；②如图，当射线在的下方时，

因为，所以，所以，综上，的度数为或．
方法或规律点拨
本题考查了与角平分线有关的计算、邻补角、平角，熟练掌握角平分线的运算是解题关键．
巩固练习
1．（2022秋·河北邢台·七年级统考期末）如图，直线AB，CD相交于点O，射线OM平分∠AOC，若∠BOD＝80°，则∠BOM等于（    ）

A．40° B．80° C．100° D．140°
【答案】D
【分析】根据对顶角相等和平角的定义即可求出∠AOC和∠BOC，然后根据角平分线的定义即可求出∠COM，从而求出结论．
【详解】解：∵
∴∠AOC=∠BOD=80°，∠BOC=180°－∠BOD=100°
∵平分
∴∠COM=∠AOC=40°
∴∠BOM=∠COM＋∠BOC=140°
故选:D．
【点睛】此题考查的是角的和与差，掌握对顶角相等、平角的定义和角平分线的定义是解决此题的关键．
2．（2022春·七年级单元测试）如图，直线、、相交于点，且，平分，若，则的度数为（    ）

A． B． C． D．无法确定
【答案】B
【分析】根据对顶角相等可以得到，再根据垂直的性质可以得到，即可求出的度数，再根据角平分线的定义即可得出答案．
【详解】解：∵，
∴
∵，
∴
∴
∵平分，
∴
故选B．
【点睛】本题考查了角度的和差倍分，垂直的定义，角平分线的定义，熟练掌握以上性质并找出角度之间的关系是本题的关键．
3．（2022秋·湖南湘西·七年级统考期末）如图，直线a，b相交于点O，如果，那么是____________°．

【答案】145
【分析】根据对顶角相等求出∠1，再根据互为邻补角的两个角的和等于180°列式计算即可得解．
【详解】解：∵，（对顶角相等），
∴，
∵∠1与∠3互为邻补角，
∴．
故答案为：．
【点睛】本题考查了对顶角相等的性质，邻补角的定义，是基础题，熟记概念与性质并准确识图是解题的关键．
4．（2022春·江苏·七年级专题练习）如图，直线与相交于点O，．

(1)如果，求和的度数；
(2)如果，求的度数．
【答案】(1)；
(2)

【分析】（1）根据角的和差与对顶角即可求解；
（2）根据已知条件可得，从而可求得，根据邻补角即可求的度数．
【详解】（1）∵，
∴，
∵与是对顶角，
∴．
（2）∵，
∴．
又∵，
∴，
∴，
∴．
【点睛】本题考查了对顶角，邻补角，以及角的和差计算，解答的关键是熟记对顶角与邻补角的定义的掌握与应用．
5．（2022秋·重庆·七年级校联考阶段练习）如图，直线，相交于点O，平分，平分．

(1)判断与的位置关系，并进行证明．
(2)若，求的度数．
【答案】(1)，证明见解析
(2)

【分析】（1）由平分，平分，得到，，根据邻补角互补可得出，进而可得出，由此即可证出；
（2）由，，得到，由对顶角相等，可求出，根据平分，平分，可得出以及，根据邻补角互补结合，可求出的度数．
【详解】（1）．
证明：∵平分，平分，
∴，，
∵，
∴，
∴．
（2）∵，，
∴，
∴，
∵，
∴，
∵平分，平分，
∴，．
∵，
∴，
∴．
【点睛】本题考查了对顶角相等，邻补角互补，角平分线的定义，熟练掌握知识点是解题的关键．
6．（2021春·湖北荆州·七年级统考期末）如图，O是直线AB上一点，平分．

(1)若，请求出的度数；
(2)若和互余，且，请求出的度数．
【答案】(1)
(2)

【分析】(1)根据角平分线的定义，即可求得；
(2)首先根据和互余，可得，再根据，可求得，可求得，据此即可求得．
（1）
解：，平分，，
；
（2）
解：和互余，
，
∴，
平分，
，
．
【点睛】本题考查了与角平分线有关的计算，准确找到角与角之间的关系是解决本题的关键．
7．（2022·全国·七年级专题练习）如图，直线AB、CD相交于点O，OE平分∠BOD，OF平分∠COE．

(1)若∠AOC=76°，求∠BOF的度数；
(2)若∠BOF=36°，求∠AOC的度数；
【答案】(1)∠BOF=33°
(2)∠AOC=72°

【分析】（1）先根据对顶角相等求出∠BOD=76°，再由角平分线定义得∠DOE=∠BOE=38°，由邻补角得∠COE=142°，再根据角平分线定义得∠EOF=71°，从而可得结论．
（2）利用角平分的定义得出，进而表示出各角求出答案．
【详解】（1）∵∠AOC、∠BOD是对顶角，
∴∠BOD=∠AOC=76°，
∵OE平分∠BOD，
∴∠DOE=∠BOE=∠BOD=38°
∴∠COE=142°，
∵OF平分∠COE．
∴∠EOF=∠COE=71°，
又∠BOE+∠BOF=∠EOF，
∴∠BOF=∠EOF−∠BOE=71°−38°=33°，
（2）∵OE平分∠BOD，OF平分∠COE，
∴，
∴设，则，
故，，
则，
解得，
故∠AOC=72°．
【点睛】本题考查了角平分线的定义和对顶角的性质，解决本题的关键是掌握对顶角的定义（从一个角的顶点引出一条射线，把这个角分成两个完全相同的角，这条射线叫做这个角的角平分线）．
8．（2022春·广东湛江·九年级校考期中）如图，已知O为直线上一点，过点O向直线上引三条射线，且平分．

(1)若平分，求的度数；
(2)若，，求的度数．
【答案】(1)
(2)

【分析】（1）利用角平分线的定义，可证得，，再根据邻补角的定义，就可求出的度数．
（2）根据已知及角平分线的定义，用含的代数式表示出，再根据，建立关于的方程，求解即可．
（1）
解：∵平分，OE平分∠BOC，
∴，，
∵
∴
答：的度数为．
（2）
解：∵，
∴
∵平分
∴
∵
∴
解之：
答：的度数为．
【点睛】本题考查了角平分线定义、平角以及角的计算等知识，熟练掌握角平分线定义是解题的关键．
9．（2022秋·福建龙岩·七年级校考阶段练习）如图，直线AB、CD相交于点O，∠DOE＝∠BOD，OF平分∠AOE．

(1)判断OF与OD的位置关系，并说明理由；
(2)若∠AOC：∠AOD＝1：5，求∠EOF的度数．
【答案】(1)OF⊥OD，理由见解析；
(2)∠EOF＝60°

【分析】（1）利用角平分线的定义结合已知求出∠FOD＝90°即可得出答案；
（2）求出∠AOC的度数，再利用对顶角的性质和角平分线的定义求出∠BOD＝∠AOC＝∠EOD＝30°，进而得出∠EOF的度数．
（1）
解：OF⊥OD，
理由：∵OF平分∠AOE，
∴∠AOF＝∠FOE，
∵∠DOE＝∠BOD，
∴∠AOF＋∠BOD＝∠FOE＋∠DOE＝×180°＝90°，即∠FOD＝90°，
∴OF与OD的位置关系是OF⊥OD；
（2）
∵∠AOC：∠AOD＝1：5，
∴∠AOC＝×180°＝30°，
∴∠BOD＝∠AOC＝∠EOD＝30°，
∴∠AOE＝120°，
∴∠EOF＝∠AOE＝60°．
【点睛】此题主要考查了角平分线的定义以及邻补角的性质，正确得出各角之间的关系是解题关键．
10．（2022春·七年级课时练习）如图，直线AB，CD相交于点O，OB平分∠EOD．

(1)若∠BOE：∠EOC＝1：4，求∠AOC的度数；
(2)在（1）的条件下，画OF⊥CD，请直接写出∠EOF的度数．
【答案】(1)
(2)或

【分析】（1）设，则，先根据角平分线的定义可得，，再根据邻补角的定义求出的值，从而可得的度数，然后根据对顶角相等即可得；
（2）先求出，再分①点在的上方和②点在的下方两种情况，根据角的和差即可得．
【详解】（1）解：由题意，设，则，
平分，
，，
，
，
解得，
，
由对顶角相等得：．
（2）解：由（1）可知，，
，
，
由题意，分以下两种情况：
①如图，当点在的上方时，

则；
②如图，当点在的下方时，

则；
综上，的度数为或．
【点睛】本题考查了与角平分线有关的计算、对顶角相等、一元一次方程的应用，较难的是题（2），正确分两种情况讨论是解题关键．
11．（2022秋·山东济宁·七年级统考期末）如图，直线 AB，CD相交于点O，∠BOC=80°，OE是∠BOC的平分线，OF是OE的反向延长线．

(1)求∠2、∠3的度数；
(2)说明 OF平分∠AOD的理由．
【答案】(1)∠2＝100°，∠3＝40°
(2)理由见详解

【分析】（1）根据邻补角的性质，得∠2＝180°﹣80°＝100°，再求出∠AOD的度数，根据角平分线的性质求出∠3；
（2）根据对顶角相等以及角平分线的定义得出∠AOF＝∠DOF即可．
（1）
解：∵∠2和∠BOC互为补角，且∠BOC＝80°，
∴∠2＝180°﹣80°＝100°，
∵OE是∠EOC的平分线，
∴∠1＝∠EOC＝ ∠BOC＝40°，
∵OF是OE的反向延长线，
∴∠3＝∠EOC＝40°，
（2）
理由如下：
由（1）得∠3＝∠EOC＝40°，
又∵∠AOF＝∠1＝40°，
∴∠AOF＝∠DOF，
∴OF平分∠AOD．
【点睛】本题考查角平分线的定义，对顶角、邻补角，理解角平分线的定义，掌握对顶角相等以及邻补角的性质是解题的关键．
12．（2022秋·湖北孝感·七年级统考期中）如图，直线与相交于点，．

(1)若，判断与的位置关系，并证明；
(2)若，求的度数．
【答案】(1)
(2)

【分析】（1）根据垂直的定义求解即可；
（2）根据角的和差及“对顶角相等”求解即可．
（1）
，理由如下：
，
，
，
，
，
即，
；
（2）
，，
，
，
，
，
．
【点睛】此题考查了对顶角、邻补角，熟记对顶角、邻补角的概念是解题的关键．
13．（2022春·陕西安康·七年级统考期末）如图，点在直线上，与互补，平分．

(1)若，则的度数为______；
(2)若，求的度数．
【答案】(1)
(2)

【分析】（1）根据互补的定义，邻补角以及角平分线的定义解答即可；
（2）根据互补的定义和角平分线的定义列出方程解答即可．
（1）
解：∵点在直线上，，
∴，
∵与互补，
∴，
∵平分，
∴，
∴．
故答案为：．
（2）
设为x，
∵点在直线上，
∴与互补，
∵与互补，
∴，
∵平分，
∴，
∴，
∵与互补，
即，
，
解得：，
∴．
∴的度数为．
【点睛】本题考查补角问题，涉及互补的定义，邻补角，等角的补角相等，角平分线的定义．理解和掌握互补的定义，邻补角以及角平分线的定义是解题的关键．
14．（2022春·七年级课时练习）如图1，点为直线上一点，过点作射线，使．将一直角三角板的直角顶点放在点处，一边在射线上，另一边在直线的下方．

(1)将图1中的三角板绕点处逆时针旋转至图2，使一边在的内部．且恰好平分，求的度数；
(2)在图3中，延长线段得到射线，判断是否平分，请说明理由．
(3)将图1中的三角板绕点按每秒10°的速度沿顺时针方向旋转一周，在旋转的过程中，第秒时，直线恰好平分锐角，则的值为______．（直接写出答案）
【答案】(1)
(2)平分；理由见解析
(3)30或12秒

【分析】（1）由角的平分线的定义和等角的余角相等求解；
（2）先由对顶角性质得=30°，再由，得，从而得出结论；
（3）由∠BOC=120°可得∠AOC=60°，则∠AON=30°或∠NOR=30°，即顺时针旋转300°或120°时ON平分∠AOC，据此求解．
【详解】（1）解：∵，
∴，
∵恰好平分，
∴，
∴，
∴；
（2）解：∵（对顶角），．
∴，
又∵，
∴．
∴
∴平分
（3）解：30或12．
设三角板绕点旋转的时间是秒，
∵，
∴，
如图，当的反向延长线平分时，

，
∴，
∴旋转的角度是，
∴，
∴；
如图，当平分时，

，
∴旋转的角度是，
∴，
∴，
综上，或，
即此时三角板绕点旋转的时间是30或12秒．
【点睛】此题考查了角的计算，关键是应该认真审题并仔细观察图形，找到各个量之间的关系，是解题的关键．
15．（2022秋·浙江台州·七年级校联考阶段练习）如图，直线CD，EF相交于点O，射线OA在∠COF的内部，∠DOF=∠AOD．

(1)如图1，若∠AOC=120°，求∠EOC的度数；
(2)如图2，若∠AOC=α（60°<α<180°），将射线OA绕点O逆时针旋转60°，到OB，
①求∠EOB的度数（用含α的式子表示）；
②观察①中的结果，直接写出∠AOC，∠EOB之间的数量关系．
(3)如图3 ，0°<∠AOC <120°，将射线OA绕点O顺时针旋转60°，到OB，请直接写出∠AOC，∠EOB之间的数量关系．
【答案】(1)∠EOC＝20°；
(2)①∠EOB＝；②∠EOB＝∠AOC；
(3)当0°<∠AOC ≤90°时，∠EOB＝∠AOC＋120°；当90°<∠AOC ≤120°时，∠EOB＝240°－∠AOC．

【分析】（1）根据补角的定义求出∠AOD，结合已知求出∠DOF，然后根据对顶角相等得出答案；
（2）①根据补角的定义求出∠AOD，结合已知求出∠DOF，然后根据对顶角相等求出∠EOC，再根据∠BOC＝α－60°，求出∠EOB的度数即可；②根据题意结合补角的定义求出∠AOD＝180°－∠AOC，∠BOC＝∠AOC－60°，然后可得∠DOF＝∠AOD＝60°－∠AOC，再根据对顶角相等计算得出答案；
（3）分情况讨论：①当0°<∠AOC ≤90°时，根据题意结合补角的定义求出∠AOD＝180°－∠AOC，∠BOC＝∠AOC＋60°，然后可得∠DOF＝∠AOD＝60°－∠AOC，再根据对顶角相等计算得出答案；②当90°<∠AOC ≤120°时，根据题意结合补角的定义求出∠AOD＝180°－∠AOC，∠BOC＝∠AOC＋60°，然后可得∠DOF＝∠AOD＝60°－∠AOC，再根据对顶角相等计算得出∠EOC＋∠BOC＝∠AOC＋120°，最后根据周角的定义计算得出答案．
（1）
解：∵∠AOC＝120°，
∴∠AOD＝180°－∠AOC＝180°－120°＝60°，
∴∠DOF＝∠AOD＝20°，
∴∠EOC＝∠DOF＝20°；
（2）
解：①∵∠AOC＝α，
∴∠AOD＝180°－α，
∴∠DOF＝∠AOD＝60°－，
∴∠EOC＝∠DOF＝60°－，
由题意得：∠AOB＝60°，
∴∠BOC＝α－60°，
∴∠EOB＝∠EOC＋∠BOC＝60°－＋α－60°＝；
②观察①中结果可得：∠EOB＝，
证明：∵∠AOD＝180°－∠AOC，∠BOC＝∠AOC－∠AOB＝∠AOC－60°，
∴∠DOF＝∠AOD＝60°－∠AOC，
∴∠EOC＝∠DOF＝60°－∠AOC，
∴∠EOB＝∠EOC＋∠BOC＝60°－∠AOC＋∠AOC－60°＝∠AOC；
（3）
解：①当0°<∠AOC ≤90°时，
如图，∵∠AOD＝180°－∠AOC，∠BOC＝∠AOC＋∠AOB＝∠AOC＋60°，
∴∠DOF＝∠AOD＝60°－∠AOC，
∴∠EOC＝∠DOF＝60°－∠AOC，
∴∠EOB＝∠EOC＋∠BOC＝60°－∠AOC＋∠AOC＋60°＝∠AOC＋120°．

②当90°<∠AOC ≤120°时，
如图，∵∠AOD＝180°－∠AOC，∠BOC＝∠AOC＋∠AOB＝∠AOC＋60°，
∴∠DOF＝∠AOD＝60°－∠AOC，
∴∠EOC＝∠DOF＝60°－∠AOC，
∴∠EOC＋∠BOC＝60°－∠AOC＋∠AOC＋60°＝∠AOC＋120°，
∴∠EOB＝360°－（∠EOC＋∠BOC）＝360°－∠AOC－120°＝240°－∠AOC．

【点睛】本题考查了补角的定义，角的和差计算，对顶角相等，理清各角之间的关系是正确计算的前提．
考点2：补全证明过程
典例：（2022春·黑龙江哈尔滨·七年级哈尔滨市第六十九中学校校考期中）完成下面推理过程.
在括号内、横线上填空或填上推理依据．
如图，已知：，，，求证：．

证明：∵（已知）
∴______（______）
∵（已知）
∴______（______）
即
∴
∵（已知）
∴______（______）
∴EF∥______（______）
∴（______）．
【答案】；两直线平行，内错角相等；90°；垂直定义；；同角的余角相等；；内错角相等，两直线平行；平行于同一条直线的两条直线互相平行或如果两条直线都与第三条直线平行，那么这两条直线也互相平行．
【分析】根据平行线的性质得到，根据余角的性质得到，根据平行线的判定定理即可得到结论．
【详解】证明：∵（已知），
∴（两直线平行，内错角相等），
∵（已知），
∴90°（垂直定义），
即，
∴，
∵（已知），
∴（同角的余角相等），
∴EF∥CD（内错角相等，两直线平行），
∴（平行于同一条直线的两条直线互相平行或如果两条直线都与第三条直线平行，那么这两条直线也互相平行）．

方法或规律点拨
本题考查了平行线的判定和性质，垂直的定义，熟练掌握平行线的判定和性质是解题的关键．
巩固练习
1．（2022春·吉林长春·七年级期末）如图，直线，，，求的度数．

阅读下面的解答过程，并填空（理由或数学式）．
解：∵（已知），
∴（        ）（                    ）．
又∵，（已知），
∴（等式的性质）．
∴（        ）．
∴（        ）（        ）（                ）．
∴（        ）（                ）．
∴．
【答案】，两直线平行，内错角相等，等量代换，，，同旁内角互补，两直线平行，，两直线平行，同位角相等．
【分析】根据题干的提示，利用平行线的判定与性质逐步填写理由，从而可得答案．
【详解】解：∵（已知），
∴（两直线平行，内错角相等）．
又∵，（已知），
∴（等式的性质）．
∴（ 等量代换 ）．
∴（ 同旁内角互补，两直线平行）．
∴（两直线平行，同位角相等）．
∴．
【点睛】本题考查的是平行线的判定与性质，熟记平行线的判定方法与性质是解本题的关键．
2．（2022春·吉林长春·七年级吉林大学附属中学期末）根据题意，完成推理填空：如图，，，试说明．

解：∵（已知）
∴______（内错角相等，两直线平行）
∴（两直线平行，同旁内角互补）
∵（已知）
∴______＋______，（    ）
∴（等量代换）
【答案】；；；两直线平行，同旁内角互补
【分析】根据平行线的性质和平行线的判定解答．
【详解】解：∵（已知）
∴（内错角相等，两直线平行）
∴（两直线平行，同旁内角互补）
∵（已知）
∴，（两直线平行，同旁内角互补）
∴（等量代换）
故答案为：；；；两直线平行，同旁内角互补．
【点睛】本题主要考查平行线的性质和判定，解题的关键是灵活运用所学知识解决问题．
3．（2022春·八年级单元测试）（1）完成下面的推理说明：
已知：如图，，、分别平分和．
求证：．

证明：、分别平分和（已 知） ，
， （ ）．
（ ），
（ ）．
（ ）．
（等式的性质） ．
（ ）．
（2）说出（1）的推理中运用了哪两个互逆的真命题 ．
【答案】（1）；；角平分线的定义；已知；两直线平行，内错角相等；等量代换；内错角相等，两直线平行；（2） 两个互逆的真命题为：两直线平行，内错角相等；内错角相等，两直线平行
【分析】（1）根据平行线的性质，可得，根据角平分线的定义，可得，再根据平行线的判定，即可得出；
（2）在两个命题中，如果一个命题的结论和题干是另一个命题的题干和结论， 则称它们为互逆命题．
【详解】解： （1）、分别平分和（已知），
，（角平分线的定义），
（已知），
（两直线平行，内错角相等），
（等量代换），
（等式的性质），
（内错角相等，两直线平行），
故答案为：；；角平分线的定义；已知；两直线平行，内错角相等；等量代换；内错角相等， 两直线平行；
（2）两个互逆的真命题为：
两直线平行，内错角相等；内错角相等，两直线平行．
【点睛】本题考查的是平行线的判定与性质的运用，解题时注意：平行线的判定是由角的数量关系判断两直线的位置关系；平行线的性质是由平行关系来寻找角的数量关系．命题都是由题设和结论两部分组成，题设是已知事项，结论是由已知事项推出的事项．
4．（2022春·福建福州·七年级校考期末）如图，平分，F在上，G在上，与相交于点H，，试说明．（请通过填空完善下列推理过程）

解：∵（已知），（　　）
∴___________（等量代换）．
∴（　　）
∴______（___________）．
∵平分，
∴______（___________）．
∴（　　）
【答案】对顶角相等；；同旁内角互补，两直线平行；；两直线平行，同位角相等；；角平分线的定义；等量代换
【分析】求出，根据平行线的判定得出，根据平行线的性质得出，根据角平分线的定义得出即可．
【详解】解：∵（已知），（对顶角相等），
∴（等量代换），
∴（同旁内角互补，两直线平行），
∴（两直线平行，同位角相等），
∵平分，
∴（角平分线的定义），
∴（等量代换），
故答案为：对顶角相等；；同旁内角互补，两直线平行；；两直线平行，同位角相等；；角平分线的定义；等量代换．
【点睛】本题考查了平行线的性质和判定，角平分线的定义，能灵活运用平行线的性质和判定定理进行推理是解此题的关键．
5．（2021春·黑龙江哈尔滨·七年级哈尔滨市虹桥初级中学校校考期中）证明：∵，（已知）

∴（垂直定义）
∴（同位角相等，两直线平行）
∴___________（___________）
∵（已知）
∴（___________）
∴（同位角相等，两直线平行）
∴（___________）
∵（已知）
∴（垂直定义）
【答案】；两直线平行，内错角相等；等量代换；两直线平行，同位角相等
【分析】先证明,推出，再得到,再利用平行线的性质即可得到结论．
【详解】证明：∵，（已知）,

∴（垂直定义）,
∴（同位角相等，两直线平行）,
∴（两直线平行，内错角相等）,
∵（已知）,
∴（等量代换）,
∴（同位角相等，两直线平行）,
∴（两直线平行，同位角相等）,
∵（已知）,
∴（垂直定义）．
故答案为：；两直线平行，内错角相等；等量代换；两直线平行，同位角相等．
【点睛】本题考查了平行线的判定和性质，熟记平行线的判定和性质并准确识图是解题的关键．
6．（2022秋·山东济南·七年级统考期末）如图，，，，求的度数．

解：∵，
∴　 　（ 　 　）．
又∵，
∴（ 　 　）．
∴　 　（ 　 　）．
∴　 　（ 　 　）．
∵，
∴　 　．
【答案】；两直线平行，同位角相等；等量代换；；内错角相等，两直线平行；；两直线平行，同旁内角互补；
【分析】根据平行线的性质和已知求出，根据平行线的判定推出，根据平行线的性质求出即可．
【详解】解：∵，
∴（两直线平行，同位角相等．）
又∵，
∴（等量代换），
∴（内错角相等，两直线平行），
∴（两直线平行，同旁内角互补），
∵，
∴．
故答案为：；两直线平行，同位角相等；等量代换；；内错角相等，两直线平行；；两直线平行，同旁内角互补；．
【点睛】本题考查了平行线的性质和判定的应用，能灵活运用平行线的性质和判定定理进行推理是解此题的关键，注意：平行线的性质是①两直线平行，同位角相等，②两直线平行，内错角相等，③两直线平行，同旁内角互补，反之亦然．
7．（2022秋·北京·七年级校考阶段练习）如图所示的是一个潜望镜模型示意图，，代表镜子摆放的位置，并且与平行，光线经过镜子反射时，满足，．证明离开潜望镜的光线平行于进入潜望镜的光线．

请补全下述证明过程：
∵，
∴______（____________________________________）．
∵，，
∴．
∵，______，
∴______．
∴（____________________________________）．
【答案】；两直线平行，内错角相等；；内错角相等，两直线平行．
【分析】根据，可得，从而得到，进而得到，即可．
【详解】证明：∵，
∴（两直线平行，内错角相等）．
∵，，
∴．
∵，，
∴．
∴（内错角相等，两直线平行）．
故答案为：；两直线平行，内错角相等；；内错角相等，两直线平行．
【点睛】本题主要考查了平行线的判定和性质，熟练掌握平行线的判定和性质是解题的关键．
8．（2022秋·北京·七年级北京市第一六一中学校考期末）推理填空：如图，直线被直线所截，是的角平分线，若，求∠4的度数．
解：∵直线与直线相交，
∴．（ ）
∵是的角平分线，
∴，（ ）
∵，（已知）
∴，（等量代换）
∴，（等量代换）
∴，（ ）
∴ ，（两直线平行，同位角相等）

【答案】见解析
【分析】根据平行线的判定及性质求解，一步步把求解的过程补充完整即可．
【详解】解：∵直线与直线相交，
∴（对顶角相等），
∵是的角平分线，
∴，（角平分线的定义），
∵（已知），
∴（等量代换），
∴等量代换），
∴（内错角相等，两直线平行），
∴（两直线平行，同位角相等）．
故答案为：对顶角相等；角平分线的定义；内错角相等，两直线平行；．
【点睛】本题考查了平行线的判定及性质、角平分线的定义，解题的关键是把解题的过程补充完整．本题属于基础题，难度不大，解决该题型题目时，熟悉利用平行线的性质解决问题的过程．
9．（2022秋·湖南邵阳·七年级校考期中）已知，如图，平分平分．求证：．

请将下列证明过程中的空格补充完整．
证明：∵，
∴．（   ）
∵平分平分，
∴．（   ）
∴　 　．
∴．（   ）
∴　 　．（两直线平行，内错角相等）
∵，
∴，即．（   ）
【答案】两直线平行，同位角相等； 角平分线的定义；；同位角相等，两直线平行；；垂直的定义
【分析】根据，可得，再由平分平分，可得，从而得到，进而得到，即可．
【详解】证明：∵，
∴．（两直线平行，同位角相等）
∵平分平分，
∴．（角平分线的定义）
∴．
∴．（同位角相等，两直线平行）
∴．（两直线平行，内错角相等）
∵，
∴，即．（垂直的定义）
故答案为∶ 两直线平行，同位角相等； 角平分线的定义；；同位角相等，两直线平行；；垂直的定义
【点睛】本题主要考查了平行线的判定和性质，垂直的定义，熟练掌握平行线的判定和性质是解题的关键．
10．（2022秋·陕西渭南·七年级统考阶段练习）完成下面的证明：如图，点在上，，连接，平分，，于点．
求证：．

证明：∵，
∴（_____________________）．
∵，
∴，即．
∵平分，
∴______（__________________）．
∴，
∴（________________________）
∴__________________（________________________）．
∵，
∴______（______________________）．
∴．
【答案】两直线平行，内错角相等； ；角平分线的定义；内错角相等，两直线平行； ；两直线平行，内错角相等；90；垂直的定义

【分析】根据平行线性质与判定、角平分线定义、垂直的定义填空即可．
【详解】证明：∵，
∴（两直线平行，内错角相等）．
∵，
∴，即．
∵平分，
∴（角平分线的定义）．
∴，
∴（内错角相等，两直线平行）．
∴（两直线平行，内错角相等）．
∵，
∴（垂直的定义）．
∴．
故答案为：两直线平行，内错角相等；；角平分线的定义；内错角相等，两直线平行；；两直线平行，内错角相等；90；垂直的定义．
【点睛】本题主要考查了平行线的性质与判定，角平分线的定义，垂直的定义，熟知相关知识是解题的关键．
11．（2022春·黑龙江哈尔滨·七年级哈尔滨市第四十九中学校校考阶段练习）填空并在括号内加注理由．
已知：如图，，，，，求证：．

证明：∵，（已知）
∴（________________）
∴（________________）
∴________（________________）
∵（已知）
∴（________________）
∴（同位角相等，两直线平行）
∴________（________________）
∵（已知）
∴
∴
∴（________________）
【答案】垂直定义；同位角相等，两直线平行；；两直线平行，内错角相等；等量代换；；两直线平行，同位角相等；垂直定义
【分析】先证得，可得到，从而得到，进而得到，即可求证．
【详解】证明：∵，（已知）
∴（垂直定义）
∴（同位角相等，两直线平行）
∴（两直线平行，内错角相等）
∵（已知）
∴（等量代换）
∴（同位角相等，两直线平行）
∴（两直线平行，同位角相等）
∵（已知）
∴
∴
∴（垂直定义）
故答案为：垂直定义；同位角相等，两直线平行；；两直线平行，内错角相等；等量代换；；两直线平行，同位角相等；垂直定义
【点睛】本题主要考查了平行线的判定和性质，熟练掌握平行线的判定和性质是解题的关键．
考点3：在生活中应用平行线性质和判定
典例：（2022秋·广东深圳·七年级校考期中）如图，图①是一种网红弹弓的实物图，在两头上系上皮筋，拉动皮筋可形成平面示意图如图②和图③，弹弓的两边可看成是平行的，即，各活动小组探索与，之间数量关系时，有如下发现，

(1)在图②所示的图形中，若，，则___________
(2)在图⑧中，若，，则_________
(3)有同学在图②和图③的基础上，面出了图④所示的图形，其中，请判断，，之间的关系，并说明理由．
【答案】(1)
(2)
(3)

【分析】（1）如图所示，过点P作，利用平行线的性质得到由此即可得到答案；
（2）如图所示，过点P作，利用平行线的性质得到，在求出的度数即可得到答案；
（3）如图所示，过点P作，由平行线的性质得到，再由即可得到结论．
（1）
解：如图所示，过点P作，
∵，
∴，
∴，
∴，
故答案为：；

（2）
解：如图所示，过点P作，
∵，
∴，
∴，
∵，
∴
∴，
故答案为：；

（3）
解：，理由如下：
如图所示，过点P作，
∵，
∴，
∴，
∴，
∴．

方法或规律点拨
本题主要考查了平行线的性质，正确作出辅助线是解题的关键．
巩固练习
1．（2022秋·河北石家庄·七年级统考期中）有一道题目“一副直角三角尺如图所示叠放，现将含45°角的三角尺ADE固定不动，将含30°角的三角尺ABC绕顶点A顺时针转动180°，在旋转的过程中，当三角尺ABC的边BC与三角尺ADE的边平行时，求∠BAD．”嘉嘉的结果是∠BAD为60°或105°；淇淇说：“嘉嘉考虑的不周全，∠BAD还有另一个不同的值．”下列判断正确的是（    ）

A．淇洪说的对，且∠BAD的另一个值为15°
B．嘉嘉的结果完全正确
C．嘉嘉求的结果不对，∠BAD为30°或105°
D．两人都不对，∠BAD应5有个不同的值
【答案】A
【分析】分三种情况：若，若，若，由平行线的性质可得出答案．
【详解】解：若，
∴∠CFE=∠E=90°，
又∵∠C=30°，
∴，

∴∠DAB=45°-30°=15°；
若，

；
若，

，
．
综上所述，为或或．
故选：．
【点睛】本题考查了旋转的性质，平行线的性质，正确画出图形是解题的关键．
2．（2022秋·贵州安顺·七年级统考期末）如图，某沿湖公路有三次拐弯，若第一次的拐角∠A=110°，第二次的拐角∠B=140°，第三次的拐角为∠C，第三次拐弯后的道路恰好和第一次拐弯之前的道路平行，则∠C的度数是（    ）

A．130° B．140° C．145° D．150°
【答案】D
【分析】过点B作BEAD，利用平行线的性质可得∠ABE＝110°，从而求出∠EBC＝30°，然后再利用平行线的性质，即可解答．
【详解】解：过点B作BEAD，
∴∠A＝∠ABE＝110°，
∵∠ABC＝140°，
∴∠EBC＝∠ABC−∠ABE＝30°，
∵ADCF，
∴BECF，
∴∠C＝180°−∠EBC＝150°，
故选：D．

【点睛】本题考查了平行线的性质，根据题目的已知条件并结合图形添加适当的辅助线是解题的关键．
3．（2022秋·广东深圳·七年级校考期中）某同学在研究传统文化“抖空竹”时有一个发现：他把它抽象成数学问题，如图所示，已知，，，则的度数是 （  ）

A． B． C． D．
【答案】B
【分析】延长交于，依据，，可得，再根据三角形外角性质，即可得到．
【详解】解：如图，延长交于，

∵，，
，
又，，
．
故选：B．
【点睛】本题主要考查了平行线的性质，解决问题的关键是掌握：两直线平行，同位角相等．
4．（2022秋·河南商丘·七年级统考期末）在庆祝中华人民共和国成立70周年阅兵式上，我国自主研制的“DF—17导弹”首次登场，震撼全球．如图是“DF—17导弹”上的一个零件的平面图，已知AB∥FE∥DC，AF∥ED∥BC，∠B=65°，则等于（     ）

A．130° B．120° C．115° D．90°
【答案】A
【分析】根据平行线的性质进行角的转换即可求解；
【详解】解：∵AB∥DC，∠B=65°，
∴∠C=180°-∠B=180°-65°=115°，
∵ED∥BC，
∴∠D=180°-∠C=180°-115°=65°，
∵FE∥DC，
∴∠DEF=∠D=65°，
∵AF∥ED，
∴∠F=∠DEF=∠D=65°，
∴∠F+∠D=65°+65°=130°．
故选：A．
【点睛】本题主要考查平行线的性质，掌握平行线的性质并根据题意灵活应用是解题的关键．
5．（2022春·广东深圳·八年级校考期末）光线在不同介质中传播速度不同，从一种介质射向另一种介质时会发生折射．如图，水面与水杯下沿平行，光线从水中射向空气时发生折射，光线变成，点在射线上，已知，，则的度数为______．

【答案】##25度
【分析】根据平行线的性质求得，根据即可求解．
【详解】解：∵，
∴．
∵，
∴；
故答案为25°．
【点睛】本题考查了平行线的性质与判定，掌握平行线的性质与判定是解题的关键．
6．（2022秋·北京·七年级校考阶段练习）如图，一把长方形直尺沿直线断开并错位，点，，，在同一条直线上．若，则的度数是______．

【答案】##度
【分析】根据平行线的性质及邻补角的性质作答．
【详解】解：∵，
∴，
∵，
∴．
故答案为：．
【点睛】本题考查平行线的性质，解题关键是熟练掌握两直线平行，内错角相等．
7．（2022春·黑龙江哈尔滨·七年级哈尔滨德强学校校考期中）如图，汽车灯的剖面图，从位于点的灯发出光照射到凹面镜上反射出的光线，都是水平线，若，，则的度数为______．

【答案】##60度
【分析】如图所示，过点O作，则，根据平行线的性质求解即可．
【详解】解：如图所示，过点O作，

∵光线，都是水平线，
∴，
∴，
∴，
∴，
故答案为：．
【点睛】本题主要考查了平行线的性质，熟知两直线平行，内错角相等是解题的关键．
8．（2022春·北京海淀·八年级北京市十一学校校考期中）如图，平面中两条直线和相交于点，对于平面上任意一点，若点到直线、的距离分别是、，则称有序实数对是点的“距离坐标”．特别地，当点在直线上时，定义点到直线的距离为0．下列说法：
①“距离坐标”是的点只有点；
②“距离坐标”是的点只有1个；
③“距离坐标”是的点共有4个；
正确的有_________．（填序号）

【答案】①②③
【分析】根据“距离坐标”的定义逐条分析即可．
【详解】解：①若“距离坐标”为，则点有且仅有1个，是与的交点O，正确；
②如图所示，若“距离坐标”为，则，，的点有且仅有2个，点O的两侧直线上各有一个到直线距离为1的点，正确；

③若“距离坐标”为，则，，的点如图所示，过直线的一点作的平行线且到直线l2的距离等于2，过直线l2的一点作的平行线且到直线的距离等于1的直线相交于、、、，有且仅有4个，正确．
所以上述命题中，正确命题是：①②③．

【点睛】本题考查了新定义“距离坐标”、平行线的性质、点到直线的距离，简易逻辑的判定方法，考查了推理能力与作图能力，属于中档题．
9．（2022秋·山东济南·六年级校考期中）幸福乡要修建一条灌溉水渠，如图，水渠从A村沿北偏东60°的方向到B村，从B村沿北偏西30°方向到C村．若水渠从C村沿CD方向修建可以保持与AB的方向一致，则∠DCB的度数为_____°

【答案】90度##90°
【分析】根据CD与AB的方向一致，可得，即有∠DCB=∠CBA，根据，可得∠A+∠ABN=180°，即有∠ABC=90°，则有∠DCB=90°，问题得解．
【详解】如图，设置点M、N，

根据题意有：，
∵CD与AB的方向一致，
∴，
∴∠DCB=∠CBA，
∵，
∴∠A+∠ABN=180°，
∵∠A=60°，∠ABN=∠ABC+∠CBN，∠CBN=30°，
∴∠ABC=90°，
∴∠DCB=90°，
故答案为：90°．
【点睛】本题考查了平行线的性质、方位角的应用，明确题意，灵活运用平行线的性质是解答本题的关键．
10．（2022秋·陕西西安·七年级校考阶段练习）如图，将木条，与钉在一起，，，要使木条与平行，木条按图所示方向旋转的度数至少是 __．

【答案】30°
【分析】根据同位角相等，两直线平行，求出旋转后∠2的同位角的度数，然后用∠1减去即可得到木条a旋转的度数．
【详解】解：如图：

∵∠AOC＝∠2＝50°时，OA//b，即a//b，
∴要使木条a与b平行，木条a旋转的度数至少是80°﹣50°＝30°．
故答案为：30°．
【点睛】本题考查了平行线的判定，根据同位角相等两直线平行求出旋转后∠2的同位角的度数是解题的关键．
11．（2022秋·浙江温州·七年级统考期中）如图，放置在水平操场上的篮球架的横梁EF始终平行于AB，EF与上拉杆CF形成的∠F＝140°，主柱AD垂直于地面，通过调整CF和后拉杆BC的位置来调整篮筐的高度．当∠CDB＝35°时，点H，D，B在同一直线上，则∠H的度数是_.

【答案】##105度
【分析】过D点作DIEF，根据两直线平行，同旁内角互补可求∠FDI＝40°，根据平角的定义可求∠ADB＝15°，根据直角三角形的性质可求∠ABH＝75°，再根据两直线平行，同旁内角互补可求∠H＝105°．
【详解】解：过D点作DIEF，

∵∠F＝140°，
∴∠FDI＝40°，
∴∠ADB＝180°−90°−40°−35°＝15°，
∴∠ABH＝90°−15°＝75°．
∵GHAB，
∴∠H＝180°−75°＝105°．
故答案为：105°．
【点睛】本题考查了平行线的性质，平行线性质定理：两直线平行，同位角相等；两直线平行，同旁内角互补； 两直线平行，内错角相等．
12．（2022秋·山东泰安·六年级统考期末）如图1是某景区电动升降门，将其抽象为几何图形，如图2所示，垂直于地面于，当平行于地面时，则______．

【答案】270°##270度
【分析】过点B作BFAE，如图，由于CDAE，则BFCD，根据两直线平行，同旁内角互补得∠BCD＋∠CBF＝180°，由AB⊥AE得AB⊥BF，所以∠ABF＝90°，于是有∠ABC＋∠BCD＝∠ABF＋∠CBF＋∠BCD＝270°．
【详解】解：过点B作BFAE，如图：

∵CDAE，
∴BFCD，
∴∠BCD＋∠CBF＝180°，
∵AB⊥AE，
∴AB⊥BF，
∴∠ABF＝90°，
∴∠ABC＋∠BCD＝∠ABF＋∠CBF＋∠BCD＝90°＋180°＝270°．
故答案为：270°．
【点睛】本题主要考查了平行线的性质，正确作出辅助线，并熟记两直线平行，同旁内角互补是解决问题的关键．
13．（2022秋·福建三明·七年级校考期中）为了亮化某景点，三明市在两条笔直且互相平行的景观道MN、QP上分别放置A、B两盏激光灯，如图所示，A灯发出的光束自AM逆时针旋转至AN便立即回转，B灯发出的光束自BP逆时针旋转至BQ便立即回转，两灯不间断照射，A灯每秒转动30°，B灯每秒转动10°，B灯先转动4秒，A灯才开始转动，当B灯光束第一次到达BQ之前，两灯的光束互相平行时A灯旋转的时间是_______________秒．

【答案】2或8##8或2
【分析】设A灯旋转时间为t秒，B灯光束第一次到达BQ需要180÷10=18（秒），推出t≤18-4，即t≤14．利用平行线的判定，构建方程解决问题即可．
【详解】解：设A灯旋转时间为t秒，B灯光束第一次到达BQ需要180÷10=18（秒），
∴t≤18-4，即t≤14．
由题意，满足以下条件时，两灯的光束能互相平行：
①如图1，∠=∠，30t=10（4+t），
解得t=2；

②如图2，当A灯发出的光束旋转至AN回转时，
∠+∠=180°，30t-180+10（4+t）=180，
解得t=8；

综上所述，A灯旋转的时间为2或8秒．
故选：2或8．
【点睛】本题考查平行线的性质，解决此题的关键是分类讨论、有平行的性质列出每种情况的等量关系．
14．（2022秋·山东东营·六年级校考期末）实验证明，平面镜反射光线的规律是：射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等．如图1，一束光线m射到平面镜a上，被a反射后的光线为n，则入射光线m、反射光线n与平面镜a所夹的锐角．

(1)利用这个规律人们制作了潜望镜，图2是潜望镜工作原理示意图，AB、CD是平行放置的两面平面镜．已知光线经过平面镜反射时，有，，请解释进入潜望镜的光线m为什么和离开潜望镜的光线是平行的？（请把证明过程补充完整）
理由：∵（已知），
∴（① ），
∵，（已知），
∴（② ），
∴，即：，
∴（③ ）
(2)显然，改变两面平面镜AB、CD之间的位置关系，经过两次反射后，入射光线m与反射光线n之间的位置关系会随之改变，如图3，一束光线m射到平面镜AB上，被AB反射到平面镜CD上，又被CD反射．若被CD反射出的光线n和光线m平行，且，则∠6=______°，∠ABC=______°．
(3)请你猜想：图3中，当两平面镜AB、CD的夹角∠ABC=______°时，可以使任何入射光线m经过平面镜AB、CD的两次反射后，与反射光线n平行、请说明理由．
【答案】(1)①两直线平行，内错角相等；②等量代换；③内错角相等，两直线平行；
(2)96，90
(3)当时，可以使任何入射光线m经过平面镜AB、CD的两次反射后，与反射光线n平行，理由见解析

【分析】（1）根据两直线平行内错角相等得，根据角之间的关系等量代换得，即可得，根据内错角相等两直线平行即可得；
（2）由题意得，，，即可得，根据得，可得，即可得，根据三角形内角和定理即可得；
（3）由（1）得，，，根据，得，即可得，等量代换得即，根据三角形内角和定理即可得．
（1）
证明：∵（已知），
∴（①两直线平行，内错角相等 ），
∵，（已知），
∴（②等量代换 ），
∴，即：，
∴（③内错角相等，两直线平行 ）
故答案为：①两直线平行，内错角相等；②等量代换；③内错角相等，两直线平行；
（2）
解：由题意得，，，
∴，
∵，
∴，
∴，
∴，
∴，
故答案为：96，90．
（3）
当时，可以使任何入射光线m经过平面镜AB、CD的两次反射后，与反射光线n平行，理由如下：
解：由（1）得，，，
∵，
∴，
∴，


∴，
，
∴，
故答案为：．
【点睛】本题考查了平行线的判定与性质，解题的关键是理解题意，掌握平行线的判定与性质．
15．（2022秋·浙江台州·七年级校联考期中）如图1，MN、EF是两面互相平行的镜面，根据镜面反射规律，若一束光线AB照射到镜面MN上，产生反射光线BC，则一定有∠1＝∠2．试根据这一规律：

(1)利用直尺和量角器作出光线BC经镜面EF反射后的反射光线GH；
(2)在（1）的作图背景下，试判断AB与GH的位置关系，并说明理由．
(3)如图2，若∠1＝30°，有一镜面PQ，从PN开始绕着点P以3°/s的速度顺时针转动（0°＜＜180°），当转动多少秒时，光线照射到镜面PQ上，产生的反射光线与镜面MN平行？
(4)如图3，若∠1＝30°，∠NPQ＝（0°＜＜180°），光线经镜面EF反射后照射到镜面PQ上，产生的反射光线与入射光线的夹角为，请直接写出与之间的关系： ．
【答案】(1)见解析
(2)ABGH，理由见解析
(3)25秒或35秒
(4)或

【分析】（1）利用直尺和量角器作∠BGE＝∠GHF即可；
（2）证明∠ABG＝∠BGH，即可得到结论；
（3）设转动t秒时，产生的反射光线与镜面MN平行．分两种情况列方程求解即可；
（4）分三种情况分别求解即可．
（1）
如图1，

（2）
ABGH，
证明：由题意可得，
∠1＝∠2，∠EGB＝∠HGF，
∵MNEF，
∴∠2＝∠EGB，
∴∠1＝∠2＝∠EGB＝∠HGF，
∴180°∠2＝180°∠EGB ∠HGF，
即∠ABG＝∠BGH，
∴ABGH．
（3）
设转动t秒时，产生的反射光线与镜面MN平行．
①当BC经EF反射后照射到PQ．如图2，
               
可列出方程：，解得．
②BC直接照射到PQ．如图3，

可列出方程：，解得．
综上所述，设转动25秒或35秒时，产生的反射光线与镜面MN平行．
（4）
或，理由是：
当0°＜＜90°时，如图4，则∠JRT＝，作RSEF，

∵MNEF，
∴MNEFRS，
∴∠SRP＝∠NPQ＝，∠RTF＝∠SRT＝∠BTE＝∠2＝∠1＝30°，
∴∠PRT＝∠JRQ＝∠PRS＋∠SRT＝＋30°，
∴∠PRT＋∠TRJ＋∠JRQ＝2（＋30°）＋＝180°，
即．
当＝90°时，如图5，则∠JRT＝，

∵MNEF，
∴∠TSR＝∠SPN＝90°，∠1＝∠2＝∠BTE＝∠RTS＝30°，
∴∠TRS＝∠JRP＝60°，
∴∠JRT＝＝60°，
∴2－＝120°；
当90°＜＜180°时，如图6，则∠JRT＝，作RSEF，

∵MNEF，
∴MNEFRS，
∴∠SRP＝∠NPQ＝，∠RTF＝∠SRT＝∠BTE＝∠2＝∠1＝30°，
∴∠JRS＝∠JRT－∠SRT＝－30°，
∴∠JRP＝∠TRQ＝∠SRP－∠JRS＝－（－30°）＝－＋30°，
∵∠JRP＋∠TRQ＋∠JRT＝2（－＋30°）＋＝180°，
∴．
故答案为：或
【点睛】此题主要考查了平行线的判定和性质，熟练掌握平行线的判定和性质是解题的关键．
16．（2022春·全国·八年级专题练习）光线照射到镜面会产生反射现象，由光学知识，入射光线与镜面的夹角与反射光线与镜面的夹角相等，例如：在图1中，有∠1＝∠2．

(1)如图2，已知镜子MO与镜子ON的夹角∠MON＝90°，请判断入射光线AB与反射光线CD的位置关系，并说明理由；
(2)如图3，有一口井，已知入射光线AO与水平线OC的夹角为50°，当平面镜MN与水平线OC的夹角为 °，能使反射光线OB正好垂直照射到井底；
(3)如图4，直线EF上有两点A、C，分别引两条射线AB、CD．∠BAF＝120°，∠DCF＝40°，射线AB、CD分别绕A点、C点以3度/秒和1度/秒的速度同时逆时针转动，设时间为t秒，在射线AB转动一周的时间内，是否存在某时刻，使得CD与AB平行？若存在，求出所有满足条件的时间t．
【答案】(1)ABCD，理由见解析
(2)65或115
(3)在射线AB转动一周的时间内，存在时间t，使得CD与AB平行，其t=10s或100s．

【分析】（1）计算∠ABC+∠BCD的值便可得出结论；
（2）先计算出∠AOB，进而得∠AOM+∠BON的值，再根据入射光线与镜面的夹角与反射光线与镜面的夹角相等，得出结果；
（3）分四种情况讨论：当0s≤t≤20s时，当20s＜t≤40s时，当40s＜t≤80s时，当80s＜t≤120s时，根据角度大小变化关系锁确ABCD时的t值．
【详解】（1）解： ABCD．理由如下：
∵∠1=∠2，∠3=∠4，
∴∠ABC=180°-∠1-∠2=180°-2∠2，∠BCD=180°-∠3-∠4=180°-2∠3，
∴∠ABC+∠BCD=360°-2（∠2+∠3），
∵∠BOC=90°，
∴∠2+∠3=90°，
∴∠ABC+∠BCD=180°，
∴AB∥CD；
（2）解：∵∠AOC=40°，∠BOC=90°，
∴∠AOM+∠BON=180°-90°=40°=50°，
∵∠AOM=∠BON，
∴∠AOM=∠BON=25°，
∴∠COM=25°+40°=65°，∠CON=25°+90°=115°，
∴当平面镜MN与水平线OC的夹角为65°或115°时，能使反射光线OB正好垂直照射到井底，
故答案为：65或115；
（3）解：①当0s≤t≤20s时，如下图，

若ABCD，则∠BAC=∠ACD，
即120+3t=140+t，
解得t=10，
∴当t=10s时ABCD；
②当20s＜t≤40s时，如下图，

有∠BAE＜90°＜∠ACD，则AB与CD不平行；
③当40s＜t≤80s时，如下图，

有∠BAC＜∠ACD，AB与CD不平行；
④当80s＜t≤120s时，如下图，

若ABCD，则∠BAC=∠DCF，
即3t-240=t-40，
解得t=100，
∴当t=100s时，ABCD；
综上可知，在射线AB转动一周的时间内，存在时间t，使得CD与AB平行，其t=10s或100s．
【点睛】本题主要考查了平行线的性质与判定，关键是应用分类讨论思想解决问题．
考点4：平行线中的折点问题
典例：（2022秋·江西赣州·七年级统考期中）根据下列叙述填依据．
(1)已知如图1，，求∠B+∠BFD+∠D的度数．

解：过点F作
所以∠B+∠BFE=180°（                                          ）
因为、（已知）
所以 （                                           ）
所以∠D+∠DFE=180°（                                             ）
所以∠B+∠BFE+∠D=∠B+∠BFE+∠EFD +∠D=360°
(2)根据以上解答进行探索．如图（2）（3）ABEF、∠D与∠B、∠F有何数量关系（请选其中一个简要证明）
备用图：

(3)如图（4）ABEF，∠C=90°，∠与∠、∠有何数量关系（直接写出结果，不需要说明理由）

【答案】(1)两直线平行，同旁内角互补；，平行于同一直线的两直线平行；两直线平行，同旁内角互补
(2)见解析
(3)
【分析】（1）过点F作，得到∠B+∠BFE=180°，再根据、得到，∠D+∠DFE=180°，最后利用角度的和差即可得出答案；
（2）类比问题（1）的解题方法即可得解；
（3）类比问题（1）的解题方法即可得解．
（1）解：过点F作，如图，
∴∠B+∠BFE=180°（两直线平行，同旁内角相等），
∵、（已知）
∴（平行于同一直线的两直线平行），
∴∠D+∠DFE=180°（两直线平行，同旁内角互补），
∴∠B+∠BFE+∠D=∠B+∠BFE+∠EFD +∠D=360°；
故答案为：两直线平行，同旁内角互补；，平行于同一直线的两直线平行；
两直线平行，同旁内角互补；

（2）解：选图（2），∠D与∠B、∠F的数量关系为：∠BDF+∠B=∠F；
理由如下：

过点D作DC//AB，
∴∠B=∠BDC，
∵，，
∴，
∴∠CDF=∠F，
∴∠BDF+∠BDC =∠F，
即∠BDF+∠B=∠F；
选图（3），∠D与∠B、∠F的数量关系：∠BDF+∠B=∠F

过点D作，
∴∠B=∠BDC，
∵，，
∴，
∴∠CDF=∠F，
∴∠BDF+∠BDC =∠F，
即∠BDF+∠B=∠F
∠BDF+∠B=∠F ；
（3）解：

如图（4）所示，过点C作，过D作，
∴，，
∵，，
∴，
∴，
∵ ，，
∴．
方法或规律点拨
本题考查根据平行线的性质探究角的关系和平行线公理推论的运用，熟练掌握平行线的性质和平行线公理推论的运用是解题的关键．
巩固练习
1．（2022秋·重庆云阳·七年级校考阶段练习）如图，已知，，，那么等于（　　）

A． B． C． D．
【答案】B
【分析】过点C作，根据，得出，根据平行线的性质求出，，即可得出答案．
【详解】解：过点C作，如图所示：

∵，
∴，
∴，，
∴，故B正确．
故选：B．
【点睛】本题主要考查了平行线的性质，解题的关键是作出辅助线，熟练掌握两直线平行内错角相等；两直线平行同旁内角互补．
2．（2022春·四川雅安·八年级统考期末）如图，，，探索图中角α，β，γ之间的关系式正确的是（　　）

A． B． C． D．
【答案】B
【分析】首先过点C作，过点D作，由，即可得，然后由两直线平行，内错角相等，即可求得答案．
【详解】解：过点C作，过点D作，

∵，
∴，
∴，
∵，，
由①②得：．
即
故选：B．
【点睛】此题考查了平行线的性质．此题难度适中，注意掌握辅助线的作法，注意数形结合思想的应用是解题的关键．
3．（2022春·黑龙江哈尔滨·七年级哈尔滨市第六十九中学校校考期中）如图，，则下列各式中正确的是（    ）

A． B．
C． D．
【答案】D
【分析】根据平行线的性质（两直线平行，内错角相等、两直线平行，同旁内角互补）即可得到结论．
【详解】∵，
∴，，
∴，
∴，
故选：D．
【点睛】本题考查了平行线的性质，熟记性质是解题关键．
4．（2022秋·浙江杭州·七年级校考阶段练习）如图，，设，，正确的选项是（    ）

A．若，则
B．若，则
C．若，则
D．若，则
【答案】D
【分析】如图，利用平行线的判定和性质进行求解即可．
【详解】解：如图：的顶点分别为，延长交直线与点，
当，则，
∴，
∵，
∴，
∴，即：，解得：，
∴；
A、无法求出∠2的度数，选项错误，不符合题意；
B、无法求出∠3的度数，选项错误，不符合题意；
C、，，选项错误，不符合题意；
D、，选项正确，符合题意；
故选D．

【点睛】本题考查平行线的判定和性质，熟练掌握平行线的判定和性质是解题的关键．
5．（2022春·黑龙江哈尔滨·七年级哈尔滨风华中学校考期中）如图，已知，则___________．

【答案】
【分析】如图，过作 过作证明可得再证明从而可得答案．
【详解】解：如图，过作 过作

∵
∴
∴
∴
而
∴
∵
∴
∴
∴
∵
∴
∴
故答案为：
【点睛】本题考查的是平行公理的应用，平行线的性质，利用平行公理作出辅助线是解本题的关键．
6．（2022秋·重庆铜梁·七年级校考期中）如图，已知，且∠C=110°，则∠1与∠2的数量关系为__________________ .

【答案】
【分析】过点C作，则，根据平行线的性质可得角之间的关系，从而∠1与∠2的数量关系即可求解.
【详解】解：过点C作，如图：
则，

∴，，
∵，
∴，
∴，
∴.
故答案为：.
【点睛】本题考查了平行线的性质，解题的关键是作出平行线，利用平行线的性质得出角之间的关系.
7．（2022秋·甘肃武威·七年级校考期末）如图，若ABCD，则，，则______．

【答案】##20度
【分析】过点作，利用平行线的性质可得的度数，进而可得的度数，再结合可得，进而可得的度数．
【详解】解：如图，过点作，则，

，
，
，
．
故答案为：．
【点睛】本题主要考查平行线的性质，构造合适的辅助线是解题关键．
8.（2022春·八年级课时练习）已知：如图，，求证：．

【答案】见解析
【分析】根据平行线的性质定理，进而得出，则，即可得出．
【详解】证明：过点C作，
∴，
∵，
∴，
∴，
∴．

9.（2022春·八年级课时练习）已知：如图，求证：．

【答案】见解析
【分析】过点P作，即得出，再根据平行线的性质可得出，，最后由，即可证．
【详解】证明：如图，过点P作．

∴．
∵，
∴，
∴．
∵，
∴．
10．（2022秋·贵州毕节·七年级校考期中）已知：如图，，，，，求的度数．

【答案】
【分析】根据平行线的性质可得，再由可得出答案．
【详解】解：∵，，
∴，∠C=∠ABC=65°，
∴．
【点睛】本题考查平行线的性质，关键要掌握两直线平行，内错角相等、同旁内角互补．
11．（2022秋·重庆铜梁·七年级校考阶段练习）课题学习：平行线的“等角转化”功能．

(1)阅读理解：如图1，已知点A是外一点，连接、，求的度数．阅读并补充下面推理过程．
解：过点A作，
， ，
，
．
解题反思：从上面的推理过程中，我们发现平行线具有“等角转化”的功能，将、、“凑”在一起，得出角之间的关系，使问题得以解决．
(2)方法运用：如图2，已知，求的度数；
(3)深化拓展：已知，点C在点D的右侧，，平分，平分，，所在的直线交于点E，点E在直线与之间．
①如图3，点B在点A的左侧，若，求的度数．
②如图4，点B在点A的右侧，且，．若，求度数．（用含n的代数式表示）
【答案】(1)；
(2)
(3)①；②

【分析】（1）由“两直线平行，内错角相等”可得结果；
（2）过C作，利用“两直线平行，同旁内角互补”可以求得结果；
（3）①过E作，利用角平分线的概念求得，，再利用“两直线平行，内错角相等”导角即可；②过E作，利用角平分线的概念求得，，再利用平行线的性质导角即可．
【详解】（1）解：，
，（两直线平行，内错角相等）；
故答案为：；
（2）解：过C作，
，
，
，
，
，
，
；
（3）解：①过E作，
，
，
，
平分，
，
，
平分，
，
，
，
；
②过E作，
，
，
，
平分，，
，
，
，
，
．

【点睛】本题考查了平行线的性质、平行线的传递性以及角平分线的概念，作出辅助线构造平行线导角是解决本题的关键．
12．（2022秋·山东德州·七年级校考期中）请阅读小明同学在学习平行线这章知识点时的一段笔记，然后解决问题．
小明：老师说在解决有关平行线的问题时，如果无法直接得到角的关系，就需要借助辅助线来帮助解答，今天老师介绍了一个“美味”的模型一“猪蹄模型”．即
已知：如图1，，为、之间一点，连接，得到．

求证：，
小明笔记上写出的证明过程如下：
证明：过点作，
∴，
∵，，
∴
∴，
∵，
∴，
请你利用“猪蹄模型”得到的结论或解题方法，完成下面的两个问题．
(1)如图2，若，，求的度数；
(2)灵活应用：如图3，一条河流的两岸当小船行驶到河中点时，与两岸码头B、D所形成的夹角为（即），当小船行驶到河中点时，恰好满足，，请你直接写出此时点与码头B、D所形成的夹角＝_________．
【答案】(1)240°
(2)32°
【分析】（1）过E点作，过F点作，易得，，，则有∠B=∠BEN，∠NEF=∠EFM，∠C+∠CFM=180°，根据∠BEN+∠NEF=∠BEF，∠EFM+∠CFM=∠EFC，∠BEF=60°，即有∠B+∠EFC+∠C=(∠B+∠EFM)+(∠CFM+∠C)=∠BEF+180°=240°；
（2）根据题目的证明方法可得∠F=∠ABF+∠CDF，∠E=∠ABE+∠CDE，由∠ABF=∠EBF，∠EDF=∠CDF，可得∠ABF=∠ABE，∠CDF=∠CDE，即有∠F=∠ABF+∠CDF=(∠ABE+∠CDE)=，问题得解．
（1）
过E点作，过F点作，如图，

∵，，，
∴，，，
∴∠B=∠BEN，∠NEF=∠EFM，∠C+∠CFM=180°，
∵∠BEN+∠NEF=∠BEF，∠EFM+∠CFM=∠EFC，∠BEF=60°，
∴∠B+∠EFC+∠C=(∠B+∠EFM)+(∠CFM+∠C)=∠BEF+180°=240°，
故答案为：240°；
（2）
根据题目中“猪蹄模型”的证明方法，同理可以证明：∠F=∠ABF+∠CDF，∠E=∠ABE+∠CDE，
∵∠E=64°，
∴∠ABE+∠CDE=64°，
∵∠ABF=∠EBF，∠EDF=∠CDF，
∴∠ABF=∠ABE，∠CDF=∠CDE，
∵∠F=∠ABF+∠CDF，
∴∠F=∠ABF+∠CDF=(∠ABE+∠CDE)=，
故答案为：32°．
【点睛】本题主要考查了平行线的性质，掌握两直线平行，内错角相等，同旁内角互补是解答本题的关键．

考点5：图形平移性质的应用
典例：16．（2022·全国·七年级专题练习）如图，在三角形中，，，，，将三角形沿方向平移得到三角形，且与相交于点，连接．

（1）阴影部分的周长为______；
（2）若三角形的面积比三角形的面积大，则的值为______．
【答案】          ####
【分析】（1）由平移的性质可得出，．再根据，即可求出阴影部分的周长；
（2）过A点作于，利用等面积法计算出，由，，即可得出，再根据，即可列出关于a的等式，解出a即可．
【详解】（1）∵三角形沿方向平移得到三角形，
，．
，
阴影部分的周长为，
故答案为：；
（2）过A点作于，如图，

∵∠BAC=90°
∴，
∴．
∵，
∴．
∵，
∴，
∴，即．
∵三角形的面积比三角形的面积大，即，
∴，
解得．
故答案为：．
方法或规律点拨
本题考查平移的性质，平行四边形的面积，三角形的面积．掌握平移的性质是解决（1）的关键，正确作出辅助线是解决（2）的关键．
巩固练习
1．（2022秋·辽宁丹东·八年级校考期末）如图，将沿BC方向平移3cm得到，若的周长为24cm，则四边形ABFD的周长为（    ）

A．30cm B．24cm C．27cm D．33cm
【答案】A
【分析】根据平移的性质可得DF=AC，再求出四边形ABFD的周长等于△ABC的周长加上AD与CF，然后计算即可得解．
【详解】解：∵△ABC沿BC方向平移3cm得到△DEF，
∴DF=AC，AD=CF=3cm，
∴



=30（cm）
故选：A．
【点睛】本题主要考查了平移的基本性质：①平移不改变图形的形状和大小；②经过平移，对应点所连的线段平行且相等，对应线段平行且相等，对应角相等，确定出四边形的周长与△ABC的周长的关系是解题的关键．
2．（2022春·上海静安·七年级上海市市西中学校考期中）如图，将周长为厘米的沿射线方向平移厘米得到，那么四边形的周长为___________厘米．

【答案】
【分析】利用平移的性质得到，然后根据可计算出四边形的周长．
【详解】解：沿射线方向平移厘米得到，
，
，
cm．
即四边形的周长为．
故答案为．
【点睛】本题考查了平移的性质：把一个图形整体沿某一直线方向移动，会得到一个新的图形，新图形与原图形的形状和大小完全相同．新图形中的每一点，都是由原图形中的某一点移动后得到的，这两个点是对应点．连接各组对应点的线段平行或共线且相等．
3．（2022春·上海宝山·七年级校联考期末）已知线段的长度为9厘米，现将线段向左平移5厘米得到线段，点A对应点C，点B对应点D，且A，B，C，D在同一直线上，那么的长度是____厘米
【答案】
【分析】根据平移的性质直接求解即可．
【详解】解：经过平移，将线段向左平移5厘米得到线段，如图，

∴（厘米），而（厘米），
则（厘米）．
故答案为：14．
【点睛】本题利用了线段的和差关系，平移的基本性质：①平移不改变图形的形状和大小；②经过平移，对应点所连的线段平行（或在同一直线时）且相等，对应线段平行（或在同一直线时）且相等．
4．（2022秋·广东东莞·七年级东莞市光明中学校考期中）如图，某酒店重新装修后，准备在大厅主楼梯上铺设红色地毯，其侧面如图所示，则需地毯 __米．

【答案】8
【分析】根据平移的性质，即可求出大厅主楼梯上铺设红色地毯的长．
【详解】解：由平移的性质可知，
所需要的地毯的长度为，
故答案为：8．
【点睛】本题考查了生活中的平移现象，熟练掌握平移的性质是解题的关键．
5．（2022秋·北京海淀·七年级校考阶段练习）如图，一块边长为8米的正方形土地，在上面修了三条道路，宽都是1米，其余部分种上各种花草，则种植花草的面积是____平方米．

【答案】42
【分析】直接利用平移方法，将三条道路平移到图形的一侧，进而求出即可．
【详解】解：

（平方米）．
故种植花草的面积是42平方米．
故答案为：42．
【点睛】本题考查了生活中的平移现象，图形的平移只改变图形的位置，而不改变图形的形状和大小，学生易混淆图形的平移与旋转或翻转，以致错误．
6．（2022春·山东青岛·九年级统考期中）如图，两个直角三角形重叠在一起，将其中一个沿点到点的方向平移到的位置，，，平移距离为6，则阴影部分的面积为______．

【答案】48
【分析】先利用平移和平行线截线段成比例定理求出线段的长度，再利用面积公式求出两个三角形的面积，再求差即可．
【详解】由平行可知， ,
则
∵
∴
∴
∴

故填48．
【点睛】本题考查平移和平行线截线段成比例定理，关键是求出所需线段的长度．
7．（2022春·黑龙江哈尔滨·七年级哈尔滨德强学校校考期中）如图，，将直角三角形沿着射线方向平移4cm，得到三角形，已知，，则阴影部分面积为______．

【答案】
【分析】根据平移的性质求出的长，再根据梯形面积公式求解即可．
【详解】解：由平移的性质可得，
∴，
∵，
∴，
∴，
故答案为：．
【点睛】本题主要考查了平移的性质，梯形面积，熟知平移的性质是解题的关键３．
8．（2022春·黑龙江大庆·九年级统考期中）如图，直角三角形的周长为，在其内部有个小直角三角形，且这个小直角三角形都有一条边与平行，则这个小直角三角形周长的和为_________．

【答案】
【分析】根据题意得这个小直角三角形都有一条边与平行，则有小直角三角形中与平行的边的和等于，与平行的边的和等于BC，则小直角三角形的周长和等于直角的周长，据此即可求解．
【详解】解：因为这个小直角三角形都有一条边与平行，，
所以这个小直角三角形都有一条边与平行，
这5个小直角三角形周长的和等于直角的周长，
故答案为：
【点睛】本题主要考查了平移的应用，正确理解小直角三角形的周长和等于直角的周长是解题的关键．
9．（2022春·山东青岛·七年级统考期中）将棱长为的正方体毛坯，切去一个棱长为的小正方体，得到如图所示的零件，则该零件的表面积是___________．

【答案】54
【分析】根据平移的性质，从正方体毛坯一角挖去一个小正方体得到的零件的表面积等于原正方体表面积．
【详解】解：挖去一个棱长为的小正方体，得到的图形与原图形表面积相等，则表面积是．
故答案为：54．
【点睛】本题考查了整体的思想及简单几何体表面积的计算能力．利用平移的性质是解题的关键．
10．（2022春·吉林长春·九年级校考阶段练习）如图，已知矩形，，，在其矩形内部有三个小矩形，则这三个小矩形的周长之和为______．

【答案】
【分析】根据平移的性质，可知三个矩形的周长等于矩形的周长．
【详解】如图所示：
三个小矩形的周长等于矩形的周长
∴三个小矩形的周长等于
故答案为：．
【点睛】本题考查生活中的平移现象，掌握平移的性质是正确解题的关键．
11．（2022·全国·七年级专题练习）如图，一楼梯的高度为6.4m，水平宽度为8.6m，现要在楼梯的表面铺一种地毯，此种地毯每米需10元钱，那么购买地毯需要______元．

【答案】150
【分析】根据题意，结合图形，先把楼梯的横竖向上向左平移，构成一个矩形，再求得其面积，则购买地毯的钱数可求．
【详解】利用平移线段，把楼梯的横竖向上向左平移，构成一个矩形，长宽分别为6.4米，8.6米
∴地毯的长度为6.4+8.6=15米，



答：购买地毯至少需要150元．
【点睛】本题考查了平移性质，解决此题的关键是要利用平移的知识，把要求的所有线段平移到一条直线上进行计算．
12．（2022秋·浙江温州·七年级校考期中）如图，在一块长，宽的长方形草地上，修建三条宽均为的长方形小路，则这块草地的绿地面积（图中空白部分）为 ___________

【答案】300
【分析】根据平移的性质，可得这块草地的绿地部分是一个长为米，宽为米的长方形，然后进行计算即可解答．
【详解】解：依题意，

．
故答案为：300．
【点睛】本题考查了平移的性质，根据平移的性质求得空白部分的长与宽是解题的关键．
13．（2022秋·湖北随州·七年级校考阶段练习）如图，直角梯形ABCD，ADBC，ABBC，BC＝8，若将此梯形向下平移2个单位，且FC＝1，则图中阴影部分的面积为___________

【答案】15
【分析】先根据平移的性质得出BCMN，BC＝MN＝8，∠M＝∠ABC＝90°，BM＝2，则四边形BMNF是直角梯形，然后根据列式计算即可．
【详解】解：如图，由平移得：BCMN，BC＝MN＝8，∠M＝∠ABC＝90°，BM＝2，
∴四边形BMNF是直角梯形，
∵FC＝1，
∴BF＝8－1＝7，
∴（BF＋MN）·BM＝×（7＋8）×2＝15．
故答案为：15．

【点睛】本题主要考查了平移的性质，仔细观察图形，得到阴影部分的面积等于梯形BMNF的面积是解题的关键．
14．（2022秋·浙江温州·七年级校联考阶段练习）如图，将长为5cm，宽为3cm的长方形ABCD先向右平移2cm，再向下平移1cm，得到长方形，则阴影部分的周长为______cm．

【答案】32
【分析】阴影部分的周长刚好是长方形周长的两倍，据此作答即可．
【详解】∵长方形的长为5cm，宽为3cm，
∴长方形的周长为：5+3+3+5=16（cm），
根据图形可知：阴影部分的周长为：，
即：阴影部分的周长刚好是长方形周长的两倍，
即阴影部分的周长为：16×2=32（cm），
故答案为：32．
【点睛】本题考查了图形的平移的知识，根据图形的平移判断出阴影部分的周长刚好是长方形周长的两倍，是解答本题的关键．
15．（2022秋·甘肃陇南·七年级校考期末）星期天早晨，小刚和爸爸正在商量往楼梯上铺地毯的事，如图所示，

爸爸：“小刚，你帮我算一下，从一层铺到二层需要地毯几米？”
小刚：“我早已用盒尺量好了，每阶高，宽为  …”
爸爸：（打断小刚的话）“不量每阶的高度和宽度，你想想有没有办法？”
小刚：（思索）“有了，只需要量出楼梯的总高和总长度再相加，就行了．”
你认为小刚的方法可以吗？说明理由．
【答案】可以，理由见解析
【分析】根据题意可知地毯的宽度是确定的，求出长即可，再量出楼梯的总高和总长度相加得出答案．
【详解】解：可以，
如图所示：根据图示可得：
地毯的总长度cm=3.15m．

【点睛】本题主要考查了平移的应用，确定地毯的长与楼梯的高和长度的关系是解题的关键．
考点6：与平行线、交线有关的作图问题
典例：（2022秋·浙江金华·七年级统考期末）如图是单位长度为1的网格，△ABC的三个顶点都在格点上，点M也在格点上．只用无刻度直尺在网格内按要求完成作图并回答问题：

(1)过点M作平行于BC的直线l．
(2)将图中△ABC先向左平移2个单位，再向上平移1个单位得到．
①作出平移后的；
②点P是三角形ABC内任意一点，则平移过程中P点经过的路径长为 ．
【答案】(1)见解析
(2)①见解析；②3．
【分析】（1）将点C向右平移两个单位长度得到点N，则过点M、N的直线即为所求作的直线l；
（2）①根据平移的性质作图即可；
②由题意知，平移过程中点P先向左平移2个单位，再向上平移1个单位，即可得P点经过的路径长．
（1）解：如图，直线l即为所求．

（2）①如图，即为所求．

②∵点P是△ABC内任意一点，
∴平移过程中，点P先向左平移2个单位，再向上平移1个单位，
∴P点经过的路径长为2＋1＝3．
故答案为：3．
方法或规律点拨
本题考查作图—平移变换，平移的性质，正确找出对应点的位置是解答本题的关键．
巩固练习
1．（2022秋·山东淄博·六年级统考期末）如图，河道1的一侧有A、B两个村庄，现要铺设一条引水管道把河水引向A、B两村，下列四种方案中最节省材料的是（    ）

A． B． C． D．
【答案】A
【分析】根据垂线段最短以及两点之间线段最短，求解即可．
【详解】解：依据垂线段最短，以及两点之间，线段最短，可得最节省材料的是：

故选：A．
【点睛】本题主要考查了垂线段最短的运用，实际问题中涉及线路最短问题时，其理论依据应从“两点之间，线段最短”和“垂线段最短”这两个中去选择．
2．（2022春·七年级单元测试）如图，汽车站、码头分别位于两点，直线和波浪线分别表示公路与河流．
(1)从汽车站到码头怎样走最近？画出最近路线，并说明理由；
(2)从码头到公路怎样走最近？画出最近路线，并说明理由．

【答案】(1)作图见解析，理由见解析
(2)作图见解析，理由见解析

【分析】（1）根据两点之间线段最短解决问题．
（2）根据垂线段最短解决问题．
【详解】（1）解：如图，连接，线段即为所求作．
（2）如图，过点作于点，线段即为所求作．

【点睛】本题考查作图﹣应用与设计作图，垂线段最短，两点之间线段最短等知识，解题的关键是理解题意，灵活运用所学知识解决问题．
3．（2022春·江苏·七年级期末）如图，线段、点在正方形网格中，所有小正方形的边长都相等．

利用画图工具画图：
(1)①画线段、；
②延长线段到点，使；
③画直线．
利用画图工具比较大小：
(2)线段与线段的大小：______ ；
(3)与的大小______ ．
【答案】(1)见解析
(2)
(3)

【分析】（1）①利用画图工具画图：连接AC、BC即可；
②延长线段AB，截取BD＝AB；
③所作直线经过C、D即可；
（1）量出线段CD与线段CB的长度即可填写；
（2）量出∠CBD与∠A的大小即可填写．
【详解】（1）解：利用画图工具画图：线段、即为所求作的线段，点D为所求作的点，直线CD为所求作的直线，如图所示：

（2）解：线段CD与线段CB的大小关系为：CD＜CB．
故答案为：CD＜CB．
（3）解：∠CBD与∠A的大小为：∠CBD＞∠A．
故答案为：∠CBD＞∠A．
【点睛】本题主要考查了作图−复杂作图，比较线段的长短和角的大小．作两点之间的线段，连接两点即可，由两点作直线，连接两点并向两个方向延长即可得这两点确定的直线．作射线时以一个点为原点，并向另一个方向无限延长．
4．（2022秋·河南信阳·七年级统考期末）按要求画图：

(1)作BEAD交DC于E．
(2)连接AC，作BFAC交DC的延长线于F．
(3)作AG⊥DC于G．
(4)根据图形回答问题：
想要知道点A到点D、点C所在直线的距离，应该测图中哪条线段的长度？为什么？
【答案】(1)见详解
(2)见详解
(3)见详解
(4)AG，理由：点到直线的距离是点到直线的垂线段的长度

【分析】（1）过点B作∠BEC=∠C即可得出答案；
（2）延长DC，作∠BFC=∠ACD即可得出答案；
（3）过点A作AG⊥DC，直接作出垂线即可；
（4）根据点到直线的距离是点到直线的垂线段的长度可知AG为应测线段．
（1）
如图，线段BE即为所求．
；
（2）
如图，线段BF即为所求．
（3）
如图，线段AG即为所求．
（4）
应该测线段AG的长度，
理由：点到直线的距离是点到直线的垂线段的长度．
【点睛】本题考查了基本作图和垂线的性质，根据题意正确的画出线段，掌握点到直线的距离是点到直线的垂线段的长度是解题的关键．
5．（2022春·七年级课时练习）按要求画图：

（1）作 BE∥AD交DC于E．
（2）连接AC，作BF∥AC交DC的延长线于F．
（3）作AG⊥DC于G．
根据图形回答下列问题：
问题1：请用尺子测量点A、点C之间的距离，测量的结果是 cm．（精确到0.1cm．）
问题2：想要知道点A到点D、点C所在直线的距离，应该测图中哪条线段的长度？为什么？
【答案】（1）见解析；（2）见解析；（3）见解析；问题1：3.5；问题2：测图中线段AG的长度，见解析
【分析】（1）如图作图：BE即为所求；
（2）如图作图：BF即为所求；
（3）如图作图：AG即为所求．
问题1：用尺子测量长度；
问题2：根据点到直线的距离定义填写．
【详解】解： （1）如图所示：BE即为所求；
（2）如图所示：BF即为所求；
（3）如图所示：AG即为所求．

问题1：AC=3．5cm ．
问题2：想要知道点A到点D、点C所在直线的距离应该测图中线段AG的长度．
理由是直线外一点到这条直线的垂线段的长度，叫做点到直线的距离．
【点睛】此题考查了直尺作图，解题的关键是熟记点到直线的距离的定义．
6．（2022秋·北京·七年级校考期中）如图，已知三角形，是的平分线，平移三角形，使点移动到点，点的对应点是，点的对应点是．

(1)在图中画出平移后的三角形；
(2)画出点到线段的垂线段；
(3)若，与相交于点，则___________°，___________°．
【答案】(1)见解析
(2)见解析
(3)35°  110°

【分析】（1）根据要求画出图形即可；
（2）根据三角形的高的定义画出图形即可；
（3）利用角平分线的定义，平行线的性质求解即可．
【详解】（1）如图，三角形即为所求；

（2）如图，线段即为所求；
（3）是的平分线，
，
又，
，，
．
故答案为，
【点睛】本题考查平移变换，角平分线的性质，平行线的性质等知识，解题的关键掌握平移变换的性质．
7．（2022·全国·七年级专题练习）画图并填空：
如图，12×10的方格纸，每个小正方形的边长都为1，的顶点都在方格纸的格点上，将按照某方向经过一次平移后得到，图中标出了点C的对应点．

(1)请画出；
(2)连接，，则这两条线段的关系是 ；
(3)利用方格纸，在中画出边上的中线以及边上的高；
(4)线段在平移过程中扫过区域的面积为 ．
【答案】(1)见解析
(2)平行且相等
(3)见解析
(4)20

【分析】（1）利用点C和的位置确定平移的方向与距离，然后利用此平移规律画出A、B的对应点，即可；
（2）根据平移的性质进行判断；
（3）利用网格特点和三角形的中线、高的定义作图；
（4）根据正方形的面积减去两个直角三角形的面积即可得到答案．
【详解】（1）解：如图，为所作；

（2）与的关系是平行且相等；
故答案为：平行且相等
（3）如图，、为所作；
（4）线段在平移过程中扫过区域的面积．
故答案为：20
【点睛】本题考查了作图﹣平移变换：确定平移后图形的基本要素有两个：平移方向、平移距离．作图时要先找到图形的关键点，分别把这几个关键点按照平移的方向和距离确定对应点后，再顺次连接对应点即可得到平移后的图形，还考查了平移的性质、正方形的面积和直角三角形的面积等知识．
8．（2022秋·浙江台州·七年级统考期末）如图，在7×5的方格中，三角形ABC的顶点均在格点上，点D为格点．

(1)在图中作出线段DE（E点在格上），使；
(2)在图中作出线段DF（F点在格上），使．
【答案】(1)见解析
(2)见解析

【分析】（1）根据格点的特点，点B向右平移3格，向上平移4格到达点A，因此将点D向右平移3格，向上平移4格到达格点即为点E，连接DE即可；
（2）将点D向左平移1格，向上平移2格到达格点F，连接DF，作出AC的平行线即可.
（1）
解：线段DF即为所求作的线段，如图所示：

（2）
解：作线段，
∴，
∵，
∴，
∴，
∴线段DF为所求作的线段，如图所示：
或
【点睛】本题主要考查了平移作图，平行线的性质，根据网格的特点作出与已知线段平行的线段，是解题的关键．
9．（2022秋·江苏扬州·七年级校考期中）如图，在方格纸内将△ABC水平向右平移4个单位得到△．

(1)画出△；
(2)利用网格点和直尺画图：画出AB边上的中线CD，请在图中标出点D；
(3)图中△ABC的面积是_________．
【答案】(1)见解析；
(2)见解析；
(3)8

【分析】（1）根据平移的性质即可画出△；
（2）利用网格点即可画出AB边上的中线CD；
（3）根据网格利用割补法即可求出图中△ABC的面积；
（1）
如图，△即为所求；
（2）
如图，中线CD即为所求；

（3）
△ABC的面积=；
故答案为：8；
【点睛】本题考查了作图-平移变换及求三角形的面积，解决本题的关键是掌握平移的性质．
10．（2022秋·河北石家庄·七年级校联考期中）在正方形网格中，每个小正方形的边长均为个单位长度，的三个顶点的位置如图所示，现将平移，点平移到点的位置，、点平移后的对应点分别是、．

(1)画出平移后的；
(2)连接、，则这两条线段之间的位置关系是______．
【答案】(1)见解析
(2)

【分析】（1）利用平移变换的性质分别作出B，C的对应点，即可；
（2）利用平移变换的性质判断即可．
（1）
如图，

即为所求；
（2）
根据平移的性质，可得，
故答案为：．
【点睛】本题考查作图平移变换，解题的关键是掌握平移变换的性质，属于中考常考题型．平移后的图形中的每一点都是由原图形中的某一点移动后得到的，连接各组对应点的线段平行（或在一条直线上）且相等。
考点7：平行线性质与判定的综合问题
典例：（2022秋·湖北宜昌·七年级统考期中）已知BCOA，∠B＝∠OAC＝104°，试回答下列问题：

(1)如图（1），求证：OBAC．
(2)如图（2），若点E，F在BC上，且满足∠FOC＝∠AOC，并且OE平分∠BOF，试求∠EOC的度数．
(3)在图（2）的条件下，若平行移动AC，如图（3），那么∠OCB：∠OFB的值是否会发生变化？若变化，试说明理由；若不变，求出这个比值．
【答案】(1)见解析
(2)38°
(3)∠OCB：∠OFB的值不发生变化，理由见解析，比值为
【分析】（1）由同旁内角互补，两直线平行证明．
（2）由∠FOC=∠AOC，并且OE平分∠BOF得到∠EOC=∠EOF+∠FOC=（∠BOF+∠FOA）=∠BOA，算出结果．
（3）先得出结论：∠OCB：∠OFB的值不发生变化，理由为：由BC与AO平行，得到一对内错角相等，由∠FOC=∠AOC，等量代换得到一对角相等，再利用外角性质等量代换即可得证；
（1）解：∵BCOA，
∴∠B+∠O=180°，
又∵∠B=∠A，
∴∠A+∠O=180°，
∴OBAC；
（2）∵∠B+∠BOA=180°，∠B=104°，
∴∠BOA=76°，
∵OE平分∠BOF，
∴∠BOE=∠EOF，
又∵∠FOC=∠AOC，
∴∠EOF+∠FOC=（∠BOF+∠FOA）=∠BOA=38°；
（3）结论：∠OCB：∠OFB的值不发生变化．理由为：
∵BCOA，
∴∠FCO=∠COA，
又∵∠FOC=∠AOC，
∴∠FOC=∠FCO，
∴∠OFB=∠FOC+∠FCO=2∠OCB，
∴∠OCB：∠OFB=1：2=．
方法或规律点拨
此题考查了平行线的判定与性质，角平分线的定义，以及角的计算，熟练掌握平行线的判定与性质是解本题的关键．
巩固练习
1．（2022·全国·七年级专题练习）已知，的平分线与的平分线相交于点F．

(1)在图1中，求证：
①；
②；
(2)如图2，当，时，请你写出与之间的关系，并加以证明；
(3)当，，且时，请你直接写出的度数（用含m，n的式子表示）
【答案】(1)证明见详解；
(2)，证明见详解；
(3)

【分析】（1）①根据平行线的性质可得：，
②根据平行线的性质可得：，
（2）设，，则，，，根据（1）和四边形内角和得等式可得结论；
（3）同（2）将3倍换为n倍，同理可得结论；
【详解】（1）证明：①如图１，过点作

，
，
，


，

证明：②如图１，过点作


，


，
即
（2）解：关系式为，
证明：设，
，时，且平分，平分，
，

由（１）得，
，
，
，
即，
，

（3）解：设则
，，
由（１）可得
，
，
，
，
，
即的度数（用含m，n的式子表示）表示为
【点睛】本题主要考查了平行线的性质和角平分线、n等分线及四边形的内角和的运用，解决问题的关键是作辅助线构造同旁内角以及内错角，依据平行线的性质进行推导计算，解题时注意类比思想的运用．
2．（2022秋·北京·七年级北京市第一六一中学校考期末）如图1，已知直线与直线交于点E，直线与直线交于点F，平分交直线于点M，且．点G是射线上的一个动点（不与点M、F重合），平分交直线于点H，过点H作交直线于点N，设，．

图1

图2
(1)求证：；
(2)当点G在点F的右侧时，
①依据题意在图1中补全图形；
②若，则α＝　 　度；
(3)当点G在运动过程中，α和β之间有怎样的数量关系？请写出你的猜想，并加以证明．
【答案】(1)见解析
(2)①见解析；②50
(3)或；证明见解析

【分析】（1）根据平分和，可证明，即可解答．
（2）①根据题意画图即可；
②依据平行线的性质可得，再根据平分，，即可得到，再根据三角形内角和定理即可解答；
（3）分两种情况解答：当点G在点F的右侧时，由（2）可得结果；当点G在点F的左侧时，进行解答即可．
【详解】（1）证明：∵平分，
∴，
∵，
∴，
∴；
（2）解：①如图1，

②∵平分，
∴，
∵，
∴，
∵，
∴，
∵

，
∴，
∵，
∴，
解得；
故答案为：50；
（3）解：α和β之间的数量关系为或．
理由如下：
当点G在点F的右侧，由（2）得，
当点G在点F的左侧时，如图2，

∵平分，
∴，
∵，
∴，
∵，
∴

，
∴，
即，
综上所述，α和β之间的数量关系为或．
【点睛】本题考查了平行线的判定与性质，三角形的内角和定理，角平分线的定义，熟练掌握这些知识，并熟练利用角的和差关系进行运算是解题的关键．
3．（2022秋·广东东莞·七年级东莞市光明中学校考期中）阅读下面内容，并解答问题．
已知：如图1，，直线分别交，于点，．的平分线与的平分线交于点．

(1)求证：；
(2)填空，并从下列①、②两题中任选一题说明理由．我选择 　　题．
①在图1的基础上，分别作的平分线与的平分线交于点，得到图2，则的度数为 　　．
②如图3，，直线分别交，于点，．点在直线，之间，且在直线右侧，的平分线与的平分线交于点，则与满足的数量关系为 　　．
【答案】(1)见解析
(2)①；②结论：

【分析】（1）利用平行线的性质解决问题即可；
（2）①利用基本结论求解即可；②利用基本结论，，求解即可．
【详解】（1）证明：如图，过作，
，
，
，

，
平分，平分，
，，
，
在中，，
，
；
（2）解：①如图2中，由题意，，
平分，平分，
，
，
故答案为：；
②结论：．
理由：如图3中，由题意，，，
平分，平分，
，，
，
故答案为：．
【点睛】本题考查平行线的性质和判定，角平分线的性质，垂直的定义，解题的关键是熟练掌握相关的性质．
4．（2022春·陕西汉中·七年级统考期末）解答下列问题
(1)（问题情景）如图1，若，．过点P作，求的度数；
(2)（问题迁移）如图2，，点P在的上方，点E，F分别在，上，连接，，过P点作，问之间有何数量关系？请说明理由；
(3)（联想拓展）如图3所示，在（2）的条件下，已知的平分线和的平分线交于点G，过点G作，用含有的式子表示的度数．

【答案】(1)90°
(2)，理由见解析
(3)

【分析】（1）根据两直线平行内错角相等求出，根据两直线平分线同旁内角互补得到，进而可求出的度数；
（2）首先根据平行线的性质得到，然后根据平行线的性质得到，进而可得到；
（3）首先根据两直线平分线内错角相等得到，然后根据角平分线的概念得到，最后结合（2）的结论求解即可．
【详解】（1）解：，
．
，
，
．
，
．
．
即．
（2）解：．
理由：，
，
，
，
，
，
，
．
（3）解：，
，
，
又的平分线和的平分线交于点G，
，
由（2）可知，，
，
．
【点睛】本题主要考查了平行线的判定和性质，角平分线的概念，熟练掌握平行线的判定和性质是解题的关键．
5．（2022春·四川宜宾·七年级校考阶段练习）问题情境：
在综合实践课上，老师组织七年级（2）班的同学开展了探究两角之间数量关系的数学活动，如图，已知射线，连接，点P是射线上的一个动点（与点A不重合），，分别平分和，分别交射线于点C，D．

探索发现：
“快乐小组”经过探索后发现：
(1)当时，求证：．
(2)不断改变的度数，与却始终存在某种数量关系，
当则_______度，
当时，则_______度，（用含x的代数式表示）
操作探究：
(3)“智慧小组”利用量角器量出和的度数后，探究二者之间的数量关系．他们惊奇地发现，当点P在射线上运动时，无论点P在上的什么位置，与之间的数量关系都保持不变，请写出它们的关系，并说明理由．
【答案】(1)见解析
(2)         
(3)，理由见解析

【分析】（1）根据平行线的性质可求得，再根据角平分线的定义求得即可证得结论；
（2）根据平行线的性质和角平分线的定义推出，进而求解即可；
（3）根据平行线的性质和角平分线的定义得到，，，进而解答即可．
【详解】（1）证明：∵，
∴，
又∵，
∴．
∵，分别平分和，
∴，，
∴，
∴．
（2）解：∵，分别平分和，
∴，，
∴，
∵，
∴，
∴，
∴．
当时，则，
当时，则；
故答案为：，；
（3）解：.理由如下：
∵平分，
∴，
∵，
∴，，
∴．
【点睛】本题考查角平分线的定义、平行线的性质，熟练掌握平行线的性质，能借助图形进行角度运算是解答的关键．
6．（2022·全国·七年级专题练习）已知：直线，点M、N分别在直线、直线上，点E为平面内一点，

(1)如图1，请写出之间的数量关系，并给出证明；
(2)如图2，利用（1）的结论解决问题，若，平分，平分，，求的度数；
(3)如图3，点G为上一点，，， 交于点H，请写出，，之间的数量关系（用含m的式子表示），并给出证明．
【答案】(1)
(2)
(3)
【分析】（1）过点E作，根据题意和平行线的判定得，根据平行线的性质得，，根据，即可得；
（2）根据题意得，，根据平行线的性质得，根据得，即可得，进行计算即可；
（3）根据题意得，，根据得，根据得，根据得，即可得．
【详解】（1），证明如下：
证明：如图1所示，过点E作，

∵，
∴，
∴，，
∵，
∴；
（2）解：∵平分，平分，
∴，，
∵，
∴，
∵，
∴，
∴
=
=
=；
（3），证明如下：
证明：∵，，
∴，，
∵，
∴，
∵
=，
∴，
∵，
∴，
∴．
【点睛】本题考查了平行线的判定与性质，角的和差计算内容，解题的关键是根据图形找到角之间的和差关系．
7．（2022·全国·七年级专题练习）已知，点A在上，的两边与相交于点B，与相交于点C，平分．

(1)如图1，若，，的数量关系为 ；
(2)如图2，在（1）的条件下，若，，求证；
(3)点B、C分别在点D、E的下方，若，，请在备用图中画出相应的图形，并求出的度数．
【答案】(1)
(2)证明见解析
(3)

【分析】（1）由两直线平行内错角相等可得，再根据平分的性质即可推出数量关系；
（2）由得到，再由结合可列出，求得，从而得到，此题得证；
（3）设，根据题意得，，再根据列方程并解出，最后根据余角性质求出，此题得解．
【详解】（1），
证明：∵，平分，
∴，，
∴；
（2）证明：∵，∴，
∵，，，
平分，，
∴，，
∴，
∴与都相交于直线上的A点，
并且在同一平面内，，
∴；
（3）证明：设，则，
，，
，解得
．

【点睛】本题考查了平行线的性质和角平分线的性质的综合题，熟练和灵活运用其性质建立好等量关系是解决本题的关键．
8．（2022·全国·七年级专题练习）如图1，已知直线平行直线，点为直线上一点，点为直线上一点，且，点是直线上一动点，且点在点右侧，过点作交直线于点，连接．

(1)若平分，请直接写出的度数；
(2)作，交直线于点，平分．（说明：解答过程用数字表示角）
①如图2，若点，都在点的右侧，求的度数．
②在点的运动过程中，是否存在这样的情形，使成立？若存在，求出的度数：若不存在，请说明理由．
【答案】(1)
(2)①；②存在，

【分析】（1）先根据平行线的性质求得，再根据角平分线的定义求得结果；
（2）①根据平行线的性质与，角平分线的定义求解便可；
②根据平行线的性质，角的大小关系便可解答．
【详解】（1）解：∵，，
∴，
∵平分，
∴，
∵，
∴．
∴的度数为．
（2）解：①∵平分，
∴，
∵，
∴
∴


．
∴的度数为．
②存在．
当时，
，
∵，
∴，
∴，
∵，
∴．
∴的度数为．
【点睛】本题考查平行线的性质，角平分线的定义．解题的关键是掌握角平分线定义与平行线的性质．
9．（2022春·安徽黄山·八年级校考阶段练习）已知：直线ABCD，直线AD与直线BC交于点E，∠AEC=110°．

(1)如图①，直接写出∠BAD+∠BCD的度数是 ；
(2)①如图①，BF平分∠ABE交AD于点F，DG平分∠CDE交BC于G，求∠AFB+∠CGD的度数；
②如图②，∠ABC=30°，在∠BAE的平分线上取一点P，连接PC，当∠PCD=∠PCB，请直接写出∠APC的度数．（不用写解答过程）
【答案】(1)110°；
(2)①195°；②50°或10°．

【分析】（1）根据平行线的性质和三角形外角的性质即可进行解答；
（2）①过点E作MNAB．利用平行线的判定和性质并结合角平分线的概念分析求解；②分P点在BC的左侧、P在BC的右侧且在CD上方、P在BC的右侧且在CD下方三种情况讨论，结合角度的倍数关系和平行线的性质分析求解．
【详解】（1）解：∵ABCD，
∴∠BAD=∠ADC，
∴，
故答案为：110°；
（2）①过点E作MNAB，

∵ABCD，MNAB，
∴ABMNCD，
∴∠BAE=∠AEM，∠DCE=∠CEM，∠ABE=∠BEN，∠NED=∠EDC，
∵∠AEC=110°，
∴∠BED=110°，
∴∠BAE+∠DCE=∠AEM+∠CEM=∠AEC=110°，
∠ABE+∠CDE=∠BEN+∠NED=∠BED=110°，
∵BF平分∠ABE交AD于F，DG平分∠CDE交BC于G，
∴∠ABF=∠ABE，∠CDG=∠CDE，
∴∠AFB+∠CGD=180°（∠BAE+∠ABF）+180°（∠DCE+∠CDG）
=180°∠BAE-∠ABE+180°∠DCE-∠CDE
=360°（∠BAE+∠DCE）（∠ABE+∠CDE）
=360°110°×110°
=195°，
即∠AFB+∠CGD的度数为195°；
②当点P位于BC左侧时，
此时∠PCD=∠PCB不可能成立，故此情况不存在；
当点P位于BC右侧且位于CD上方时，过点P作PMAB，

∵∠AEC=110°，∠ABC=30°，
∴∠BAE=110°30°=80°，
∵ABCD，MPAB，
∴ABMPCD，
∴∠APM=∠BAP=∠BAE=40°，
∠ABC=∠BCD=30°，
又∵∠PCD=∠PCB，
∴∠PCD=∠BCD=10°，
∴∠MPC=∠PCD=10°，
∴∠APC=∠MPC+∠APM=50°，
当点P位于BC右侧且位于CD下方时，过点P作PMAB，
∵∠AEC=110°，∠ABC=30°，
∴∠BAE=110°30°=80°，
∵ABCD，MPAB，
∴ABMPCD，
∴∠APM=∠BAP=∠BAE=40°，
∠ABC=∠BCD=30°，
又∵∠PCD=∠PCB，
∴∠PCD=∠BCD=30°，
∴∠MPC=∠PCD=30°，
∴∠APC=∠APM∠MPC=10°，
综上，∠APC的度数为50°或10°

【点睛】本题考查平行线的判定和性质、三角形的外角性质、角平分线的定义、对顶角相等等知识，属于中考常考题型，掌握平行线的判定和性质，正确添加辅助线是解题关键．
10．（2022秋·河北邯郸·七年级邯郸市第二十三中学校考期中）在平面直角坐标系中，D（0，﹣3），M（4，﹣3），直角三角形ABC的边与x轴分别相交于O、G两点，与直线DM分别交于E、F点，∠ACB＝90°．

(1)将直角三角形如图1位置摆放，如果∠AOG＝47°，则∠CEF＝____；
(2)将直角三角形ABC如图2位置摆放，N为AC上一点，∠NED+∠CEF＝180°，请写出∠NEF与∠AOG之间的等量关系，并说明理由．
【答案】(1)137°
(2)∠AOG+∠NEF=90°，理由见解析过程

【分析】（1）作CPx轴，利用D、M点的坐标可得到DMx轴，则CPDMx轴，根据平行线的性质有∠AOG=∠1，∠2+∠CEF=180°，然后利用∠1+∠2=90°得到∠AOG+∠180°-∠CEF=90°，可求解；
（2）作CPx轴，则CPDMx轴，根据平行线的性质得∠AOG=∠1，∠2+∠CEF=180°，由于∠NED+∠CEF=180°，所以∠2=∠NED，然后利用∠1+∠2=90°即可得到∠AOG+∠NEF=90°．
（1）
解：如图1，作CPx轴，

∵D（0，-3），M（4，-3），
∴DMx轴，
∴CPDMx轴，
∴∠AOG=∠1，∠2+∠CEF=180°，
∴∠2=180°-∠CEF，
∵∠1+∠2=90°，
∴∠AOG+180°-∠CEF=90°，
∵∠AOG=47°，
∴∠CEF=137°，
故答案为137°；
（2）
∠AOG+∠NEF=90°．理由如下：
作CP∥x轴，如图2，

∵CP∥DM∥x轴，
∴∠AOG=∠1，∠2+∠CEF=180°，
而∠NED+∠CEF=180°，
∴∠2=∠NED，
∵∠1+∠2=90°，
∴∠AOG+∠NEF=90°．
【点睛】本题考查了平行线的判定与性质：平行线于同一条直线的两直线平行；两直线平行，同位角相等；两直线平行，同旁内角互补．
11．（2022秋·上海杨浦·七年级校考期中）已知：直线分别与直线，相交于点，，平分，，，分别为直线和线段上的点．

(1)如图，平分，若，求的度数．
(2)如图，平分交于点，于点，当在直线上运动（不与点重合）时，探究与的关系，并证明你的结论．
【答案】(1)
(2)或，证明见解析

【分析】（1）首先作，根据平行线的性质，推得；然后根据，推得，据此求出的度数即可．
（2）①首先判断出，然后根据，可得，推得，再根据，推得即可．
②首先判断出，然后根据，可得，推得，再根据，推得即可．
（1）
解：如图，作，
，
，，
，，
，，
平分，平分，
，，
，
，
，
，
，
．
（2）
解：①如图，
，
，理由如下：
平分，平分，
，，
，
，
，
，
，
．
②如图，
，
，理由如下：
平分，平分，
，，
，
，
，
，
，
．
综上，可得
当在直线上运动（不与点重合）时，或．
【点睛】此题主要考查了平行线的性质和应用，要熟练掌握，解答此题的关键是要明确：①定理：两条平行线被第三条直线所截，同位角相等．简单说成：两直线平行，同位角相等．②定理：两条平行线被第三条直线所截，同旁内角互补．简单说成：两直线平行，同旁内角互补．③定理：两条平行线被第三条直线所截，内错角相等．简单说成：两直线平行，内错角相等．
12．（2022秋·广东佛山·七年级校考阶段练习）如图，直线，直线和直线分别交于C，D两点，点A，B分别在直线上，点P在直线上，连结．

(1)如图①若点P在线段上，，则的大小为__________度；
(2)如图①若点P在线段上（不与点C，D重合），直接写出之间的数量关系；
(3)如图②若点P在线段的延长线上或在其反向延长线上，写出之间的数量关系；画出图形，并说明理由．
【答案】(1)55
(2)
(3)点P在线段的延长线上时，点P在线段的延长线上时．证明见详解．

【分析】（1）过点P作PG∥l1，通过平行线的性质解题即可．
（2）过点P作PG∥l1，通过平行线的性质解题即可
（3）分当P在DC延长线上时；当P在CD延长线上时，三种情况讨论求解即可．
（1）

解：如图所示，过点P作PG∥l1，
∴∠APG=∠PAC=15°，
∵l1∥l2，
∴PG∥l2，
∴∠BPG=∠PBD=40°，
∴∠APB=∠APG+∠BPG=55°；
（2）
由第一问可知：
∠APG=∠PAC，∠BPG=∠PBD，
∴
（3）

如图1所示，当P在DC延长线上时，过点P作PG∥l1，
∴∠APG=∠PAC，
∵l1∥l2，
∴PG∥l2，
∴∠BPG=∠PBD=40°，
∴∠APB=∠BPG-∠APG=∠PBD-∠PAC；
如图2所示，当P在CD延长线上时，过点P作PG∥l1，
∴∠APG=∠PAC，
∵l1∥l2，
∴PG∥l2，
∴∠BPG=∠PBD，
∴∠APB=∠APG-∠BPG=∠PAC-∠PBD；
∴综上所述，当P在线段CD上时，∠APB=∠PAC +∠PBD；当P在DC延长线上时，∠APB=∠PBD-∠PAC；当P在CD延长线上时，∠APB=∠PAC-∠PBD．
【点睛】本题主要考查平行线的性质及其辅助线的添加方法，能够熟练的添加平行线做为辅助线并运用平行线的性质求角度的关系是解题的关键．
13．（2022秋·浙江宁波·七年级校考期末）【原题】已知直线ABCD，点P为平行线AB，CD之间的一点，如图1，若∠ABP=50°，∠CDP=60°，BE平分∠ABP，DE平分∠CDP．

(1)则∠P=______，∠E=______．
(2)【探究】如图2，当点P在直线AB的上方时，若∠ABP=α，∠CDP=β，∠ABP和∠CDP的平分线交于点，∠ABE1与的角平分线交于点，∠ABE与∠CDE的角平分线交于点，…以此类推，求∠E的度数，并猜想∠E的度数．
(3)【变式】如图3，∠ABP的角平分线的反向延长线和∠CDP的补角的角平分线交于点E，试直接写出∠P与∠E的数量关系．
【答案】(1)110°，55°
(2)∠E的度数为，∠E的度数为
(3)∠DEB=90°-∠P

【分析】（1）过E作EFAB，而ABCD，根据平行线的性质和角平分线的性质即可求解；
（2）根据平行线的性质和角平分线的性质即可求解；
（3）过E作EGAB，而ABCD，根据平行线的性质和角平分线的性质即可求解．
（1）
如图1，过E作EFAB，而ABCD，
∴ABCDEF，
∴∠ABE=∠FEB，∠CDE=∠FED，
∴∠BED=∠BEF+∠DEF=∠ABE+∠CDE，
又∵∠ABP=50°，∠CDP=60°，BE平分∠ABP，DE平分∠CDP，
∴∠ABE=∠ABP=25°，∠CDE=∠CDP=30°，
∴∠BED=25°+30°=55°，
同理：∠BPD=110°．
故答案为：110°，55°；
（2）
如图2，∵∠ABP和∠CDP的平分线交于点，
∴∠ABE=∠ABP=α，∠CDE=∠CDP=，
∵ABCD，
∴∠CDF=∠AFE=，
∴∠E=∠AFE-∠ABE=，
∵∠ABE与∠CDE的角平分线交于点E，
∴∠ABE=∠ABE=，∠CDE=∠CDE=，
∵ABCD，
∴∠CDG=∠AGE=，
∴∠E=∠AGE-∠ABE=，
同理可得，∠E=，
以此类推，∠E的度数为；
（3）
∠DEB=90°-∠P．理由如下：
如图3，过E作EGAB，而ABCD，
∴ABCDEG，
∴∠MBE=∠BEG，∠FDE=∠GED，
∴∠DEB=∠BEG+∠DEG=∠MBE+∠FDE=∠ABQ+∠FDE，
又∵∠ABP的角平分线的反向延长线和∠CDP的补角的角平分线交于点E，
∴∠FDE=∠PDF=(180°-∠CDP)，∠ABQ=∠ABP，
∴∠DEB=∠ABP+(180°-∠CDP)=90°-(∠CDP-∠ABP)，
∵ABCD，
∴∠CDP=∠AHP，
∴∠DEB=90°-(∠CDP-∠ABP)=90°-(∠AHP-∠ABP)=90°-∠P．

【点睛】本题考查了角平分线的性质和平分线的性质，解决本题的关键是掌握以上的性质并熟练的运用．