


青岛市重点中学2022-2023学年数学七年级第二学期期末检测模拟试题含答案
展开青岛市重点中学2022-2023学年数学七年级第二学期期末检测模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。回答非选择题时,将答案写在答题卡上,写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.如图,△ABC是等边三角形,被一平行于BC的矩形所截,AB被截成三等分,则图中阴影部分的面积是△ABC的面积的
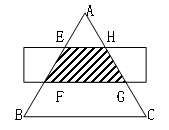
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.某校八年级(2)班第一组女生的体重(单位:![]() ):35,36,36,42,42,42,45,则这组数据的众数为( )
):35,36,36,42,42,42,45,则这组数据的众数为( )
A.45 B.42 C.36 D.35
3.已知 A 和 B 都在同一条数轴上,点 A 表示 2 ,又知点 B 和点 A 相距 5 个单位长度,则点 B 表示的数一定是( )
A.3 B. 7 C.7 或 3 D. 7 或 3
4.若关于x的一元二次方程![]() 有一个根为0,则a的值为( )
有一个根为0,则a的值为( )
A.![]() B.
B.![]() C.
C.![]() D.2
D.2
5.匀速地向如图所示容器内注水,最后将容器注满.在注水过程中,水面高度h随时间t变化情况的大致函数图象(图中OABC为一折线)是( )
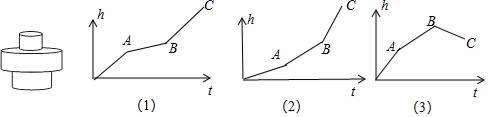
A.(1) B.(2) C.(3) D.无法确定
6.如图,有两颗树,一颗高10米,另一颗高4米,两树相距8米.一只鸟从一颗树的树梢飞到另一颗树的树梢,问小鸟至少飞行

A.8米 B.10米 C.12米 D.14米
7.函数![]()
![]() 的图象可能是( )
的图象可能是( )
A.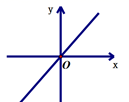 B.
B.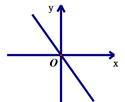
C.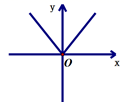 D.
D.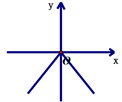
8.为了解2019年泰兴市八年级学生的视力情况,从中随机调查了500名学生的视力情况.下列说法正确的是( )
A.2016年泰兴市八年级学生是总体 B.每一名八年级学生是个体
C.500名八年级学生是总体的一个样本 D.样本容量是500
9.在平面直角坐标系中,点M(3,2)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
10.如图,在![]() 中,
中,![]() 于点
于点![]() ,
,![]() ,则
,则![]() 的度数是( )
的度数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11.我市某一周每天的最高气温统计如下(单位:℃):27,28,1,28,1,30,1.这组数据的众数与中位数分别是( ).
A.28,28 B.28,1 C.1,28 D.1,1
12.如图,一次函数![]() 和反比例函数
和反比例函数![]() 的图象交于
的图象交于![]() ,
,![]() ,两点,若
,两点,若![]() ,则
,则![]() 的取值范围是( )
的取值范围是( )
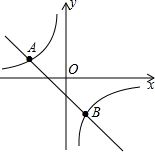
A.![]() B.
B.![]() 或
或![]()
C.![]() D.
D.![]() 或
或![]()
二、填空题(每题4分,满分20分,将答案填在答题纸上)
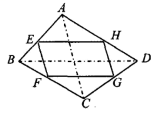
13.如图,四边形 ABCD 中,E、F、G、H 分别为各边的中点,顺次连 结 E、F、G、H,把四边形 EFGH 称为中点四边形.连结 AC、BD,容易证明:中点 四边形 EFGH 一定是平行四边形.
(1)如果改变原四边形 ABCD 的形状,那么中点四边形的形状也随之改变,通过探索 可以发现:当四边形 AB CD 的对角线满足 AC=BD 时,四边形 EFGH 为菱形;当四边形ABCD 的对角线满足 时,四边形 EFGH 为矩形;当四边形 ABCD 的对角线满足 时,四边形 EFGH 为正方形.
(2)试证明:S△AEH+S△CFG= ![]() S□ ABCD
S□ ABCD
(3)利用(2)的结论计算:如果四边形 ABCD 的面积为 2012, 那么中点四边形 EFGH 的面积是 (直接将结果填在 横线上)
14.为了解当地气温变化情况,某研究小组记录了寒假期间连续6天的最高气温,结果如下(单位:℃):-6,-3,x,2,-1,3,若这组数据的中位数是-1,在下列结论中:①方差是8;②极差是9;③众数是-1;④平均数是-1,其中正确的序号是________.
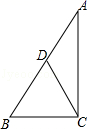
15.如图,Rt△ABC中,∠ACB=90°,AB=6,D是AB的中点,则CD=_____.
16.设甲组数:1,1,2,5的方差为S甲2,乙组数是:6,6,6,6的方差为S乙2,则S甲2与S乙2的大小关系是S甲2_____S乙2(选择“>”、“<”或“=”填空).
17.若二次根式![]() 有意义,则x的取值范围是________.
有意义,则x的取值范围是________.
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18.(5分)2013年1月1日新交通法规开始实施.为了解某社区居民遵守交通法规情况,小明随机选取部分居民就“行人闯红灯现象”进行问卷调查,调查分为“A:从不闯红灯;B:偶尔闯红灯;C:经常闯红灯;D:其他”四种情况,并根据调查结果绘制出部分条形统计图(如图1)和部分扇形统计图(如图2).请根据图中信息,解答下列问题:
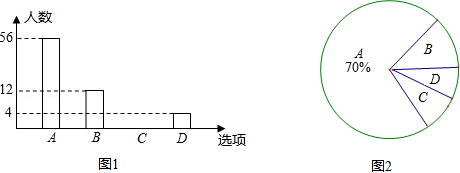
(1)本次调查共选取 名居民;
(2)求出扇形统计图中“C”所对扇形的圆心角的度数,并将条形统计图补充完整;
(3)如果该社区共有居民1600人,估计有多少人从不闯红灯?
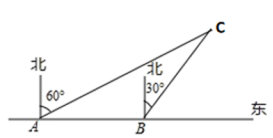
19.(5分)为了维护国家主权和海洋权力,海监部门对我国领海实行常态化巡航管理,如图,正在执行巡航任务的海监船以每小时30海里的速度向正东方航行,在![]() 处测得灯塔
处测得灯塔![]() 在北偏东60°方向上, 继续航行
在北偏东60°方向上, 继续航行![]() 后到达
后到达![]() 处, 此时测得灯塔
处, 此时测得灯塔![]() 在北偏东30°方向上.
在北偏东30°方向上.
(1) 求![]() 的度数;
的度数;
(2)已知在灯塔![]() 的周围15海里内有暗礁,问海监船继续向正东方向航行是否安全?
的周围15海里内有暗礁,问海监船继续向正东方向航行是否安全?
20.(8分)已知x=2+![]() ,求代数式
,求代数式![]() 的值.
的值.
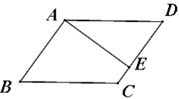
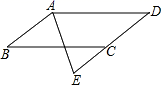
21.(10分)如图,四边形ABCD是平行四边形,AE平分∠BAD,交DC的延长线于点E.求证:DA=DE.
22.(10分)先因式分解,再求值:4x3y﹣9xy3,其中x=﹣1,y=1.
23.(12分)在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 的中点,点
的中点,点![]() 是射线
是射线![]() 上一点,
上一点,![]() 于点
于点![]() ,且
,且![]() ,连接
,连接![]() ,作
,作![]() 于点
于点![]() ,交直线
,交直线![]() 于点
于点![]() .
.
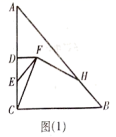
(1)如图(1),当点![]() 在线段
在线段![]() 上时,判断
上时,判断![]() 和
和![]() 的数量关系,并加以证明;
的数量关系,并加以证明;
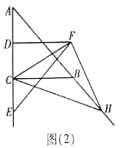
(2)如图(2),当点![]() 在线段
在线段![]() 的延长线上时,问题(1)中的结论是否依然成立?如果成立,请求出当
的延长线上时,问题(1)中的结论是否依然成立?如果成立,请求出当![]() 和
和![]() 面积相等时,点
面积相等时,点![]() 与点
与点![]() 之间的距离;如果不成立,请说明理由.
之间的距离;如果不成立,请说明理由.
参考答案
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1、C
2、B
3、D
4、C
5、A
6、B
7、C
8、D
9、A
10、B
11、D
12、D
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13、![]() ;(2)详见解析;(3)1
;(2)详见解析;(3)1
14、②③④
15、1
16、>
17、![]()
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18、(1)80人;(2)见解析;(3)1120人.
19、(1)30°;(2)海监船继续向正东方向航行没有触礁的危险,见解析
20、![]()
21、证明见解析.
22、2.
23、(1)![]() ,证明见解析;(2)依然成立,点
,证明见解析;(2)依然成立,点![]() 与点
与点![]() 之间的距离为
之间的距离为![]() .理由见解析.
.理由见解析.
绍兴市重点中学2022-2023学年数学七年级第二学期期末质量检测模拟试题含答案: 这是一份绍兴市重点中学2022-2023学年数学七年级第二学期期末质量检测模拟试题含答案,共7页。试卷主要包含了考生要认真填写考场号和座位序号,函数的自变量的取值范围是,点关于原点对称点的坐标是,下列运算正确的是等内容,欢迎下载使用。
荆门市重点中学2022-2023学年七年级数学第二学期期末达标检测模拟试题含答案: 这是一份荆门市重点中学2022-2023学年七年级数学第二学期期末达标检测模拟试题含答案,共7页。试卷主要包含了考生要认真填写考场号和座位序号,一组数据等内容,欢迎下载使用。
包头市重点中学2022-2023学年数学七年级第二学期期末检测模拟试题含答案: 这是一份包头市重点中学2022-2023学年数学七年级第二学期期末检测模拟试题含答案,共8页。












