湘教版八年级下册2.6.2菱形的判定课时作业

[菱形的判定]

一、选择题

1.(2020南通)下列条件中,能判定▱ABCD是菱形的是 (　　)

A.AC=BD B.AB⊥BC C.AD=BD D.AC⊥BD

2.如图,已知△ABC,AB=AC,将△ABC沿边BC折叠,得到△DBC,其与原△ABC拼成四边形ABDC,则能直接判定四边形ABDC是菱形的依据是              (　　)

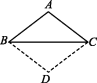
A.一组邻边相等的平行四边形是菱形 

B.四条边都相等的四边形是菱形 

C.对角线互相垂直的平行四边形是菱形 

D.对角线互相垂直平分的四边形是菱形

3.如图,在四边形ABCD中,对角线AC,BD相交于点O,AO=CO,BO=DO.添加下列条件,不能判定四边形ABCD是菱形的是              (　　)

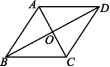
A.AB=AD B.AC=BD C.AC⊥BD D.∠ABO=∠CBO

4.如图,四边形ABCD的四边相等,且面积为120 cm2,对角线AC=24 cm,则四边形ABCD的周长为              (　　)

A.52 cm B.40 cm C.39 cm D.26 cm

5.如图,在菱形ABCD中,E,F,G,H分别是菱形四边的中点,连接EG与FH交于点O,则图中共有菱形              (　　)

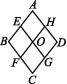
A.4个　 B.5个　 C.6个　 D.7个

二、填空题

6.(2020嘉兴)如图,▱ABCD的对角线AC,BD相交于点O,请添加一个条件:　　　　　　　　　　,使▱ABCD是菱形. 

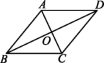
7.如图,在△ABC中,D是BC的中点,点E,F分别在线段AD及其延长线上,且DE=DF,给出下列条件:①BE⊥EC;②BF∥EC;③AB=AC.从中选择一个条件使四边形BECF是菱形,你认为这个条件是　　　　　(只填写序号).               

三、解答题

8.(2020恩施州)如图,AE∥BF,BD平分∠ABC交AE于点D,点C在BF上且BC=AB,连接CD.

求证:四边形ABCD是菱形.

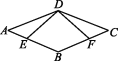
9.如图,已知四边形ABCD是平行四边形,E,F分别是AB,BC上的点,AE=CF,且∠AED=∠CFD.求证:

(1)△AED≌△CFD;

(2)四边形ABCD是菱形.

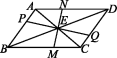
10.(2020滨州)如图,过▱ABCD对角线AC与BD的交点E作两条互相垂直的直线,分别交边AB,BC,CD,DA于点P,M,Q,N.

(1)求证:△PBE≌△QDE;

(2)顺次连接点P,M,Q,N,求证:四边形PMQN是菱形.

图   

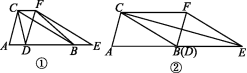
 [图形变换] 两个全等的三角形ABC和DEF重叠在一起,△ABC的面积为3,且AB=CB,固定△ABC不动,将△DEF进行如下操作:

(1)如图①,△DEF沿线段AB向右平移(点D在线段AB上移动),连接DC,CF,FB,四边形CDBF的形状在不断地变化,但它的面积不变,请求出其面积;

(2)如图②,当点D向右平移到点B时,连接CF,CE,试判断CE与BF的位置关系,并说明理由;

(3)在(2)的条件下,若∠AEC=15°,求AB的长.

答案

1.D

2. B　∵将△ABC沿边BC折叠得到△DBC,∴AB=BD,AC=CD.又∵AB=AC,∴AB=BD=CD=AC,∴四边形ABDC是菱形.故选B.

3. B　∵AO=CO,BO=DO,

∴四边形ABCD是平行四边形.

若AB=AD或AC⊥BD,均可判定四边形ABCD是菱形;

若∠ABO=∠CBO,由AD∥BC知∠CBO=∠ADO,∴∠ABO=∠ADO,

∴AB=AD,∴四边形ABCD是菱形;

若AC=BD,可判定四边形ABCD是矩形,但不能判定四边形ABCD是菱形.

4. A　连接BD.∵四边形ABCD的四边相等,∴四边形ABCD为菱形.

∵它的面积为120 cm2,对角线AC=24 cm,

∴120=×24BD,∴BD=10 cm,

∴AB==13(cm),

∴四边形ABCD的周长为4×13=52(cm).

故选A.

5. B　∵四边形ABCD是菱形,E,F,G,H分别是菱形四边的中点,

∴AE=AH=HD=GD=CG=CF=FB=BE=OE=OG=OH=OF,

∴四边形AEOH,HOGD,EOFB,OFCG和ABCD均为菱形,共5个.

6. AB=BC(答案不唯一)

 本题四边形ABCD已经是平行四边形,故只需邻边相等即可,所以填AB=BC.

7. ③

 需添加条件③.理由:∵D是BC的中点,∴BD=CD.又∵DE=DF,∴四边形BECF为平行四边形.∵AB=AC,D是BC的中点, ∴AD⊥BC,∴▱BECF为菱形.故答案为③.

8.证明:∵AE∥BF,∴∠ADB=∠DBC.

∵BD平分∠ABC,∴∠DBC=∠ABD,

∴∠ADB=∠ABD,∴AB=AD.

又∵AB=BC,∴AD=BC.

又∵AE∥BF,即AD∥BC,

∴四边形ABCD是平行四边形.

又∵AB=AD,∴四边形ABCD是菱形.

9.证明:(1)∵四边形ABCD是平行四边形,

∴∠A=∠C.

在△AED与△CFD中,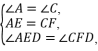

∴△AED≌△CFD(ASA).

(2)由(1)知,△AED≌△CFD,∴AD=CD.

又∵四边形ABCD是平行四边形,

∴四边形ABCD是菱形.

10.证明:(1)∵四边形ABCD是平行四边形,

∴EB=ED,AB∥CD,

∴∠EBP=∠EDQ.

在△PBE和△QDE中,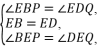

∴△PBE≌△QDE(ASA).

(2)如图所示:

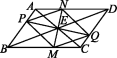
∵△PBE≌△QDE,∴EP=EQ.

同(1)可证△BME≌△DNE,

∴EM=EN,∴四边形PMQN是平行四边形.

又∵PQ⊥MN,∴四边形PMQN是菱形.

[素养提升]

解:(1)如图①,过点C作CH⊥AB于点H.

由平移的性质可得CF=AD,CF∥AB,

∴S四边形CDBF=(CF+BD)·CH=(AD+BD)·CH=AB·CH.

∵S△ABC=AB·CH=3,

∴S四边形CDBF=3.

(2)CE⊥BF.

理由:由平移的性质可得BE=CF,BE∥CF,

∴四边形CBEF是平行四边形.

∵AB=CB,AB=BE,∴CB=BE,

∴四边形CBEF是菱形,

∴CE⊥BF.

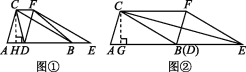
(3)如图②,过点C作CG⊥AB于点G.

∵CB=BE,∠AEC=15°,

∴∠BCE=∠AEC=15°,

∴∠ABC=∠AEC+∠BCE=30°,

∴在Rt△BCG中,CG=CB.

∵AB=CB,

∴CG=AB,

∴S△ABC=AB·CG=AB2=3,

∴AB=2(负值已舍去).