湘教版八年级下册4.4 用待定系数法确定一次函数表达式当堂检测题

[用待定系数法确定一次函数表达式]

一、选择题

1.一个正比例函数的图象经过点(2,-1),则它的表达式为 (　　)

A.y=-2x B.y=2x C.y=-x D.y=x

2.图中的直线对应的函数表达式是 (　　)

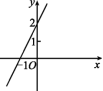
A.y=2x+2 B.y=-2x-2 C.y=-2x+2 D.y=2x-2

3.已知y-3与x成正比例,且当x=2时,y=7,则y与x之间的函数表达式为 (　　)

A.y=2x+3 B.y=2x-3 C.y-3=2x+3 D.y=3x-3

4.如图,把直线y=-2x向上平移后得到直线AB,直线AB经过点(a,b),且2a+b=6,则直线AB的表达式是              (　　)

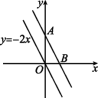
A.y=-2x-3　　 B.y=-2x-6　 C.y=-2x+3　 D.y=-2x+6

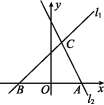
5.如图,已知直线l1:y=-2x+4与x轴,y轴分别交于A,B两点,那么过原点O且将△AOB的面积平分的直线l2的表达式为              (　　)

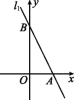
A.y=x B.y=x C.y=x D.y=2x

二、填空题

6.(2020郴州)小红在练习仰卧起坐,本月1日至4日的成绩与日期具有如下关系:

小红的仰卧起坐成绩y与日期x之间近似为一次函数关系,则该函数的表达式为　　　　. 

7.(2020黔西南州)如图,正比例函数的图象与一次函数y=-x+1的图象相交于点P,点P到x轴的距离是2,则这个正比例函数的表达式是　　　　. 

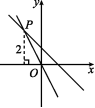
8.(2020南京)将一次函数y=-2x+4的图象绕原点O逆时针旋转90°,所得到的图象对应的函数表达式是　　　　. 

9.已知y是x的一次函数,当-2≤x≤2时,-1≤y≤3,那么这个函数的表达式是　　　　　　　　. 

三、解答题

10.已知一次函数的图象经过点(3,5)和(-4,-9).

(1)求这个一次函数的表达式;

(2)求这个函数的图象与x轴的交点坐标.

11.已知y与x+3成正比例,且当x=1时,y=8.

(1)求y与x之间的函数表达式;

(2)若点(a,6)在这个函数的图象上,求a的值.

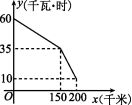
12.图是某型号新能源纯电动汽车充满电后,蓄电池剩余电量y(千瓦·时)关于已行驶路程x(千米)的函数图象.

(1)根据图象,直接写出蓄电池剩余电量为35千瓦·时时汽车已行驶的路程,当0≤x≤150时,求1千瓦·时的电量汽车能行驶的路程;

(2)当150≤x≤200时,求y关于x的函数表达式,并计算当汽车已行驶180千米时,蓄电池的剩余电量.

图   

13.(2020南通)如图,直线l1:y=x+3与过点A(3,0)的直线l2交于点C(1,m),与x轴交于点B.

(1)求直线l2的表达式;

(2)点M在直线l1上,MN∥y轴,交直线l2于点N.若MN=AB,求点M的坐标.

图 

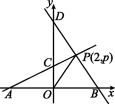
 [转化思想] 如图,A,B分别是x轴上位于原点左、右两侧的点,点P(2,p)在第一象限,直线PA交y轴于点C(0,2),直线PB交y轴于点D,此时S△AOP=6.

(1)求p的值;

(2)若S△BOP=S△DOP,求直线BD的函数表达式.

答案

1. C　设该正比例函数的表达式为y=kx.∵正比例函数的图象经过点(2,-1),∴-1=2k,解得k=-,∴这个正比例函数的表达式是y=-x.

2.A

3.A

4. D　∵直线AB经过点(a,b),且2a+b=6,∴直线AB经过点(a,6-2a).∵直线AB与直线y=-2x平行,∴设直线AB的表达式是y=-2x+b1.把点(a,6-2a)代入函数表达式,得6-2a=-2a+b1,则b1=6,∴直线AB的表达式是y=-2x+6.

5. D　当y=0时,-2x+4=0,解得x=2,则A(2,0);

当x=0时,y=-2x+4=4,则B(0,4),

∴线段AB的中点坐标为(1,2).

∵直线l2把△AOB的面积平分,

∴直线l2经过AB的中点.

设直线l2的表达式为y=kx.

把(1,2)代入,得2=k,即k=2,

∴直线l2的表达式为y=2x.

6. y=3x+37

 设该函数的表达式为y=kx+b.

根据题意,得解得

∴该函数的表达式为y=3x+37.

故答案为y=3x+37.

7. y=-2x

 ∵点P到x轴的距离为2,∴点P的纵坐标为2.∵点P在一次函数y=-x+1的图象上,∴2=-x+1,解得x=-1,∴点P的坐标为(-1,2).设正比例函数的表达式为y=kx.把P(-1,2)代入,得2=-k,解得k=-2,∴正比例函数的表达式为y=-2x,因此本题答案为y=-2x.

8. y=x+2

 直线y=-2x+4与x轴,y轴的交点坐标分别为(2,0),(0,4),该两点逆时针旋转90°后的对应点分别是(0,2),(-4,0).

设旋转后的直线的表达式为y=kx+b.

把点(0,2),(-4,0)代入,得

解得

故旋转后的直线的表达式为y=x+2.

9. y=x+1或y=-x+1

 设所求的函数表达式为y=kx+b(k,b为常数,k≠0).

分情况讨论:

(1)当k>0时,函数图象经过点(-2,-1),(2,3),则解得则函数的表达式是y=x+1;

(2)当k<0时,函数图象过点(-2,3),(2,-1),则解得则函数的表达式是y=-x+1.

故这个函数的表达式是y=x+1或y=-x+1.

10.解:(1)设一次函数的表达式为y=kx+b,则解得

所以这个一次函数的表达式为y=2x-1.

(2)令y=0,得2x-1=0,解得x=,

故这个函数的图象与x轴的交点坐标为,0.

11.解:(1)根据题意,设y=k(x+3).

把x=1,y=8代入y=k(x+3),得8=4k,

解得k=2.

则y与x之间的函数表达式为y=2(x+3)=2x+6.

(2)把点(a,6)代入y=2x+6,得6=2a+6,

解得a=0.

12.解:(1)由图象可知,蓄电池剩余电量为35千瓦·时时汽车已行驶的路程为150千米.

当0≤x≤150时,1千瓦·时的电量汽车能行驶的路程为=6(千米).

(2)当150≤x≤200时,设y关于x的函数表达式为y=kx+b.把点(150,35),(200,10)代入,得解得

∴当150≤x≤200时,y关于x的函数表达式为y=-0.5x+110.

当x=180时,y=-0.5×180+110=20.

故当150≤x≤200时,y关于x的函数表达式为y=-0.5x+110,当汽车已行驶180千米时,蓄电池的剩余电量为20千瓦·时.

13.解:(1)把x=1代入y=x+3,得y=4,∴C(1,4).

设直线l2的表达式为y=kx+b.

把点(1,4)(3,0)代入,得

解得∴y=-2x+6.

(2)在y=x+3中,令y=0,得x=-3,

∴B(-3,0),则AB=3-(-3)=6.

设M(a,a+3).

由MN∥y轴,点N在直线l2上,得N(a,-2a+6),

∴MN=|a+3-(-2a+6)|=AB=6,

解得a=3或a=-1,∴M(3,6)或M(-1,2).

[素养提升]

解:如图,过点P作PF⊥y轴于点F,

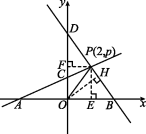
则PF=2.

(1)∵C(0,2),

∴CO=2,

∴S△COP=CO·PF=×2×2=2.

∵S△AOP=6,S△COP=2,∴S△COA=4,

即OA×2=4,∴OA=4.

又∵A是x轴上位于原点左侧的点,

∴A(-4,0).

∵点P(2,p)在第一象限,∴p>0,

∴S△AOP=×4×p=6,∴p=3.

(2)如图,过点P作PE⊥x轴于点E,过点O作OH⊥BD于点H,则OH为△BOP,△DOP的高.

∵S△BOP=S△DOP,且这两个三角形同高,

∴DP=BP,

即P为BD的中点.

∵PF⊥y轴,PE⊥x轴,x轴⊥y轴,

∴PF∥OB,PE∥OD,

∴OB=2PF=4,OD=2PE=6,

∴B(4,0),D(0,6).

设直线BD的函数表达式为y=kx+b,

则解得

∴直线BD的函数表达式为y=-x+6.