


重庆巴蜀常春藤2022-2023学年七下数学期末考试模拟试题含答案
展开重庆巴蜀常春藤2022-2023学年七下数学期末考试模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
考生请注意:
1.答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内,不得在试卷上作任何标记。
2.第一部分选择题每小题选出答案后,需将答案写在试卷指定的括号内,第二部分非选择题答案写在试卷题目指定的位置上。
3.考生必须保证答题卡的整洁。考试结束后,请将本试卷和答题卡一并交回。
一、选择题(每小题3分,共30分)
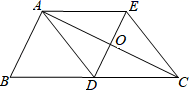
1.如图,在![]() 中,
中,![]() ,若有一动点
,若有一动点![]() 从
从![]() 出发,沿
出发,沿![]() 匀速运动,则
匀速运动,则![]() 的长度
的长度![]() 与时间
与时间![]() 之间的关系用图像表示大致是()
之间的关系用图像表示大致是()
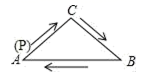
A.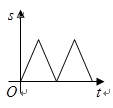 B.
B.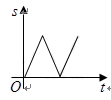
C.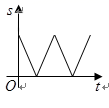 D.
D.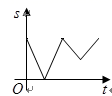
2.某体育馆准备重新铺设地面,已有一部分正三角形的地砖,现要购买另一种不同形状的正多边形地砖与正三角形在同一顶点处作平面镶嵌(正多边形的边长相等),则该体育馆不应该购买的地砖形状是( )
A.正方形 B.正六边形 C.正八边形 D.正十二边形
3.一次函数![]() 与
与![]() 的图象如图所示,则下列结论:①k<0;②a<0,b<0;③当x=3时,y1=y2;④不等式
的图象如图所示,则下列结论:①k<0;②a<0,b<0;③当x=3时,y1=y2;④不等式![]() 的解集是x<3,其中正确的结论个数是( )
的解集是x<3,其中正确的结论个数是( )
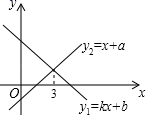
A.0 B.1 C.2 D.3
4.一次函数 y 2x 2 的大致图象是( )
A.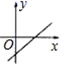 B.
B.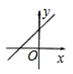 C.
C.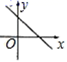 D.
D.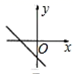
5.如图,在平面直角坐标系中,点A是反函数![]() 图像上的点,过点A与x轴垂直的直线交x轴于点B,连结AO,若
图像上的点,过点A与x轴垂直的直线交x轴于点B,连结AO,若![]() 的面积为3,则k的值为( )
的面积为3,则k的值为( )
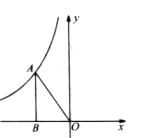
A.3 B.-3
C.6 D.-6
6.在平行四边形ABCD中,∠BAD=110°,∠ABD=30°,则∠CBD度数为( )
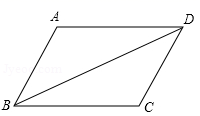
A.30° B.40° C.70° D.50°
7.如图所示,矩形ABCD中,点E在DC上且DE:EC=2:3,连接BE交对角线AC于点O.延长AD交BE的延长线于点F,则△AOF与△BOC的面积之比为( )
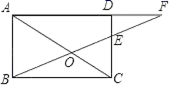
A.9:4 B.3:2 C.25:9 D.16:9
8.已知反比例函数的图象过点M(-1,2),则此反比例函数的表达式为( )
A.y=![]() B.y=-
B.y=-![]() C.y=
C.y=![]() D.y=-
D.y=-![]()
9.在□ABCD中,对角线 AC与 BD 相交于点O , AC10, BD 6,则下列线段不可能是□ABCD 的边长的是( )
A.5 B.6 C.7 D.8
10.下列函数中,一次函数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题(本大题共有6小题,每小题3分,共18分)
11.若![]() 有意义,则x的取值范围是____.
有意义,则x的取值范围是____.
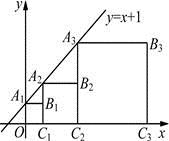
12.正方形![]() ,
,![]() ,
,![]() ,…按如图所示的方式放置.点
,…按如图所示的方式放置.点![]() ,
,![]() ,
,![]() ,…和点
,…和点![]() ,
,![]() ,
,![]() ,…分别在直线
,…分别在直线![]() 和
和![]() 轴上,则点
轴上,则点![]() 的坐标是 .
的坐标是 .
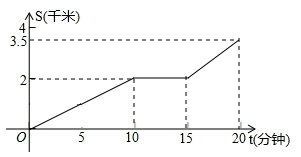
13.一天,小明放学骑车从学校出发路过新华书店买了一本课外书再骑车回家,他所行驶的路程s与时间t的关系如图,则经18分钟后,小明离家还有____千米.
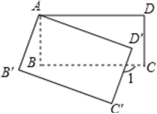
14.如图,将长方形ABCD绕点A顺时针旋转到长方形AB′C′D′的位置,旋转角为α(0°<α<90°),若∠1=125°,则∠α的大小是_______度.
15.某市出租车的收费标准如下:起步价5元,即![]() 千米以内(含
千米以内(含![]() 千米)收费
千米)收费![]() 元,超过
元,超过![]() 千米的部分,每千米收费
千米的部分,每千米收费![]() 元.(不足
元.(不足![]() 千米按
千米按![]() 千米计算)求车费
千米计算)求车费![]() (元)与行程
(元)与行程![]() (千米)的关系式________.
(千米)的关系式________.
16.计算(4![]() +
+![]() )÷3
)÷3![]() 的结果是_____.
的结果是_____.
三、解下列各题(本大题共8小题,共72分)
17.(8分)如图,已知△ABC中,AD是边BC上的中线,过点A作AE∥BC,过点D作DE∥AB,DE与AC、AE分别交于点O、点E,联结EC.
(1)求证:四边形ADCE是平行四边形;
(2)当∠BAC=90°时,求证:四边形ADCE是菱形.
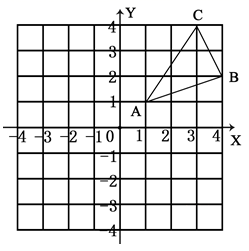
18.(8分)如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
(1) 请画出△ABC向左平移5个单位长度后得到的△A![]() B
B![]() C
C![]() ;
;
(2) 请画出△ABC关于原点对称的△A![]() B
B![]() C
C![]() ;
;
(3) 在![]() 轴上求作一点P,使△PAB的周长最小,请画出△PAB,并直接写出P的坐标.
轴上求作一点P,使△PAB的周长最小,请画出△PAB,并直接写出P的坐标.
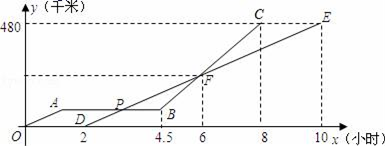
19.(8分)甲、乙两辆汽车沿同一路线赶赴距出发地480千米的目的地,乙车比甲车晚出发2小时(从甲车出发时开始计时),图中折线OABC、线段DE分别表示甲、乙两车所行路程y(千米)与时间x(小时)之间的函数关系对应的图像线段AB表示甲出发不足2小时因故停车检修),请根据图像所提供的信息,解决如下问题:
(1)求乙车所行路程y与时间x的函数关系式;
(2)求两车在途中第二次相遇时,它们距出发地的路程;
(3)乙车出发多长时间,两车在途中第一次相遇?(写出解题过程)
20.(8分)某青春党支部在精准扶贫活动中,给结对帮扶的贫困家庭赠送甲、乙两种树苗让其栽种.已知乙种树苗的价格比甲种树苗贵10元,用480元购买乙种树苗的棵数恰好与用360元购买甲种树苗的棵数相同.
(1)求甲、乙两种树苗每棵的价格各是多少元?
(2)在实际帮扶中,他们决定再次购买甲、乙两种树苗共50棵,此时,甲种树苗的售价比第一次购买时降低了10%,乙种树苗的售价不变,如果再次购买两种树苗的总费用不超过1500元,那么他们最多可购买多少棵乙种树苗?
21.(8分)请把下列证明过程补充完整:
已知:如图,DE∥BC,BE平分∠ABC.求证:∠1=∠1.
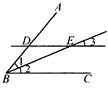
证明:因为BE平分∠ABC(已知),
所以∠1=______ ( ).
又因为DE∥BC(已知),
所以∠2=_____( ).
所以∠1=∠1( ).
22.(10分)如图,在△ABC中,D、E分别是AB、AC的中点,过点E作EF∥AB,交BC于点F.
(1)求证:四边形DBFE是平行四边形;
(2)当△ABC满足什么条件时,四边形DBEF是菱形;为什么.
23.(10分)某校开展“涌读诗词经典,弘扬传统文化”诗词诵读活动,为了解八年级学生在这次活动中的诗词诵背情况,随机抽取了30名八年级学生,调查“一周诗词诵背数量”,调查结果如下表所示:
一周诗词诵背数量(首) |
|
|
|
|
|
|
人数(人) |
|
|
|
|
|
|
(1)计算这![]() 人平均每人一周诵背诗词多少首;
人平均每人一周诵背诗词多少首;
(2)该校八年级共有6![]() 名学生参加了这次活动,在这次活动中,估计八年级学生中一周诵背诗词
名学生参加了这次活动,在这次活动中,估计八年级学生中一周诵背诗词![]() 首以上(含6首)的学生有多少人.
首以上(含6首)的学生有多少人.
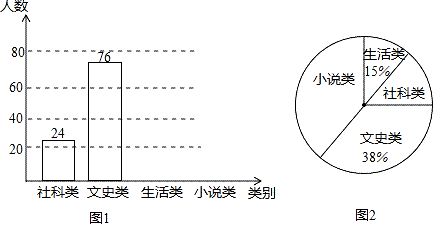
24.(12分)央视热播节目“朗读者”激发了学生的阅读兴趣.某校为满足学生的阅读需求,欲购进一批学生喜欢的图书,学校组织学生会成员随机抽取部分学生进行问卷调查,被调查学生须从“文史类、社科类、小说类、生活类”中选择自己喜欢的一类,根据调查结果绘制了统计图(未完成),请根据图中信息,解答下列问题:
(1)此次共调查了 名学生;
(2)将条形统计图补充完整;
(3)图2中“小说类”所在扇形的圆心角为 度;
(4)若该校共有学生2500人,估计该校喜欢“社科类”书籍的学生人数.
参考答案
一、选择题(每小题3分,共30分)
1、D
2、C
3、D
4、A
5、D
6、B
7、C
8、B
9、D
10、A
二、填空题(本大题共有6小题,每小题3分,共18分)
11、x≥1.
12、(63,32).
13、0.1
14、35.
15、![]()
16、2
三、解下列各题(本大题共8小题,共72分)
17、(1)见解析;(2)四边形ADCE是菱形,见解析.
18、(1)图形见解析;
(2)图形见解析;
(3)图形见解析,点P的坐标为:(2,0)
19、(1)y=1x﹣120;(2)两车在途中第二次相遇时它们距出发地的路程为240千米;
(3)乙车出发1小时,两车在途中第一次相遇.
20、(1)甲种树苗每棵的价格是30元,乙种树苗每棵的价格是40元;(2)他们最多可购买11棵乙种树苗.
21、∠2;角平分线的定义;∠1;两直线平行,同位角相等;等量代换.
22、(1)证明见解析;(2)当AB=BC时,四边形DBEF是菱形,理由见解析.
23、(1)5;(2)2640
24、(1)200;(2)补图见解析;(3)12;(4)300人.
重庆巴蜀常春藤2023-2024学年数学九上期末综合测试模拟试题含答案: 这是一份重庆巴蜀常春藤2023-2024学年数学九上期末综合测试模拟试题含答案,共9页。试卷主要包含了如图,反比例函数的大致图象为等内容,欢迎下载使用。
2023-2024学年重庆市巴蜀常春藤学校八上数学期末学业水平测试模拟试题含答案: 这是一份2023-2024学年重庆市巴蜀常春藤学校八上数学期末学业水平测试模拟试题含答案,共8页。试卷主要包含了答题时请按要求用笔,下列计算正确的是,若分式的值为零,则的值为等内容,欢迎下载使用。
2023-2024学年重庆巴蜀常春藤数学八上期末经典试题含答案: 这是一份2023-2024学年重庆巴蜀常春藤数学八上期末经典试题含答案,共7页。试卷主要包含了关于的一元二次方程的根的情况,下列命题的逆命题是真命题的是,下列语句中,是命题的为等内容,欢迎下载使用。












