


西藏自治区山南市错那县2022-2023学年数学七年级第二学期期末质量检测模拟试题含答案
展开西藏自治区山南市错那县2022-2023学年数学七年级第二学期期末质量检测模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
请考生注意:
1.请用2B铅笔将选择题答案涂填在答题纸相应位置上,请用0.5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。
2.答题前,认真阅读答题纸上的《注意事项》,按规定答题。
一、选择题(每小题3分,共30分)
1.将一次函数![]() 的图象向上平移2个单位,平移后,若
的图象向上平移2个单位,平移后,若![]() ,则x的取值范围是( )
,则x的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.调查50名学生的年龄,列频数分布表时,这些学生的年龄落在5个小组中,第一、二、三、五组数据个数分别是2,8,15,5,则第四组的频数是( )
A.20 B.30 C.0.4 D.0.6
3.将抛物线![]() 向上平移两个单位长度,再向右平移一个单位长度后,得到的抛物线解析式是( )
向上平移两个单位长度,再向右平移一个单位长度后,得到的抛物线解析式是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.直线y=﹣kx+k﹣3与直线y=kx在同一坐标系中的大致图象可能是( )
A.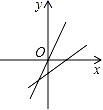 B.
B.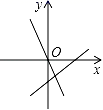 C.
C.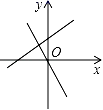 D.
D.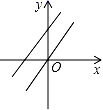
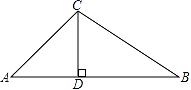
5.如图,在△ABC中,∠A=45°,∠B=30°,CD⊥AB,垂足为D,CD=1,则AB的长为( )
A.![]() B.2
B.2![]() C.
C.![]() D.2
D.2![]()
6.函数y1=x+1与y2=ax+b(a≠0)的图象如图所示,这两个函数图象的交点在y轴上,那么使y1>y2的x的取值范围是( )
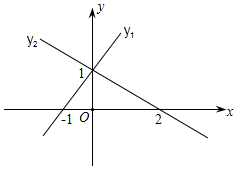
A.x>0 B.x>1 C.x>-1 D.-1<x<2
7.在平面直角坐标系中,点A、B、C、D是坐标轴上的点,![]() ,点
,点![]() ,
,![]() ,点
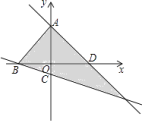
,点![]() 在如图所示的阴影部分内部(不包括边界),则a的取值范围是( )
在如图所示的阴影部分内部(不包括边界),则a的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.若A(a,3),B(1,b)关于x轴对称,则a+b=( )
A.2 B.-2 C.4 D.-4
9.如果分式![]() 有意义,那么x的取值范围是( )
有意义,那么x的取值范围是( )
A.x≠0 B.x≤﹣3 C.x≥﹣3 D.x≠﹣3
10.如图,直线y1=kx+2与直线y2=mx相交于点P(1,m),则不等式mx<kx+2的解集是( )

A.x<0 B.x<1 C.0<x<1 D.x>1
二、填空题(本大题共有6小题,每小题3分,共18分)
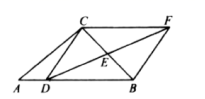
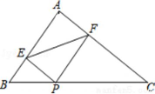
11.如图,在![]() 中,D是AB上任意一点,E是BC的中点,过C作
中,D是AB上任意一点,E是BC的中点,过C作![]() ,交DE的延长线于F,连BF,CD,若
,交DE的延长线于F,连BF,CD,若![]() ,
,![]() ,
,![]() ,则
,则![]() _________.
_________.
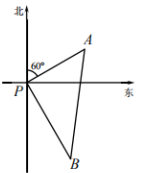
12.如图,某港口P位于南北延伸的海岸线上,东面是大海.“远洋”号、“长峰”号两艘轮船同时离开港口P,各自沿固定方向航行,“远洋”号每小时航行12n mile,“长峰”号每小时航行16n mile,它们离开港东口1小时后,分别到达A,B两个位置,且AB=20n mile,已知“远洋”号沿着北偏东60°方向航行,那么“长峰”号航行的方向是________.
13.在△ABC中,AB=![]() ,AC=5,若BC边上的高等于3,则BC边的长为_____.
,AC=5,若BC边上的高等于3,则BC边的长为_____.
14.如图,Rt△ABC中,∠BAC=90°,AB=6,AC=8,P为BC上一动点,PE⊥AB于E,PF⊥AC于F,则EF最小值是________.
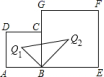
15.如图,边长为![]() 的正方形
的正方形![]() 和边长为
和边长为![]() 的正方形
的正方形![]() 排放在一起,
排放在一起,![]() 和
和![]() 分别是两个正方形的对称中心,则
分别是两个正方形的对称中心,则![]() 的面积为________.
的面积为________.
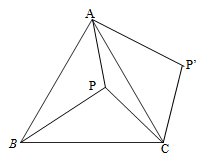
16.如图,![]() 是等边三角形
是等边三角形![]() 内一点,将线段
内一点,将线段![]() 绕点
绕点![]() 顺时针旋转60°得到线段
顺时针旋转60°得到线段![]() ,连接
,连接![]() .若
.若![]() ,
,![]() ,
,![]() ,则四边形
,则四边形![]() 的面积为___________.
的面积为___________.
三、解下列各题(本大题共8小题,共72分)
17.(8分)甲、乙两家采摘园的圣女果品质相同,售价也相同,节日期间,两家均推出优惠方案,甲:游客进园需购买![]() 元门票,采摘的打六折;乙:游客进园不需购买门票,采摘超过一定数量后,超过部分打折,设某游客打算采摘
元门票,采摘的打六折;乙:游客进园不需购买门票,采摘超过一定数量后,超过部分打折,设某游客打算采摘![]()
![]() 千克,在甲、乙采摘园所需总费用为
千克,在甲、乙采摘园所需总费用为![]() 、
、![]() 元,
元,![]() 、
、![]() 与
与![]() 之间的函数关系的图像如图所示.
之间的函数关系的图像如图所示.
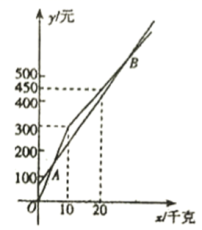
(1)分别求出![]() 、
、![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)求出图中点![]() 、
、![]() 的坐标;
的坐标;
(3)若该游客打算采摘![]() 圣女果,根据函数图像,直接写出该游客选择哪个采摘园更合算.
圣女果,根据函数图像,直接写出该游客选择哪个采摘园更合算.
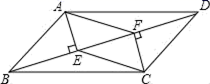
18.(8分)如图,在四边形ABCD中,AB=CD,BF=DE,AE⊥BD,CF⊥BD,垂足分别为E、F.
(1)求证:△ABE≌△CDF;
(2)若AC与BD交于点O,求证:AO=CO.
19.(8分)某风景区计划在绿化区域种植银杏树,现甲、乙两家有相同的银杏树苗可供选择,其具体销售方案如下:
甲 | 乙 | ||
购树苗数量 | 销售单价 | 购树苗数量 | 销售单价 |
不超过500棵时 | 800元/棵 | 不超过1000棵时 | 800元/棵 |
超过500棵的部分 | 700元/棵 | 超过1000棵的部分 | 600元/棵 |
设购买银杏树苗x棵,到两家购买所需费用分别为y甲元、y乙元
(1)该风景区需要购买800棵银杏树苗,若都在甲家购买所要费用为 元,若都在乙家购买所需费用为 元;
(2)当x>1000时,分别求出y甲、y乙与x之间的函数关系式;
(3)如果你是该风景区的负责人,购买树苗时有什么方案,为什么?
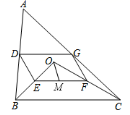
20.(8分)如图,点![]() 是ΔABC内一点,连接OB、OC,并将AB、OB、OC、AC的中点
是ΔABC内一点,连接OB、OC,并将AB、OB、OC、AC的中点![]() 、
、![]() 、
、![]() 、
、![]() 依次连结,得到四边形
依次连结,得到四边形![]() .
.
(1)求证:四边形![]() 是平行四边形;
是平行四边形;
(2)若![]() 为
为![]() 的中点,OM=5,∠OBC与∠OCB互余,求DG的长度.
的中点,OM=5,∠OBC与∠OCB互余,求DG的长度.
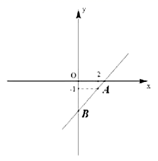
21.(8分)如图为一次函数![]() 的图象,点
的图象,点![]() 分别为该函数图象与
分别为该函数图象与![]() 轴、
轴、![]() 轴的交点.
轴的交点.
(1)求该一次函数的解析式;
(2)求![]() 两点的坐标.
两点的坐标.
22.(10分)计算:(1)![]()
(2)(![]() ﹣1)2﹣(
﹣1)2﹣(![]() ﹣
﹣![]() )(
)(![]() +
+![]() )
)
23.(10分)如图,在△ABC中.AC=BC=5.AB=6.CD是AB边中线.点P从点C出发,以每秒2.5个单位长度的速度沿C-D-C运动.在点P出发的同时,点Q也从点C出发,以每秒2个单位长度的速度沿边CA向点A运动.当一个点停止运动时,另一个点也随之停止,设点P运动的时间为t秒.
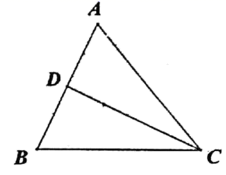
(1)用含t的代数式表示CP、CQ的长度.
(2)用含t的代数式表示△CPQ的面积.
(3)当△CPQ与△CAD相似时,直接写出t的取值范围.
24.(12分)判断代数式![]() 的值能否等于-1?并说明理由.
的值能否等于-1?并说明理由.
参考答案
一、选择题(每小题3分,共30分)
1、B
2、A
3、D
4、B
5、C
6、A
7、D
8、B
9、D
10、B
二、填空题(本大题共有6小题,每小题3分,共18分)
11、1
12、南偏东30°
13、9或1
14、4.8
15、![]()
16、6+4![]()
三、解下列各题(本大题共8小题,共72分)
17、(1)![]() 与
与![]() 之间的函数关系式为
之间的函数关系式为![]() ;
;![]() 与
与![]() 之间的函数关系式为
之间的函数关系式为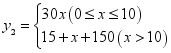 ;(2)
;(2)![]() ;(3)甲
;(3)甲
18、(1)证明见解析;(2)证明见解析.
19、 (1)610000; 1;(2)当x>1000时,y甲=700x+50000,y乙=600x+200000,x为正整数;(3)当0≤x≤500时或x=1500时,到两家购买所需费用一样;当500<x<1500时,到甲家购买合算;当x>1500时,到乙家购买合算.
20、(1)见解析;(2)1.
21、 (1)![]() ;(2)
;(2)![]() ,
,![]() .
.
22、(1)![]() ;(2)
;(2)![]()
23、(1)当0<t≤![]() 时,CP=2.5t,CQ=2t;当
时,CP=2.5t,CQ=2t;当![]() 时,CP=8-2.5t,CQ=2t.
时,CP=8-2.5t,CQ=2t.
(2)当0<t≤![]() 时,S△CPQ=
时,S△CPQ=![]() •PC•sin∠ACD•CQ=
•PC•sin∠ACD•CQ=![]() ×2.5t×
×2.5t×![]() ×2t=
×2t=![]() ;当
;当![]() 时,S△CPQ=
时,S△CPQ=![]() •PC•sin∠ACD•CQ=
•PC•sin∠ACD•CQ=![]() ×(8-2.5t)×
×(8-2.5t)×![]() ×2t=
×2t=![]() .
.
(3)0<t≤![]() 或
或![]() s
s
24、不能,理由见解析
陕西省西安临潼区骊山初级中学2022-2023学年数学七年级第二学期期末质量检测模拟试题含答案: 这是一份陕西省西安临潼区骊山初级中学2022-2023学年数学七年级第二学期期末质量检测模拟试题含答案,共6页。试卷主要包含了方程=1的解的情况为,如图所示,在中,,则为,下列事件中,属于必然事件的是等内容,欢迎下载使用。
广东省中学山纪念中学2022-2023学年七年级数学第二学期期末达标检测模拟试题含答案: 这是一份广东省中学山纪念中学2022-2023学年七年级数学第二学期期末达标检测模拟试题含答案,共8页。试卷主要包含了估计的值应在,函数的图象不经过,一组数等内容,欢迎下载使用。
山东省济南市2022-2023学年七年级数学第二学期期末质量检测模拟试题含答案: 这是一份山东省济南市2022-2023学年七年级数学第二学期期末质量检测模拟试题含答案,共7页。试卷主要包含了正方形有而矩形不一定有的性质是,下列调查中,适合用普查的是,已知是方程的一个根,则等内容,欢迎下载使用。












