


福建省三明建宁县联考2022-2023学年数学七年级第二学期期末教学质量检测试题含答案
展开
这是一份福建省三明建宁县联考2022-2023学年数学七年级第二学期期末教学质量检测试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁,设,,且,则的值是等内容,欢迎下载使用。
福建省三明建宁县联考2022-2023学年数学七年级第二学期期末教学质量检测试题(时间:120分钟 分数:120分) 学校_______ 年级_______ 姓名_______ 考生请注意:1.答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内,不得在试卷上作任何标记。2.第一部分选择题每小题选出答案后,需将答案写在试卷指定的括号内,第二部分非选择题答案写在试卷题目指定的位置上。3.考生必须保证答题卡的整洁。考试结束后,请将本试卷和答题卡一并交回。 一、选择题(每小题3分,共30分)1.为迎接中考体育加试,小刚和小亮分别统计了自己最近10次跳绳比赛,下列统计量中能用来比较两人成绩稳定程度的是 ( )A.平均数 B.中位数 C.众数 D.方差2.若点P的坐标为(3,4 ),则点P关于x轴对称点的点P′的坐标为( )A.(4,-3 ) B.(3,-4 ) C.(-4,3 ) D.(-3,4)3.如图,点O(0,0),A(0,1)是正方形OAA1B的两个顶点,以OA1对角线为边作正方形OA1A2B1,再以正方形的对角线OA2作正方形OA2A3B2,…,依此规律,则点A7的坐标是( )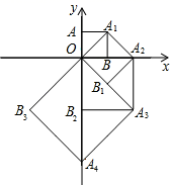 A.(-8,0) B.(8,-8) C.(-8,8) D.(0,16)4.下列二次根式中属于最简二次根式的是( )A.
A.(-8,0) B.(8,-8) C.(-8,8) D.(0,16)4.下列二次根式中属于最简二次根式的是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 5.如图,已知菱形ABCD的周长为24,对角线AC、BD交于点O,且AC+BD=16,则该菱形的面积等于( )
5.如图,已知菱形ABCD的周长为24,对角线AC、BD交于点O,且AC+BD=16,则该菱形的面积等于( )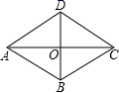 A.6 B.8 C.14 D.286.设
A.6 B.8 C.14 D.286.设![]() ,
,![]() ,且
,且![]() ,则
,则![]() 的值是( )A.
的值是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 7.直角三角形的两边为 9 和 40,则第三边长为( )A.50 B.41 C.31 D.以上答案都不对8.如图,函数
7.直角三角形的两边为 9 和 40,则第三边长为( )A.50 B.41 C.31 D.以上答案都不对8.如图,函数![]() 和
和![]() 的图象相交于A(m,3),则不等式
的图象相交于A(m,3),则不等式![]() 的解集为( )
的解集为( )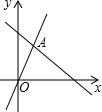 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 9.已知M、N是线段AB上的两点,AM=MN=2,NB=1,以点A为圆心,AN长为半径画弧;再以点B为圆心,BM长为半径画弧,两弧交于点C,连接AC,BC,则△ABC一定是( )A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形10.如图,矩形
9.已知M、N是线段AB上的两点,AM=MN=2,NB=1,以点A为圆心,AN长为半径画弧;再以点B为圆心,BM长为半径画弧,两弧交于点C,连接AC,BC,则△ABC一定是( )A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形10.如图,矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 的中点,
的中点,![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() ,则
,则![]() 的长为( )
的长为( )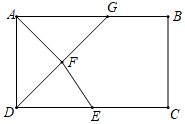 A.3 B.4 C.5 D.6二、填空题(本大题共有6小题,每小题3分,共18分)11.已知一组数据3、a、4、6的平均数为4,则这组数据的中位数是______.12.如图,在边长为1的菱形ABCD中,∠ABC=120°连接对角线AC,以AC为边作第二个菱形ACEF,使∠ACE=120°连接AE,再以AE为边作第三个菱形AEGH,使∠AEG=120°,…,按此规律所作的第n个菱形的边长是________.
A.3 B.4 C.5 D.6二、填空题(本大题共有6小题,每小题3分,共18分)11.已知一组数据3、a、4、6的平均数为4,则这组数据的中位数是______.12.如图,在边长为1的菱形ABCD中,∠ABC=120°连接对角线AC,以AC为边作第二个菱形ACEF,使∠ACE=120°连接AE,再以AE为边作第三个菱形AEGH,使∠AEG=120°,…,按此规律所作的第n个菱形的边长是________.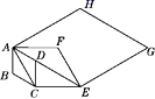 13.如图,在▱ABCD中,
13.如图,在▱ABCD中,![]() ,在边AD上取点E,使
,在边AD上取点E,使![]() ,则
,则![]() 等于______度.
等于______度.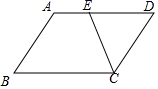 14.如图,是用形状、大小完全相同的等腰梯形镶嵌的图案,则这个图案中的等腰三角形的底角(指锐角)的度数是_____.
14.如图,是用形状、大小完全相同的等腰梯形镶嵌的图案,则这个图案中的等腰三角形的底角(指锐角)的度数是_____.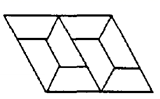 15.如图,四边形
15.如图,四边形![]() 为正方形,点
为正方形,点![]() 分别为
分别为![]() 的中点,其中
的中点,其中![]() ,则四边形
,则四边形![]() 的面积为________________________.
的面积为________________________.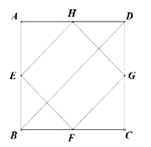 16.甲、乙两人进行射击测试,每人10次射击成绩的平均数都是8.5环,方差分别是:S甲2=2,S乙2=1.5,则射击成绩较稳定的是 (填“甲”或“乙“).三、解下列各题(本大题共8小题,共72分)17.(8分)已知一次函数
16.甲、乙两人进行射击测试,每人10次射击成绩的平均数都是8.5环,方差分别是:S甲2=2,S乙2=1.5,则射击成绩较稳定的是 (填“甲”或“乙“).三、解下列各题(本大题共8小题,共72分)17.(8分)已知一次函数![]() 的图象过点
的图象过点![]() ,
,![]() .(1)求此函数的表达式;(2)若点
.(1)求此函数的表达式;(2)若点![]() 在此函数的图象上,求
在此函数的图象上,求![]() 的值. 18.(8分)如图,在梯形ABCD中,AD∥BC,AB=4,∠C=30°,点E、F分别是边AB、CD的中点,作DP∥AB交EF于点G,∠PDC=90°,求线段GF的长度.
的值. 18.(8分)如图,在梯形ABCD中,AD∥BC,AB=4,∠C=30°,点E、F分别是边AB、CD的中点,作DP∥AB交EF于点G,∠PDC=90°,求线段GF的长度.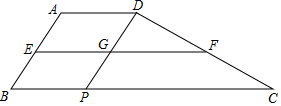 19.(8分)已知下面一列等式:
19.(8分)已知下面一列等式:![]() ;
;![]() ;
;![]() ;
;![]() ;…(1)请你按这些等式左边的结构特征写出它的一般性等式: (2)验证一下你写出的等式是否成立; (3)利用等式计算:
;…(1)请你按这些等式左边的结构特征写出它的一般性等式: (2)验证一下你写出的等式是否成立; (3)利用等式计算:![]()
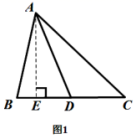
![]() . 20.(8分)请阅读材料,并完成相应的任务.阿波罗尼奥斯(约公元前262~190年),古希腊数学家,与欧几里得、阿基米德齐名.他的著作《圆锥曲线论》是古代世界光辉的科学成果,可以说是代表了希腊几何的最高水平.阿波罗尼奧斯定理,是欧氏几何的定理,表述三角形三边和中线的长度关系,即三角形任意两边的平方和等于第三边的一半与该边中线的平方和的2倍.(1)下面是该结论的部分证明过程,请在框内将其补充完整;已知:如图1所示,在锐角
. 20.(8分)请阅读材料,并完成相应的任务.阿波罗尼奥斯(约公元前262~190年),古希腊数学家,与欧几里得、阿基米德齐名.他的著作《圆锥曲线论》是古代世界光辉的科学成果,可以说是代表了希腊几何的最高水平.阿波罗尼奧斯定理,是欧氏几何的定理,表述三角形三边和中线的长度关系,即三角形任意两边的平方和等于第三边的一半与该边中线的平方和的2倍.(1)下面是该结论的部分证明过程,请在框内将其补充完整;已知:如图1所示,在锐角![]() 中,
中,![]() 为中线..求证:
为中线..求证:![]() 证明:过点
证明:过点![]() 作
作![]() 于点
于点![]()
![]() 为中线
为中线![]() 设
设![]() ,
,![]() ,
,![]()
![]() ,
,![]() 在
在![]() 中,
中,![]() 在
在![]() 中,
中,![]() __________在
__________在![]() 中,
中,![]() __________
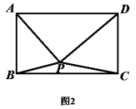
__________![]() __________(2)请直接利用阿波罗尼奧斯定理解决下面问题:如图2,已知点
__________(2)请直接利用阿波罗尼奧斯定理解决下面问题:如图2,已知点![]() 为矩形
为矩形![]() 内任一点,求证:
内任一点,求证:![]() (提示:连接
(提示:连接![]() 、
、![]() 交于点
交于点![]() ,连接
,连接![]() )
) 21.(8分)为加快城市群的建设与发展,在A、B两城市间新建一条城际铁路,建成后,铁路运行里程由现在的210km缩短至180km,平均时速要比现行的平均时速快200km,运行时间仅是现行时间的
21.(8分)为加快城市群的建设与发展,在A、B两城市间新建一条城际铁路,建成后,铁路运行里程由现在的210km缩短至180km,平均时速要比现行的平均时速快200km,运行时间仅是现行时间的![]() ,求建成后的城际铁路在A、B两地的运行时间? 22.(10分)如图,矩形的长
,求建成后的城际铁路在A、B两地的运行时间? 22.(10分)如图,矩形的长![]() ,宽
,宽![]() ,现将矩形的一角沿折痕
,现将矩形的一角沿折痕![]() 翻折,使得
翻折,使得![]() 点落在边
点落在边![]() 上,求点
上,求点![]() 的位置(即的
的位置(即的![]() 长)。
长)。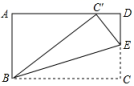 23.(10分)随着生活水平的提高,人们对饮水质量的需求越来越高,我市某公司根据市场需求准备销售A、B两种型号的净水器,每台A型净水器比每台B型净水器进价多300元,用48000元购进A型净水器与用36000元购进B型净水器的数量相等.(1)求每台A型、B型净水器的进价各是多少元?(2)该公司计划购进A、B两种型号的净水器共400台进行销售,其中A型的台数不超过B型的台数,A型净水器每台售价1500元,B型净水器每台售价1100元,怎样安排进货才能使售完这400台净水器所获利润最大?最大利润是多少元? 24.(12分)化简求值:
23.(10分)随着生活水平的提高,人们对饮水质量的需求越来越高,我市某公司根据市场需求准备销售A、B两种型号的净水器,每台A型净水器比每台B型净水器进价多300元,用48000元购进A型净水器与用36000元购进B型净水器的数量相等.(1)求每台A型、B型净水器的进价各是多少元?(2)该公司计划购进A、B两种型号的净水器共400台进行销售,其中A型的台数不超过B型的台数,A型净水器每台售价1500元,B型净水器每台售价1100元,怎样安排进货才能使售完这400台净水器所获利润最大?最大利润是多少元? 24.(12分)化简求值:![]() ,其中m=﹣1. 参考答案 一、选择题(每小题3分,共30分)1、D2、B3、C4、A5、D6、C7、D8、C9、B10、C 二、填空题(本大题共有6小题,每小题3分,共18分)11、3.512、
,其中m=﹣1. 参考答案 一、选择题(每小题3分,共30分)1、D2、B3、C4、A5、D6、C7、D8、C9、B10、C 二、填空题(本大题共有6小题,每小题3分,共18分)11、3.512、![]() 13、114、60°15、4.16、乙 三、解下列各题(本大题共8小题,共72分)17、(1)y=
13、114、60°15、4.16、乙 三、解下列各题(本大题共8小题,共72分)17、(1)y=![]() x+3;(2)a=4;
x+3;(2)a=4;
18、线段GF的长度是419、(1)一般性等式为![]() ;(2)原式成立;详见解析;(3)
;(2)原式成立;详见解析;(3)![]() .20、(1)
.20、(1)![]() ,
,![]() ,
,![]()
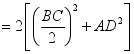 ;(2)见解析21、
;(2)见解析21、![]() h.22、点E在离点D的距离为
h.22、点E在离点D的距离为![]() 处.23、(1)每台A型净水器的进价为2元,每台B型净水器的进价为1元;(2)购进4台A型净水器,4台B型净水器,可使售完这400台净水器所获利润最大,最大利润是100000元.24、m﹣3,-2.
处.23、(1)每台A型净水器的进价为2元,每台B型净水器的进价为1元;(2)购进4台A型净水器,4台B型净水器,可使售完这400台净水器所获利润最大,最大利润是100000元.24、m﹣3,-2.
相关试卷
这是一份福建省三明市建宁县2023-2024学年数学九上期末达标检测模拟试题含答案,共8页。试卷主要包含了若3x=2y,矩形不具备的性质是等内容,欢迎下载使用。
这是一份2023-2024学年福建省三明建宁县联考九年级数学第一学期期末统考试题含答案,共8页。试卷主要包含了下列语句中,正确的有等内容,欢迎下载使用。
这是一份福建省三明建宁县联考2023-2024学年数学八上期末检测试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁,下列运算中,结果正确的是,在四个数中,满足不等式 的有,使分式有意义的的取值范是等内容,欢迎下载使用。









