甘肃省武威市民勤六中学2022-2023学年七年级数学第二学期期末综合测试试题含答案

甘肃省武威市民勤六中学2022-2023学年七年级数学第二学期期末综合测试试题

（时间：120分钟             分数：120分）

学校_______            年级_______        姓名_______

请考生注意：

1．请用2B铅笔将选择题答案涂填在答题纸相应位置上，请用0．5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。

2．答题前，认真阅读答题纸上的《注意事项》，按规定答题。

一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1．如果，那么yx的算术平方根是（　　）

A．2 B．1 C．-1 D．±1

2．正五边形的每个内角度数是（  ）

A．60°                               B．90°                             C．108°    D．120°

3．若点P（2m+1，）在第四象限，则m的取值范围是（    ）

A． B． C． D．

4．正方形具有而菱形不一定具有的性质是（    ）

A．四边相等 B．对角线相等 C．对角线互相垂直 D．对角线互相平分

5．把直线向下平移3个单位长度得到直线为（  ）

A． B． C． D．

6．如图，点是线段的中点，分别以为边作等腰和等腰，，连接，且相交于点，交于点，则下列说法中，不正确的是（   ）

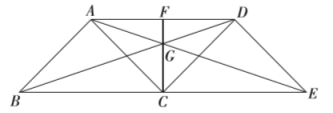
A．是的中线 B．四边形是平行四边形

C． D．平分

7．若式子的值等于0，则x的值为（   ）

A．±2 B．－2 C．2 D．－4

8．如图所示，正方形纸片ABCD中，对角线AC，BD交于点O，折叠正方形纸片ABCD，使AD落在BD上，点A恰好与BD上的点F重合，展开后折痕DE分别交AB，AC于点E，G，连接GF，给出下列结论：

①∠ADG=22.5°；②tan∠AED=2；③S△AGD=S△OGD；④四边形AEFG是菱形；⑤BE=2OG；⑥若S△OGF=1，则正方形ABCD的面积是6+4 ，其中正确的结论个数有（）

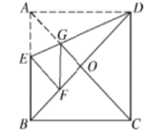
A．2个 B．4个 C．3个 D．5个

9．已知四边形 ABCD ，有以下四个条件：① AB ∥ CD ；② BC ∥ AD ；③ AB  CD ；④ABC  ADC ．从这四个条件中任选两个，能使四边形 ABCD 成为平行四边形的选法有（    ）

A．3 种 B．4 种 C．5 种 D．6 种

10．若x=1是方程x2-2mx+3=0的解，则m的值为（     ）

A． B．2 C． D．-2

11．关于反比例函数y＝的下列说法正确的是（   ）

① 该函数的图象在第二、四象限；

② A（x1、y1）、B（x2、y2）两点在该函数图象上，若x1＜x2，则y1＜y2；

③ 当x＞2时，则y＞－2；

④ 若反比例函数y＝与一次函数y＝x＋b的图象无交点，则b的范围是－4＜b＜4.

A．① ③ B．①④ C．②③ D．②④

12．函数中，自变量x的取值范围是（ ）

A．x＞1 B．x＜1 C． D．

二、填空题（每题4分，满分20分，将答案填在答题纸上）

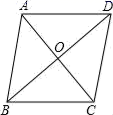
13．如图，菱形ABCD的对角线AC＝3cm，BD＝4cm，则菱形ABCD的面积是_____．

14．若，则y _______（填“是”或“不是”）x的函数.

15．有5张正面分别标有数字-2,0,2,4,6的不透明卡片，它们除数不同外其余全部相同，先将它们背面朝上，洗匀后从中任取一张，将该卡片上的数字记为,则使关于的不等式组有解的概率为____________；

16．在一个不透明的袋子中有若千个小球，这些球除颜色外无其他差别，从袋中随机摸出一球，记下其颜色，这称为一次摸球试验，然后把它重新放回袋中并摇匀，不断重复上述过程．以下是利用计算机模拟的摸球试验统计表：

根据试验所得数据，估计“摸出黑球”的概率是_______（结果保留小数点后一位）．

17．为了改善生态环境，防止水土流失，红旗村计划在荒坡上种树960棵，由于青年志愿者支援，实际每天种树的棵数是原计划的2倍，结果提前4天完成任务，则原计划每天种树的棵数是________.

三、解答题 （本大题共7小题，共64分.解答应写出文字说明、证明过程或演算步骤.）

18．（5分）如图，在中，，点D，E分别是边AB，AC的中点，连接DE，DC，过点A作交DE的延长线于点F，连接CF.

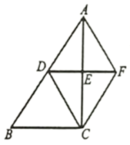
（1）求证：；

（2）求证，四边形BCFD是平行四边形；

（3）若，，求四边形ADCF的面积.

19．（5分）一次函数y =kx+b（）的图象经过点，，求一次函数的表达式．

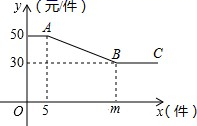
20．（8分）某商店经销某种玩具，该玩具每个进价 20 元，为进行促销，商店制定如下“优惠” 方案：如果一次销售数量不超过 5 个，则每个按 50 元销售：如果一次销售数量超过 5 个，则每增加一个，所有玩具均降低 1 元销售，但单价不得低于 30 元，一次销售该玩具的单价 y（元）与销售数量 x（个）之间的函数关系如下图所示．

（1）结合图形，求出 m 的值；射线 BC 所表示的实际意义是什么；

（2）求线段 AB 满足的 y 与 x 之间的函数解析式，并直接写出自变量的取值范围；

（3）当销售 15 个时，商店的利润是多少元．

21．（10分）平面直角坐标系中，点O为坐标原点，菱形OABC中的顶点B在x轴的正半轴上，点A在反比例函数y=（x＞0）的图象上，点C的坐标为（3，﹣4）．

（1）点A的坐标为_____；

（2）若将菱形OABC沿y轴正方向平移，使其某个顶点落在反比例函数y= （x＞0）的图象上，则该菱形向上平移的距离为_____．

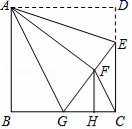
22．（10分）如图，在正方形ABCD中，AB＝6，点E在边CD上，且CE＝2DE，将△ADE沿AE对折得到△AFE，延长EF交边BC于点G，连结AG、CF．

（1）求证：△ABG≌△AFG；

（2）判断BG与CG的数量关系，并证明你的结论；

（3）作FH⊥CG于点H，求GH的长．

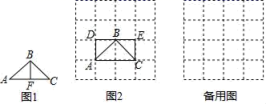
23．（12分）阅读理解

在△ABC中，AB、BC、AC三边的长分别为、、2，求这个三角形的面积．

解法一：如图1，因为△ABC是等腰三角形，并且底AC＝2，根据勾股定理可以求得底边的高AF为1，所以S△ABC＝×2×1＝1．

解法二：建立边长为1的正方形网格，在网格中画出△ABC，使△ABC三个顶点都在小正方形的顶点处，如图2所示，借用网格面积可得S△ABC＝S矩形ADEC﹣S△ABD﹣S△EBC＝1．

方法迁移：请解答下面的问题：

在△ABC中，AB、AC、BC三边的长分别为、、，求这个三角形的面积．

参考答案

一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1、B

2、C

3、C

4、B

5、D

6、D

7、C

8、C

9、B

10、B

11、B

12、C

二、填空题（每题4分，满分20分，将答案填在答题纸上）

13、11cm1

14、不是

15、

16、0.1

17、120

三、解答题 （本大题共7小题，共64分.解答应写出文字说明、证明过程或演算步骤.）

18、（1），见解析；（2）四边形BCFD是平行四边形，见解析；（3）.

19、

20、（1）25、当一次销售数量超过 25 个时，每个均按 30 元销售；（2）线段 AB 满足的 y 与 x 之间的函数解析式是 y=-x+55（5≤x≤25）；（3）此时商店的利润为300元.

21、（1）（3，4）

（2）2或8

22、（1）见解析；（2）BG＝CG；（3）GH＝．

23、S△ABC＝.