湖南省株洲市醴陵市2022-2023学年数学七下期末经典试题含答案

这是一份湖南省株洲市醴陵市2022-2023学年数学七下期末经典试题含答案，共7页。试卷主要包含了五箱梨的质量，对点Q等内容，欢迎下载使用。
湖南省株洲市醴陵市2022-2023学年数学七下期末经典试题（时间：120分钟             分数：120分） 学校_______            年级_______        姓名_______ 请考生注意：1．请用2B铅笔将选择题答案涂填在答题纸相应位置上，请用0．5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。2．答题前，认真阅读答题纸上的《注意事项》，按规定答题。 一、选择题(每小题3分,共30分)1．已知等腰三角形的底角为65°，则其顶角为(  )A．50° B．65° C．115° D．50°或65°2．在中，平分，，则的周长为(    )A． B． C． D．3．如图，一艘巡逻船由A港沿北偏西60°方向航行5海里至B岛，然后再沿北偏东30°方向航行4海里至C岛，则A、C两港相距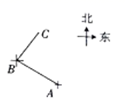（　　）A．4海里 B．海里 C．3海里 D．5海里4．五箱梨的质量（单位：千克）分别为：18，20，21，18，19，则这五箱梨质量的中位数和众数分是（  ）A．20和18 B．20和19 C．18和18 D．19和185．下列关于矩形对角线的说法中，正确的是　　A．对角线相互垂直 B．面积等于对角线乘积的一半C．对角线平分一组对角 D．对角线相等6．如图，等边三角形的边长为4，点是△ABC的中心，，的两边与分别相交于，绕点顺时针旋转时，下列四个结论正确的个数是（   ）①；②；③；④周长最小值是9.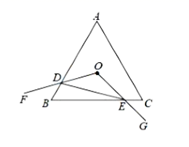A．1个 B．2个 C．3个 D．4个7．对点Q（0，3）的说法正确的是（    ）A．是第一象限的点 B．在轴的正半轴C．在轴的正半轴 D．在轴上8．下列各组条件中，不能判定四边形是平行四边形的是（    ）A．， B．，C．， D．，9．若代数式有意义，则x的取值范围是（　　）A．x≥1 B．x≥0 C．x＞1 D．x＞010．如图，线段AB两端点的坐标分别为A（-1，0），B（1，1），把线段AB平移到CD位置，若线段CD两端点的坐标分别为C（1，a），D（b，4），则a+b的值为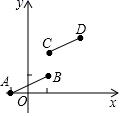（　　）A．7 B．6 C．5 D．4二、填空题(本大题共有6小题，每小题3分，共18分)11．如图，已知AB⊥CD，垂足为点O，直线EF经过O点，若∠1=55°，则∠COE的度数为______度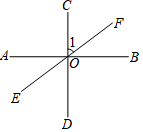．12．在一个不透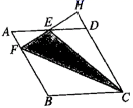明的盒子中装有2个白球和3个红球这些球除了颜色外无其他差别现从这个盒子中任意摸出1个球，那么摸到1个红球的概率是_________.13．某公司需招聘一名员工,对应聘者甲、乙、丙从笔试、面试、体能三个方面进行量化考核.甲、乙、丙各项得分如下表: 笔试面试体能甲837990乙858075丙809073该公司规定：笔试、面试、体能成绩分别不得低于80分，80分，70分，并按60%，30%，10%的比例计入总分，根据总分，从高到低确定三名应聘者的排名顺序，通过计算，乙的总分是82.5，根据规定，将被录用的是__________．14．一组数据共有50个，分成四组后其中前三组的频率分别是0.25、0.15、0.3，则第四组数据的个数为______．15．如图，在菱形中，，过的中点作，垂足为点，与的延长线相交于点，则_______，_______.16．如图,△ABC中，AB=AC=5，BC=6，M为BC的中点,MN⊥AC于N点,则MN=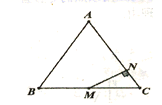（________）．三、解下列各题(本大题共8小题，共72分)17．（8分）如图，在矩形中，点为上一点，连接、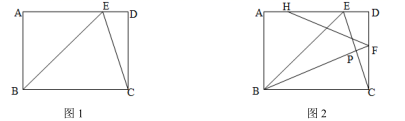，．（1）如图1，若，，求的长．（2）如图2，点是的中点，连接并延长交于，为上一点，连接，且，求证：．   18．（8分）已知：是一元二次方程的两实数根.（1）求 的值；（2）求 x1 x2的值．   19．（8分）在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(−4,5),(−1,3).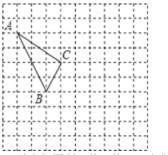(1)请在如图所示的网格平面内作出平面直角坐标系；(2)请作出△ABC关于y轴对称的△DEF，其中点A对应点D，点B对应点E，点C对应点F；(3)写出点E关于原点的对称点M的坐标.   20．（8分）物理兴趣小组位同学在实验操作中的得分情况如下表：得分(分)人数(人)问：（1）这位同学实验操作得分的众数是       ，中位数是       （2）这位同学实验操作得分的平均分是多少？（3）将此次操作得分按人数制成如图所示的扇形统计图．扇形①的圆心角度数是多少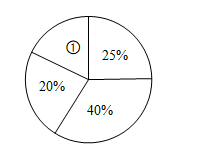？   21．（8分）如图，在平行四边形中，分别为边长的中点，连结．若，则四边形是什么特殊四边形？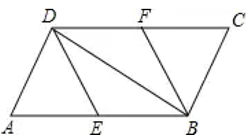请证明你的结论．   22．（10分）如图，在正方形ABCD中，E、F分别为AB、BC的中点，连接CE、DF，将△CBE沿CE对折，得到△CGE，延长EG交CD的延长线于点H。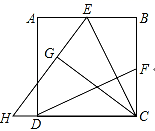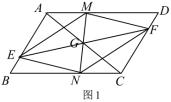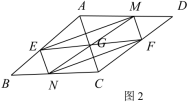（1）求证：CE⊥DF；（2）求的值．   23．（10分）如图，在平面直角坐标系中，的三个顶点分别是、、.(1)画出关于点成中心对称的△；平移，若点的对应点的坐标为，画出平移后对应的△；(2)△和△关于某一点成中心对称，则对称中心的坐标为　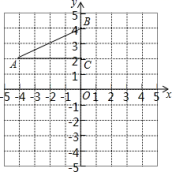 　．   24．（12分）已知：如图1，在中，点为对角线的中点，过点的直线分别交边、于点、，过点的直线分别交边、于点、，且．（1）求证：四边形为平行四边形；（2）如图2，当四边形为矩形时，求证：．       参考答案 一、选择题(每小题3分,共30分)1、A2、C3、B4、D5、D6、B7、B8、B9、A10、B 二、填空题(本大题共有6小题，每小题3分，共18分)11、112、13、乙14、215、1        16、 三、解下列各题(本大题共8小题，共72分)17、（1）；（2）见解析18、（1）27；（2）19、（1）见解析；（2）见解析；（3）(−2,−1).20、（1）9，9；（2）8.75分；（3）54°21、四边形是菱形，证明详见解析22、（1）见解析；（2）.23、 (1)画图见解析；（2）（2，-1）.24、（1）证明见解析；（2）证明见解析．