2022-2023学年湖南省师大附中数学七下期末经典试题含答案

2022-2023学年湖南省师大附中数学七下期末经典试题

（时间：120分钟             分数：120分）

学校_______            年级_______        姓名_______

注意事项

1．考生要认真填写考场号和座位序号。

2．试题所有答案必须填涂或书写在答题卡上，在试卷上作答无效。第一部分必须用2B 铅笔作答；第二部分必须用黑色字迹的签字笔作答。

3．考试结束后，考生须将试卷和答题卡放在桌面上，待监考员收回。

一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1．甲，乙两个样本的容量相同，甲样本的方差为0.102，乙样本的方差是0.06，那么（ ）

A．甲的波动比乙的波动大 B．乙的波动比甲的波动大

C．甲，乙的波动大小一样 D．甲，乙的波动大小无法确定

2．某学校初、高六个年级共有名学生，为了了解其视力情况，现采用抽样调查，如果按的比例抽样，则样本容量是(    )

A． B． C． D．

3．如图，菱形ABCD的对角线AC、BD交于点O，E、F分别是AD、CD边的中点，连接EF，若，，则菱形ABCD的面积是　　

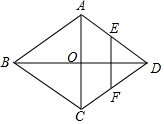
A．24 B．20 C．12 D．6

4．中国传统扇文化有着深厚的底蕴，下列扇面图形是中心对称图形的是(    )

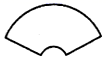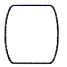A． B． C． D．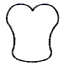

5．若不等式组的解集为﹣1＜x＜1，则（a﹣3）（b+3）的值为（ ）

A．1 B．﹣1 C．2 D．﹣2

6．分式方程的解为（ ）．

A． B． C． D．

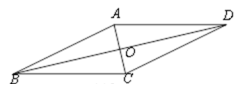
7．如图，ABCD的对角线、交于点，顺次联结ABCD各边中点得到的一个新的四边形，如果添加下列四个条件中的一个条件：①⊥；②；③；④，可以使这个新的四边形成为矩形，那么这样的条件个数是（）

A．1个； B．2个；

C．3个； D．4个．

8．在平面直角坐标系中，点M到x轴的距离是3，到y轴的距离是1，且在第二象限，则点M的坐标是（   ）

A．（3，﹣1） B．（-1，3） C．（-3，1） D．（-2，﹣3）

9．已知△ABC是腰长为1的等腰直角三角形，以Rt△ABC的斜边AC为直角边，画第二个等腰Rt△ACD，再以Rt△ACD的斜边AD为直角边，画第三个等腰Rt△ADE，…，依此类推，第n个等腰直角三角形的面积是(   )

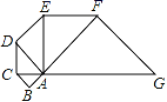
A．2n﹣2 B．2n﹣1 C．2n D．2n+1

10．某校在“我运动，我快乐”的技能比赛培训活动中，在相同条件下，对甲、乙两名同学的“单手运球”项目进行了5次测试，测试成绩（单位：分）如下：根据右图判断正确的是（  ）

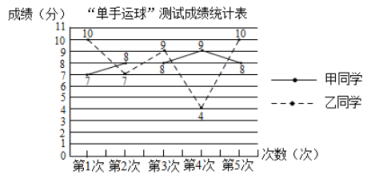
A．甲成绩的平均分低于乙成绩的平均分；

B．甲成绩的中位数高于乙成绩的中位数；

C．甲成绩的众数高于乙成绩的众数；

D．甲成绩的方差低于乙成绩的方差．

11．甲、乙、丙、丁四人参加训练，近期的10次百米测试平均成绩都是13.2s，方差如下表：

则这四人中发挥最稳定的是(　　)

A．甲 B．乙 C．丙 D．丁

12．等于(    )

A．2 B．0 C． D．-2019

二、填空题（每题4分，满分20分，将答案填在答题纸上）

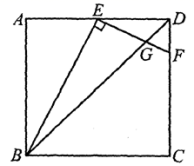
13．如图，在边长为2的正方形ABCD中，点E是边AD中点，点F在边CD上，且FE⊥BE，设BD与EF交于点G，则△DEG的面积是___

14．若x=-1， 则x2+2x+1=__________.

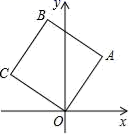
15．如图，将正方形OABC放在平面直角坐标系中，O是坐标原点，点A的坐标是（2，3），则C点坐标是_____．

16．抛物线，当随的增大而减小时的取值范围为______.

17．已知y=++9，则（xy-64）2的平方根为______．

三、解答题 （本大题共7小题，共64分.解答应写出文字说明、证明过程或演算步骤.）

18．（5分）在平面直角坐标系中，过一点分别作x轴，y轴的垂线，如果由这点、原点及两个垂足为顶点的矩形的周长与面积相等，那么称这个点是平面直角坐标系中的“巧点”．例如，图1中过点P（4，4）分別作x轴，y轴的垂线，垂足为A，B，矩形OAPB的周长为16，面积也为16，周长与面积相等，所以点P是巧点．请根据以上材料回答下列问题：

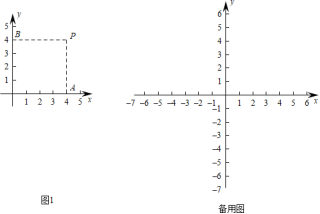
（1）已知点C（1，3），D（-4，-4），E（5，-），其中是平面直角坐标系中的巧点的是______；

（2）已知巧点M（m，10）（m＞0）在双曲线y=（k为常数）上，求m，k的值；

（3）已知点N为巧点，且在直线y=x+3上，求所有满足条件的N点坐标．

19．（5分）如图，在中，AD平分交BC于点D，F为AD上一点，且，BF的延长线交AC于点E．

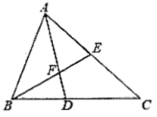
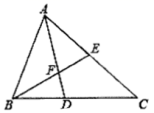
   备用图

（1）求证：；

（2）若，，，求DF的长；

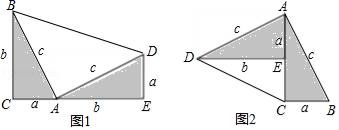
20．（8分）勾股定理神秘而美妙，它的证法多样，其巧妙各有不同，其中的“面积法”给了小聪以灵感，他惊喜的发现，当两个全等的直角三角形如图1或图1摆放时，都可以用“面积法”来证明，请你利用图1或图1证明勾股定理（其中∠DAB＝90°）

求证：a1+b1＝c1．

21．（10分）解方程

（1）

（2）

（3）

22．（10分）某公司经营甲、乙两种商品，两种商品的进价和售价情况如下表：

两种商品的进价和售价始终保持不变．现准备购进甲、乙两种商品共20件．设购进甲种商品件，两种商品全部售出可获得利润为万元．

（1）与的函数关系式为__________________；

（2）若购进两种商品所用的资金不多于200万元，则该公司最多购进多少合甲种商品？

（3）在（2）的条件下，请你帮该公司设计一种进货方案，使得该公司获得最大利润，并求出最大利润是多少？

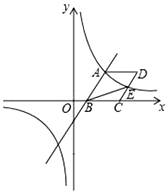
23．（12分）如图，已知一次函数的图象与反比例函数第一象限内的图象相交于点，与轴相交于点.

(1)求和的值；

(2)观察反比例函数的图象，当时，请直接写出的取值范围；

(3)如图，以为边作菱形，使点在轴正半轴上，点在第一象限，双曲线交于点，连接、，求.

参考答案

一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1、A

2、C

3、A

4、C

5、D

6、C

7、C

8、B

9、A

10、D

11、B

12、C

二、填空题（每题4分，满分20分，将答案填在答题纸上）

13、

14、2

15、（﹣3，2）．

16、（也可以）

17、±1

三、解答题 （本大题共7小题，共64分.解答应写出文字说明、证明过程或演算步骤.）

18、（1）D和E；（2）m=，k=25；（3）N的坐标为(-6，-3)或(3，6)．

19、（1）详见解析；（2）

20、见解析.

21、（1） （2） （3）

22、（1）w＝0.5x+40；（2）10；（3）该公司购进甲种商品10件，乙种商品10件时，该公司获得最大利润，最大利润是45万元

23、 (1)n=3，k=12；(2)或；(3)S△ABE=.