


浙江省温州市各学校2022-2023学年数学七年级第二学期期末质量检测模拟试题含答案
展开
这是一份浙江省温州市各学校2022-2023学年数学七年级第二学期期末质量检测模拟试题含答案,共7页。试卷主要包含了7 的小数部分是等内容,欢迎下载使用。
浙江省温州市各学校2022-2023学年数学七年级第二学期期末质量检测模拟试题(时间:120分钟 分数:120分) 学校_______ 年级_______ 姓名_______ 考生须知:1.全卷分选择题和非选择题两部分,全部在答题纸上作答。选择题必须用2B铅笔填涂;非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。2.请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。3.保持卡面清洁,不要折叠,不要弄破、弄皱,在草稿纸、试题卷上答题无效。 一、选择题(每小题3分,共30分)1.如图,已知在平行四边形![]() 中,
中,![]() 是对角线
是对角线![]() 上的两点,则以下条件不能判断四边形
上的两点,则以下条件不能判断四边形![]() 是平行四边形的是( )
是平行四边形的是( )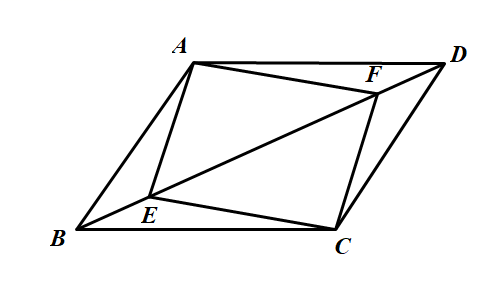 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 2.使分式
2.使分式![]() 有意义的x的取值范围是( )A.x≥1 B.x≤1 C.x≠1 D.x>13.如果一个正多边形的中心角为60°,那么这个正多边形的边数是( )A.4 B.5 C.6 D.74.如图所示图形中既是中心对称图形,又能镶嵌整个平面的有( )
有意义的x的取值范围是( )A.x≥1 B.x≤1 C.x≠1 D.x>13.如果一个正多边形的中心角为60°,那么这个正多边形的边数是( )A.4 B.5 C.6 D.74.如图所示图形中既是中心对称图形,又能镶嵌整个平面的有( )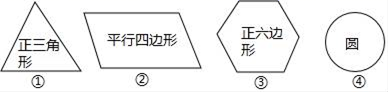 A.①②③④ B.①②③ C.②③ D.③5.如图,△ABC中,∠C=90°,AC=3,∠B=30°,点P是BC边上的动点,则AP的长不可能是( )
A.①②③④ B.①②③ C.②③ D.③5.如图,△ABC中,∠C=90°,AC=3,∠B=30°,点P是BC边上的动点,则AP的长不可能是( )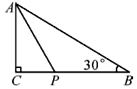 A.3.5 B.4.2 C.5.8 D.76.如图,已知菱形ABCD的边长为2,∠DAB=60°,则对角线BD的长是( )
A.3.5 B.4.2 C.5.8 D.76.如图,已知菱形ABCD的边长为2,∠DAB=60°,则对角线BD的长是( )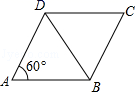 A.1 B.
A.1 B.![]() C.2 D.
C.2 D.![]() 7.如图,平行四边形ABCD的对角线AC与BD相交于点O,AE⊥BC于E,AB=
7.如图,平行四边形ABCD的对角线AC与BD相交于点O,AE⊥BC于E,AB=![]() ,AC=2,BD=4,则AE的长为( )
,AC=2,BD=4,则AE的长为( )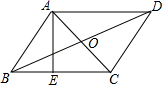 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 8.甲、乙是两个不透明的纸箱,甲中有三张标有数字
8.甲、乙是两个不透明的纸箱,甲中有三张标有数字![]() ,
,![]() ,
,![]() 的卡片,乙中有三张标有数字
的卡片,乙中有三张标有数字![]() ,
,![]() ,
,![]() 的卡片,卡片除所标数字外无其他差别,现制定一个游戏规则:从甲中任取一张卡片,将其数字记为
的卡片,卡片除所标数字外无其他差别,现制定一个游戏规则:从甲中任取一张卡片,将其数字记为![]() ,从乙中任取一张卡片,将其数字记为
,从乙中任取一张卡片,将其数字记为![]() .若
.若![]() ,
,![]() 能使关于
能使关于![]() 的一元二次方程
的一元二次方程![]() 有两个不相等的实数根,则甲获胜;否则乙获胜.则乙获胜的概率为( )A.
有两个不相等的实数根,则甲获胜;否则乙获胜.则乙获胜的概率为( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 9.如图,将
9.如图,将![]() 绕点
绕点![]() 按顺时针旋转一定角度得到
按顺时针旋转一定角度得到![]() ,点
,点![]() 的对应点
的对应点![]() 恰好落在
恰好落在![]() 边上.若
边上.若![]() ,
,![]() ,则
,则![]() 的长为( )
的长为( )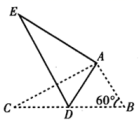 A.1 B.
A.1 B.![]() C.2 D.
C.2 D.![]() 10.7
10.7 ![]() 的小数部分是( )A.4 -
的小数部分是( )A.4 -![]() B.3
B.3 ![]() C.4
C.4 ![]() D.3
D.3 ![]() 二、填空题(本大题共有6小题,每小题3分,共18分)11.函数
二、填空题(本大题共有6小题,每小题3分,共18分)11.函数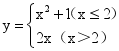 ,则当函数值y=8时,自变量x的值是_____.12.如图,在菱形ABCD中,E,F分别是AD,BD的中点,若EF=2,则菱形ABCD的周长是__.
,则当函数值y=8时,自变量x的值是_____.12.如图,在菱形ABCD中,E,F分别是AD,BD的中点,若EF=2,则菱形ABCD的周长是__.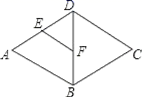 13.如图,在平面直角坐标系中,矩形OABC的顶点A、C的坐标分别为
13.如图,在平面直角坐标系中,矩形OABC的顶点A、C的坐标分别为![]() ,
,![]() ,
,![]() ,点P在BC(不与点B、C重合)上运动,当△ODP是腰长为5的等腰三角形时,点P的坐标为______.
,点P在BC(不与点B、C重合)上运动,当△ODP是腰长为5的等腰三角形时,点P的坐标为______. 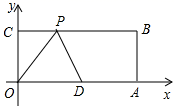 14.一个n边形的内角和为1080°,则n=________.15.如果关于x的方程
14.一个n边形的内角和为1080°,则n=________.15.如果关于x的方程![]() +1有增根,那么k的值为_____16.如图,已知
+1有增根,那么k的值为_____16.如图,已知![]() , AD平分
, AD平分![]() 于点E,
于点E,![]() ,则BC= ___cm。
,则BC= ___cm。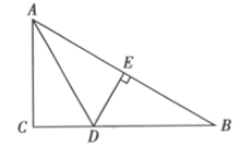 三、解下列各题(本大题共8小题,共72分)17.(8分)如图,
三、解下列各题(本大题共8小题,共72分)17.(8分)如图,![]() 、
、![]() 是
是![]() 的对角线
的对角线![]() 上的两点,且
上的两点,且![]() ,
,![]() ,连接
,连接![]() 、
、![]() 、
、![]() 、
、![]() .
. (1)求证:四边形
(1)求证:四边形![]() 为平行四边形;(2)若
为平行四边形;(2)若![]() ,
,![]() ,求
,求![]() 的长. 18.(8分)已知正方形
的长. 18.(8分)已知正方形![]() ,直线
,直线![]() 垂直平分线段
垂直平分线段![]() ,点
,点![]() 是直线
是直线![]() 上一动点,连结
上一动点,连结![]() ,将线段
,将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到线段
得到线段![]() ,连接
,连接![]() .(1)如图
.(1)如图![]() ,点
,点![]() 在正方形内部,连接
在正方形内部,连接![]() ,求
,求![]() 的度数;(2)如图
的度数;(2)如图![]() ,点
,点![]() 在正方形内部,连接
在正方形内部,连接![]() ,若
,若![]() ,求
,求![]() 的值.
的值.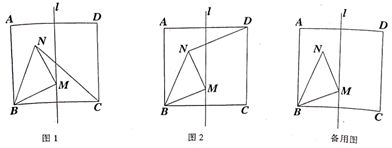 19.(8分)在直角坐标系中,已知两点的坐标是M(x1,y1),N(x2,y2),M,N两点之间的距离,可以用公式MN=
19.(8分)在直角坐标系中,已知两点的坐标是M(x1,y1),N(x2,y2),M,N两点之间的距离,可以用公式MN=![]() 计算.解答下列问题:(1)若已知点A(1,2),B(4,-2),求A,B两点间的距离;(2)在(1)的条件下,点O是坐标原点,判断△AOB是什么三角形,并说明理由. 20.(8分)(1)下列关于反比例函数y=
计算.解答下列问题:(1)若已知点A(1,2),B(4,-2),求A,B两点间的距离;(2)在(1)的条件下,点O是坐标原点,判断△AOB是什么三角形,并说明理由. 20.(8分)(1)下列关于反比例函数y=![]() 的性质,描述正确的有_____。(填所有描述正确的选项)A. y随x的增大而减小B. 图像关于原点中心对称C. 图像关于直线y=x成轴对称D. 把双曲线y=
的性质,描述正确的有_____。(填所有描述正确的选项)A. y随x的增大而减小B. 图像关于原点中心对称C. 图像关于直线y=x成轴对称D. 把双曲线y=![]() 绕原点逆时针旋转90°可以得到双曲线y=-
绕原点逆时针旋转90°可以得到双曲线y=-![]() (2)如图,直线AB、CD经过原点且与双曲线y=
(2)如图,直线AB、CD经过原点且与双曲线y=![]() 分别交于点A、B、C、D,点A、C的横坐标分别为m,n(m>n>0),连接AC、CB、BD、DA。①判断四边形ACBD的形状,并说明理由;②当m、n满足怎样的数量关系时,四边形ACBD是矩形?请直接写出结论;③若点A的横坐标m=3,四边形ACBD的面积为S,求S与n之间的函数表达式。
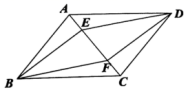
分别交于点A、B、C、D,点A、C的横坐标分别为m,n(m>n>0),连接AC、CB、BD、DA。①判断四边形ACBD的形状,并说明理由;②当m、n满足怎样的数量关系时,四边形ACBD是矩形?请直接写出结论;③若点A的横坐标m=3,四边形ACBD的面积为S,求S与n之间的函数表达式。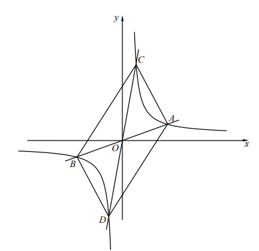 21.(8分)已知:AC是菱形ABCD的对角线,且AC=BC.
21.(8分)已知:AC是菱形ABCD的对角线,且AC=BC.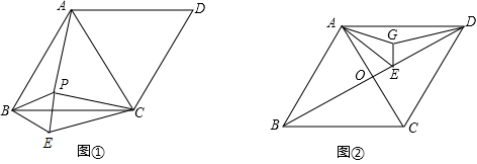 (1)如图①,点P是△ABC的一个动点,将△ABP绕着点B旋转得到△CBE.①求证:△PBE是等边三角形;②若BC=5,CE=4,PC=3,求∠PCE的度数;(2)连结BD交AC于点O,点E在OD上且DE=3,AD=4,点G是△ADE内的一个动点如图②,连结AG,EG,DG,求AG+EG+DG的最小值. 22.(10分)已知一次函数
(1)如图①,点P是△ABC的一个动点,将△ABP绕着点B旋转得到△CBE.①求证:△PBE是等边三角形;②若BC=5,CE=4,PC=3,求∠PCE的度数;(2)连结BD交AC于点O,点E在OD上且DE=3,AD=4,点G是△ADE内的一个动点如图②,连结AG,EG,DG,求AG+EG+DG的最小值. 22.(10分)已知一次函数![]() 与正比例函数
与正比例函数![]() 都经过点
都经过点![]() ,
,![]() 的图像与
的图像与![]() 轴交于点
轴交于点![]() ,且
,且![]() .(1)求
.(1)求![]() 与
与![]() 的解析式;(2)求⊿
的解析式;(2)求⊿![]() 的面积. 23.(10分)已知函数
的面积. 23.(10分)已知函数![]() ,试回答:(1)
,试回答:(1)![]() 为何值时,
为何值时,![]() 随
随![]() 的增大而增大;(2)
的增大而增大;(2)![]() 为何值时,图象过点
为何值时,图象过点![]() . 24.(12分)如图,在
. 24.(12分)如图,在![]() 中,点
中,点![]() 为边
为边![]() 的中点,点
的中点,点![]() 在
在![]() 内,
内,![]() 平分
平分![]() 点
点![]() 在
在![]() 上,
上,![]() .
.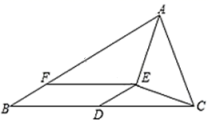 (1)求证:四边形
(1)求证:四边形![]() 是平行四边形;(2)线段
是平行四边形;(2)线段![]() 之间具有怎样的数量关系?证明你所得到的结论. 参考答案 一、选择题(每小题3分,共30分)1、A2、C3、C4、C5、D6、C7、D8、C9、C10、A 二、填空题(本大题共有6小题,每小题3分,共18分)11、
之间具有怎样的数量关系?证明你所得到的结论. 参考答案 一、选择题(每小题3分,共30分)1、A2、C3、C4、C5、D6、C7、D8、C9、C10、A 二、填空题(本大题共有6小题,每小题3分,共18分)11、![]() 或412、113、(1,3)或(4,3)14、115、416、1 三、解下列各题(本大题共8小题,共72分)17、(1)证明见解析 (2)
或412、113、(1,3)或(4,3)14、115、416、1 三、解下列各题(本大题共8小题,共72分)17、(1)证明见解析 (2)![]() 18、(1)
18、(1)![]() ;(2)
;(2)![]() .19、(1)A,B两点间的距离AB=5;(2)△AOB是直角三角形,见解析.20、(1)ABCD;(2)①见解析;②
.19、(1)A,B两点间的距离AB=5;(2)△AOB是直角三角形,见解析.20、(1)ABCD;(2)①见解析;②![]() ∴当
∴当![]() 时,四边形ACBD是矩形;③S=
时,四边形ACBD是矩形;③S=![]() 21、(1)①见解析,②∠PCE=30°;(2)AG+EG+DG的最小值为1.22、(1)
21、(1)①见解析,②∠PCE=30°;(2)AG+EG+DG的最小值为1.22、(1)![]() 或
或![]() ;⊿
;⊿![]() 的面积为15个平方单位. 23、(1)
的面积为15个平方单位. 23、(1)![]() ;(2)
;(2)![]() 24、(1)见详解;(2)
24、(1)见详解;(2)![]() ,证明见详解.
,证明见详解.
相关试卷
这是一份2023-2024学年浙江省温州市永嘉县数学八上期末质量检测模拟试题含答案,共8页。试卷主要包含了如图,时钟在下午4等内容,欢迎下载使用。
这是一份2023-2024学年浙江省温州市实验学校八年级数学第一学期期末教学质量检测模拟试题含答案,共7页。试卷主要包含了关于一次函数,下列结论正确的是,平面直角坐标系中,点P等内容,欢迎下载使用。
这是一份浙江省温州市龙湾区2022-2023学年七年级数学第二学期期末检测模拟试题含答案,共7页。








