浙江省江北区2022-2023学年七年级数学第二学期期末教学质量检测试题含答案

浙江省江北区2022-2023学年七年级数学第二学期期末教学质量检测试题

（时间：120分钟             分数：120分）

学校_______            年级_______        姓名_______

考生须知：

1．全卷分选择题和非选择题两部分，全部在答题纸上作答。选择题必须用2B铅笔填涂；非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。

2．请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。

3．保持卡面清洁，不要折叠，不要弄破、弄皱，在草稿纸、试题卷上答题无效。

一、选择题(每小题3分,共30分)

1．已知一组数据1，2，3，，它们的平均数是2，则这一组数据的方差为（    ）

A．1 B．2 C．3 D．

2．下列数据中不能作为直角三角形的三边长是（　　）

A．1、1、 B．5、12、13 C．3、5、7 D．6、8、10

3．甲，乙两班举行电脑汉字输入速度比赛，参赛学生每分钟输入汉字的个数经统计计算后，结果如下。 某同学根据上表分析，得出如下结论。

（1）甲，乙两班学生成绩的平均水平相同。

（2）乙班优秀的人数多于甲班优秀的人数。（每分钟输入汉字≧150个为优秀。）

（3）甲班成绩的波动情况比乙班成绩的波动小。

上述结论中正确的是（        ）

A．(1) (2)  (3) B．(1) (2) C．(1) (3) D．(2)(3)

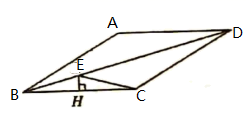
4．如图，菱形中，点为对角线上一点，且于点，连接，若，则的度数为（  ）

A． B． C． D．

5．已知a是方程2x2﹣4x﹣2019＝0的一个解，则a2﹣2a＝（　　）

A．2019 B．4038 C． D．

6．在中，平分，，则的周长为(    )

A． B． C． D．

7．如图，剪两张对边平行且宽度相同的纸条随意交叉叠放在一起，转动其中一张，重合部分构成一个四边形，则下列结论中不一定成立的是（　　）

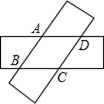
A．∠ABC＝∠ADC，∠BAD＝∠BCD B．AB＝BC

C．AB＝CD，AD＝BC D．∠DAB+∠BCD＝180°

8．已知一次函数上有两点，，若，则、的关系是（   ）

A． B． C． D．无法判断

9．如图，□ABCD中，EF过对角线的交点O，AB=4，AD=3，OF=1.3，则四边形BCEF的周长为（    ）

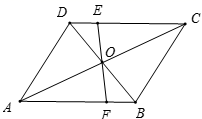
A．8.3 B．9.6 C．12.6 D．13.6

10．有5张边长为2的正方形纸片，4张边长分别为2、3的矩形纸片，6张边长为3的正方形纸片，从其中取出若干张纸片，且每种纸片至少取一张，把取出的这些纸片拼成一个正方形（原纸张进行无空隙、无重叠拼接），则拼成正方形的边长最大为（）

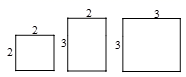
A．6 B．7 C．8 D．9

二、填空题(本大题共有6小题，每小题3分，共18分)

11．花粉的质量很小．一粒某种植物花粉的质量约为0.000 037毫克，那么0.000 037毫克可用科学记数法表示为________毫克.

12．工人师傅给一幅长为，宽为的矩形书法作品装裱，作品的四周需要留白如图所示，已知左、右留白部分的宽度一样，上、下留白部分的宽度也一样，而且左侧留白部分的宽度是上面留白部分的宽度的2倍，使得装裱后整个挂图的面积为. 设上面留白部分的宽度为，可列得方程为________。

13．已知一次函数的图象过点（3，5）与点（-4，-9），则这个一次函数的解析式为____________.

14．若一次函数中，随的增大而减小，则的取值范围是______．

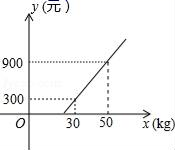
15．某航空公司规定，乘客所携带行李的重量x（kg）与运费y（元）满足如图所示的函数图象，那么每位乘客最多可免费携带____kg的行李．

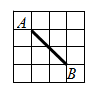
16．如图，在边长为1的小正方形组成的网格中，点A，B都在格点上，则线段AB的长度为_________．

三、解下列各题(本大题共8小题，共72分)

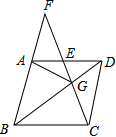
17．（8分）如图，在菱形ABCD中，G是BD上一点，连接CG并延长交BA的延长线于点F，交AD于点E．

（1）求证：AG=CG；

（2）求证：AG2=GE·GF．

18．（8分）在正方形中，连接，为射线上的一个动点（与点不重合），连接，的垂直平分线交线段于点，连接，.

提出问题：当点运动时，的度数是否发生改变？

探究问题：

（1）首先考察点的两个特殊位置：

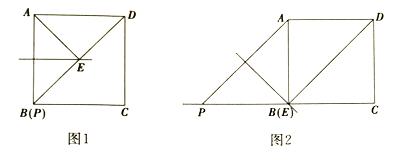
①当点与点重合时，如图1所示，____________

②当时，如图2所示，①中的结论是否发生变化？直接写出你的结论：__________；（填“变化”或“不变化”）

（2）然后考察点的一般位置：依题意补全图3，图4，通过观察、测量，发现：（1）中①的结论在一般情况下_________；（填“成立”或“不成立”）

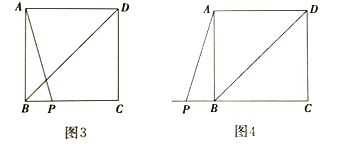
（3）证明猜想：若（1）中①的结论在一般情况下成立，请从图3和图4中任选一个进行证明；若不成立，请说明理由.

19．（8分）如图，在□ABCD中，AB=10，AD=8，AC⊥BC，求□ABCD的面积．

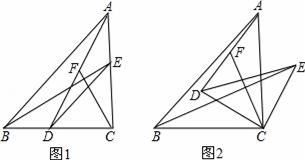
20．（8分）已知△ABC和△DEC都是等腰直角三角形，C为它们的公共直角顶点，D、E分别在BC、AC边上．

(1)如图1，F是线段AD上的一点，连接CF，若AF=CF；

①求证：点F是AD的中点；

②判断BE与CF的数量关系和位置关系，并说明理由；

(2)如图2，把△DEC绕点C顺时针旋转α角（0＜α＜90°），点F是AD的中点，其他条件不变，判断BE与CF的关系是否不变？若不变，请说明理由；若要变，请求出相应的正确结论．

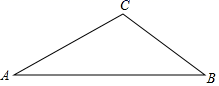
21．（8分）如图，在△ABC中，，，，求AB的长．

22．（10分）解方程：x2﹣2x＝1．

23．（10分）计算

（1）   

（2）

（3）                    

（4）（+3﹣2）×2

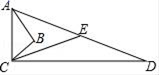
24．（12分）如图，∠B＝90°，AB＝4，BC＝3，CD＝l2，AD＝13，点E是AD的中点，求CE的长．

参考答案

一、选择题(每小题3分,共30分)

1、D

2、C

3、B

4、A

5、C

6、C

7、D

8、A

9、B

10、C

二、填空题(本大题共有6小题，每小题3分，共18分)

11、

12、（120+4x）（40+2x）＝1

13、

14、

15、2

16、

三、解下列各题(本大题共8小题，共72分)

17、（1）证明见解析；（2）证明见解析.

18、（1）①45；②不变化；（2）成立；（3）详见解析.

19、48

20、（1）①证明见解析；②BE=2CF，BE⊥CF；（2）仍然有BE=2CF，BE⊥CF．

21、AB=9+4.

22、，．

23、（1）（2）（3） （4）1+1

24、6.1