


浙江省宁波市国际学校2022-2023学年数学七年级第二学期期末学业质量监测模拟试题含答案
展开浙江省宁波市国际学校2022-2023学年数学七年级第二学期期末学业质量监测模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项
1.考生要认真填写考场号和座位序号。
2.试题所有答案必须填涂或书写在答题卡上,在试卷上作答无效。第一部分必须用2B 铅笔作答;第二部分必须用黑色字迹的签字笔作答。
3.考试结束后,考生须将试卷和答题卡放在桌面上,待监考员收回。
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.若分式![]() 无意义,则x等于( )
无意义,则x等于( )
A.﹣![]() B.0 C.
B.0 C.![]() D.
D.![]()
2.直线![]() 与直线
与直线![]() 的交点不可能在( )
的交点不可能在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.一个直角三角形两条直角边的长分别为5,12,则其斜边上的高为( )
A.![]() B.13 C.6 D.25
B.13 C.6 D.25
4.一次函数![]() 与
与![]() ,在同一平面直角坐标系中的图象是( )
,在同一平面直角坐标系中的图象是( )
A.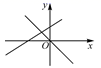 B.
B.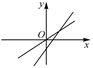 C.
C.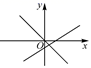 D.
D.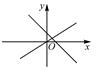
5.在![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,中分式的个数有( )
,中分式的个数有( )
A.2个 B.3个 C.4个 D.5个
6.观察下列命题:
(1)如果a<0,b>0,那么a+b<0;
(2)如果两个三角形的3个角对应相等,那么这两个三角形全等;
(3)同角的补角相等;
(4)直角都相等.
其中真命题的个数是( ).
A.0 B.1 C.2 D.3
7.下列各组线段中,能够组成直角三角形的一组是( )
A.1,2,3 B.2,3,4 C.4,5,6 D.1,![]() ,2
,2
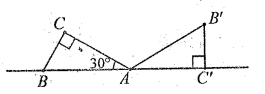
8.如图,将一个含![]() 角的直角三角板
角的直角三角板![]() 绕点
绕点![]() 旋转,得点
旋转,得点![]() ,
,![]() ,
,![]() ,在同一条直线上,则旋转角
,在同一条直线上,则旋转角![]() 的度数是( )
的度数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
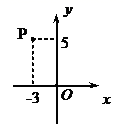
9.如图,在平面直角坐标系xOy中,点P(![]() ,5)关于y轴的对称点的坐标为( )
,5)关于y轴的对称点的坐标为( )
A.(![]() ,
,![]() ) B.(1,5) C.(1.
) B.(1,5) C.(1.![]() ) D.(5,
) D.(5,![]() )
)
10.一个等腰三角形的周长为14,其一边长为4那么它的底边长为( )
A.5 B.4 C.6 D.4或6
11.一次函数y=kx+b(k,b是常数,k≠0)的图象如图所示,则不等式kx+b>0的解集为( )
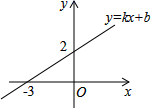
A.x>-3 B.x>0 C.x<-2 D.x<0
12.下列式子属于最简二次根式的是( )
A.![]() B.
B.![]() C.
C.![]() (a>0) D.
(a>0) D.![]()
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13.比较大小:![]() (填“>”或“<”或“=”).
(填“>”或“<”或“=”).
14.已知关于![]() 的分式方程
的分式方程![]() 的解为负数,则
的解为负数,则![]() 的取值范围是 .
的取值范围是 .
15.若一个直角三角形的其中两条边长分别为6和8,则第三边长为_____.
16.因式分解:x2﹣9y2= .
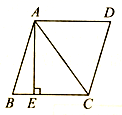
17.如图,在菱形ABCD中,AB=5,对角线AC=1.若过点A作AE⊥BC,垂足为E,则AE的长为_________.
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
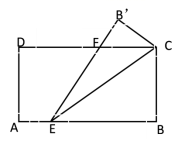
18.(5分)如图,将矩形纸沿着CE所在直线折叠,B点落在B’处,CD与EB’交于点F,如果AB=10cm,AD=6cm,AE=2cm,求EF的长。
19.(5分)实践与探究
宽与长的比是![]() (约0.618)的矩形叫做黄金矩形。黄金矩形给我们以协调、均匀的美感。世界各国许多著名的建筑,为取得最佳的视觉效果,都采用了黄金矩形的设计。
(约0.618)的矩形叫做黄金矩形。黄金矩形给我们以协调、均匀的美感。世界各国许多著名的建筑,为取得最佳的视觉效果,都采用了黄金矩形的设计。
下面我们通过折纸得到黄金矩形。
第一步,在一张矩形纸片的一端,利用图1的方法折出一个正方形,然后把纸片展平。
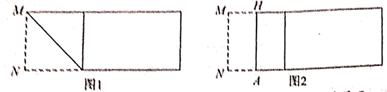
第二步,如图2,把这个正方形折成两个相等的矩形,再把纸片展平,折痕是![]() 。
。
第三步,折出内侧矩形的对角线![]() ,并把
,并把![]() 折到图3中所示的
折到图3中所示的![]() 处,折痕为
处,折痕为![]() 。
。
第四步,展平纸片,按照所得的点![]() 折出
折出![]() ,使
,使![]() ;过点
;过点![]() 折出折痕
折出折痕![]() ,使
,使![]() 。
。
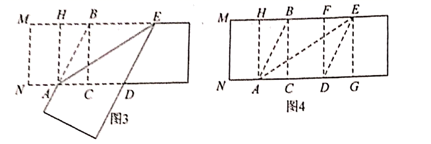
(1)上述第三步将![]() 折到
折到![]() 处后,得到一个四边形
处后,得到一个四边形![]() ,请判断四边形
,请判断四边形![]() 的形状,并说明理由。
的形状,并说明理由。
(2)上述第四步折出折痕![]() 后得到一个四边形
后得到一个四边形![]() ,这个四边形是黄金矩形,请你说明理由。(提示:设
,这个四边形是黄金矩形,请你说明理由。(提示:设![]() 的长度为2)
的长度为2)
(3)在图4中,再找出一个黄金矩形_______________________________(黄金矩形![]() 除外,直接写出答案,不需证明,可能参考数值:
除外,直接写出答案,不需证明,可能参考数值:![]() )
)
(4)请你举一个采用了黄金矩形设计的世界名建筑_________________________.
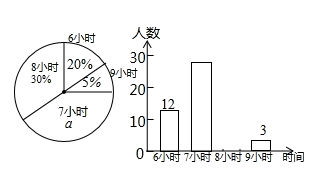
20.(8分)为了了解某校初中各年级学生每天的平均睡眠时间(单位:h,精确到1h),抽样调查了部分学生,并用得到的数据绘制了下面两幅不![]() 完整的统计图.
完整的统计图.
请你根据图中提供的信息,回答下列问题:
(1)求出扇形统计图中百分数a的值为 ,所抽查的学生人数为 .
(2)求出平均睡眠时间为8小时的人数,并补全频数直方图.
(3)求出这部分学生的平均睡眠时间的众数和平均数.
(4)如果该校共有学生1200名,请你估计睡眠不足(少于8小时)的学生数.
21.(10分)某风景区计划在绿化区域种植银杏树,现甲、乙两家有相同的银杏树苗可供选择,其具体销售方案如下:
甲 | 乙 | ||
购树苗数量 | 销售单价 | 购树苗数量 | 销售单价 |
不超过500棵时 | 800元/棵 | 不超过1000棵时 | 800元/棵 |
超过500棵的部分 | 700元/棵 | 超过1000棵的部分 | 600元/棵 |
设购买银杏树苗x棵,到两家购买所需费用分别为y甲元、y乙元
(1)该风景区需要购买800棵银杏树苗,若都在甲家购买所要费用为 元,若都在乙家购买所需费用为 元;
(2)当x>1000时,分别求出y甲、y乙与x之间的函数关系式;
(3)如果你是该风景区的负责人,购买树苗时有什么方案,为什么?
22.(10分)中央电视台的“朗读者”节目激发了同学们的读书热情,为了引导学生“多读书,读好书”,某校对八年级部分学生的课外阅读量进行了随机调查,整理调查结果发现,学生课外阅读的本数最少的有5本,最多的有8本,并根据调查结果绘制了不完整的图表:
本数(本) | 人数(人数) | 百分比 |
5 | a | 0.2 |
6 | 18 | 0.36 |
7 | 14 | b |
8 | 8 | 0.16 |
合计 | c | 1 |
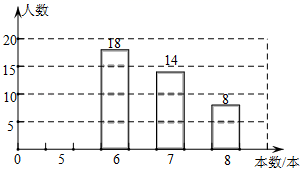
根据以上提供的信息,解答下列问题:
(1)a=_____,b=_____,c=______;
(2)补全上面的条形统计图;
(3)若该校八年级共有1200名学生,请你分析该校八年级学生课外阅读7本及以上的有多少名?
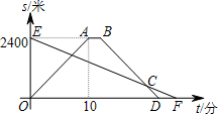
23.(12分)一条笔直的公路上有甲乙两地相距2400米,王明步行从甲地到乙地,每分钟走96米,李越骑车从乙地到甲地后休息2分钟沿原路原速返回乙地.设他们同时出发,运动的时间为t(分),与乙地的距离为s(米),图中线段EF,折线OABD分别表示两人与乙地距离s和运动时间t之间的函数关系图象.
(1)李越骑车的速度为______米/分钟;
(2)B点的坐标为______;
(3)李越从乙地骑往甲地时,s与t之间的函数表达式为______;
(4)王明和李越二人______先到达乙地,先到______分钟.
参考答案
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1、D
2、C
3、A
4、C
5、B
6、C
7、D
8、D
9、B
10、D
11、A
12、B
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13、![]()
14、![]() 且
且![]() .
.
15、10或2![]()
16、![]() .
.
17、![]()
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18、![]()
19、(1)四边形![]() 是菱形,见解析;(2)见解析;(3)黄金矩形
是菱形,见解析;(2)见解析;(3)黄金矩形![]() (或黄金矩形
(或黄金矩形![]() );(4)希腊的巴特农神庙(或巴黎圣母院).
);(4)希腊的巴特农神庙(或巴黎圣母院).
20、(1)45%,60;(2)见解析18;(3)7,7.2;(4)780
21、 (1)610000; 1;(2)当x>1000时,y甲=700x+50000,y乙=600x+200000,x为正整数;(3)当0≤x≤500时或x=1500时,到两家购买所需费用一样;当500<x<1500时,到甲家购买合算;当x>1500时,到乙家购买合算.
22、(1)10,0.28,50;(2)补图见解析;(3)该校八年级学生课外阅读7本及以上的有528名.
23、(1)240;(2)(12,2400);(1)s=240t;(4)李越,1
浙江省宁波市国际学校2023-2024学年八上数学期末质量跟踪监视模拟试题含答案: 这是一份浙江省宁波市国际学校2023-2024学年八上数学期末质量跟踪监视模拟试题含答案,共7页。试卷主要包含了下列各式中,正确的是,比较,3,的大小,正确的是,若分式的值为,则的值为等内容,欢迎下载使用。
浙江省宁波市第七中学2022-2023学年七下数学期末学业质量监测模拟试题含答案: 这是一份浙江省宁波市第七中学2022-2023学年七下数学期末学业质量监测模拟试题含答案,共8页。试卷主要包含了如图,在菱形中,,等内容,欢迎下载使用。
浙江省宁波市慈溪市阳光实验中学2022-2023学年七下数学期末学业质量监测模拟试题含答案: 这是一份浙江省宁波市慈溪市阳光实验中学2022-2023学年七下数学期末学业质量监测模拟试题含答案,共7页。试卷主要包含了如图,点A是反比例函数等内容,欢迎下载使用。












