


浙江省嘉兴市秀洲片区2022-2023学年七下数学期末检测试题含答案
展开
这是一份浙江省嘉兴市秀洲片区2022-2023学年七下数学期末检测试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁,下列命题中,不正确的是,已知数据等内容,欢迎下载使用。
浙江省嘉兴市秀洲片区2022-2023学年七下数学期末检测试题(时间:120分钟 分数:120分) 学校_______ 年级_______ 姓名_______ 考生请注意:1.答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内,不得在试卷上作任何标记。2.第一部分选择题每小题选出答案后,需将答案写在试卷指定的括号内,第二部分非选择题答案写在试卷题目指定的位置上。3.考生必须保证答题卡的整洁。考试结束后,请将本试卷和答题卡一并交回。 一、选择题(每小题3分,共30分)1.为了参加我市组织的“我爱家乡美”系列活动,某校准备从九年级四个班中选出一个班的7名学生组建舞蹈队,要求各班选出的学生身高较为整齐,且平均身高约为1.6m.根据各班选出的学生,测量其身高,计算得到的数据如右表所示,学校应选择( ) 学生平均身高(单位:m)标准差九(1)班1.570.3九(2)班1.570.7九(3)班1.60.3九(4)班1.60.7A.九(1)班 B.九(2)班 C.九(3)班 D.九(4)班2.下列式子从左到右的变形中,属于因式分解的是( )A.10![]() 2-5
2-5![]() =5
=5![]() (2
(2![]() -1) B.
-1) B.![]() (
(![]() +y) =
+y) =![]()
![]() +
+![]() C.
C.![]() 2-4
2-4![]() +4=
+4=![]() (
(![]() -4)+4 D.
-4)+4 D.![]() 2-16+3
2-16+3![]() =(
=(![]() -4)(
-4)(![]() +4)+3
+4)+3![]() 3.如图直线
3.如图直线![]() :
:![]() 与直线
与直线![]() :
:![]() 相交于点P(1,2).则关于x的不等式
相交于点P(1,2).则关于x的不等式![]() 的解集为( )
的解集为( )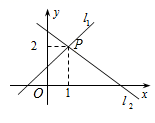 A.x<1 B.x>2 C.x>1 D.x<24.如图,一次函数
A.x<1 B.x>2 C.x>1 D.x<24.如图,一次函数![]() 的图象与两坐标轴分别交于
的图象与两坐标轴分别交于![]() 、
、![]() 两点,点
两点,点![]() 是线段
是线段![]() 上一动点(不与点A、B重合),过点
上一动点(不与点A、B重合),过点![]() 分别作
分别作![]() 、
、![]() 垂直于
垂直于![]() 轴、
轴、![]() 轴于点
轴于点![]() 、
、![]() ,当点
,当点![]() 从点
从点![]() 开始向点
开始向点![]() 运动时,则矩形
运动时,则矩形![]() 的周长( )
的周长( )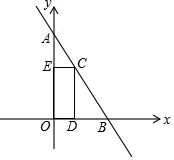 A.不变 B.逐渐变大 C.逐渐变小 D.先变小后变大5.如图,菱形OABC的顶点O是原点,顶点B在y轴上,菱形的两条对角线的长分别是6和4,反比例函数y=
A.不变 B.逐渐变大 C.逐渐变小 D.先变小后变大5.如图,菱形OABC的顶点O是原点,顶点B在y轴上,菱形的两条对角线的长分别是6和4,反比例函数y=![]() (x<0)的图象经过点C,则k的值为( )
(x<0)的图象经过点C,则k的值为( )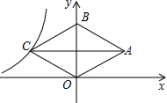 A.24 B.-12 C.-6 D.±66.下列命题中,不正确的是( )A.对角线互相垂直的四边形是菱形 B.正多边形每个内角都相等C.对顶角相等 D.矩形的两条对角线相等7.定义
A.24 B.-12 C.-6 D.±66.下列命题中,不正确的是( )A.对角线互相垂直的四边形是菱形 B.正多边形每个内角都相等C.对顶角相等 D.矩形的两条对角线相等7.定义![]() ,当
,当![]() 时,
时,![]() ,当
,当![]() <
<![]() 时,
时,![]() ;已知函数
;已知函数![]() ,则该函数的最大值是( )A.
,则该函数的最大值是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 8.已知数据:2,﹣1,3,5,6,5,则这组数据的众数和极差分别是( )A.5和7 B.6和7 C.5和3 D.6和39.中国“一带一路”战略沿线国家和地区带来很大的经济效益,沿线某地区居民2017年人均收入为
8.已知数据:2,﹣1,3,5,6,5,则这组数据的众数和极差分别是( )A.5和7 B.6和7 C.5和3 D.6和39.中国“一带一路”战略沿线国家和地区带来很大的经济效益,沿线某地区居民2017年人均收入为![]() 美元,预计2019年人均收入将达到
美元,预计2019年人均收入将达到![]() 美元,设2017年到2019年该地区居民年人均收入平均增长率为
美元,设2017年到2019年该地区居民年人均收入平均增长率为![]() ,可列方程为( )A.
,可列方程为( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 10.下列二次根式中,属于最简二次根式的是
10.下列二次根式中,属于最简二次根式的是![]()
![]() A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 二、填空题(本大题共有6小题,每小题3分,共18分)11.已知m是一元二次方程
二、填空题(本大题共有6小题,每小题3分,共18分)11.已知m是一元二次方程![]() 的一个根 , 则代数式
的一个根 , 则代数式![]() 的值是_____12.八年级(4)班有男生24人,女生16人,从中任选1人恰是男生的事件是_______事件(填“必然”或“不可能”或“随机”).13.一组数据3,2,4,5,2的众数是______.14.直线y=﹣2x﹣1向上平移3个单位,再向左平移2个单位,得到的直线是_____.15.如图,在边长为2的正方形ABCD的外部作
的值是_____12.八年级(4)班有男生24人,女生16人,从中任选1人恰是男生的事件是_______事件(填“必然”或“不可能”或“随机”).13.一组数据3,2,4,5,2的众数是______.14.直线y=﹣2x﹣1向上平移3个单位,再向左平移2个单位,得到的直线是_____.15.如图,在边长为2的正方形ABCD的外部作![]() ,且
,且![]() ,连接DE、BF、BD,则
,连接DE、BF、BD,则![]() ________.
________.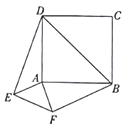 16.如图,DE为Rt△ABC的中位线,点F在DE上,且∠AFB=∠BAC=90°,若AB=4,AC=8,则EF的长为____.(结果保留根号)
16.如图,DE为Rt△ABC的中位线,点F在DE上,且∠AFB=∠BAC=90°,若AB=4,AC=8,则EF的长为____.(结果保留根号)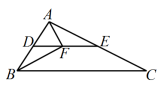 三、解下列各题(本大题共8小题,共72分)17.(8分)如图,在正方形ABCD中,点E为AB上的点(不与A,B重合),△ADE与△FDE关于DE对称,作射线CF,与DE的延长线相交于点G,连接AG,
三、解下列各题(本大题共8小题,共72分)17.(8分)如图,在正方形ABCD中,点E为AB上的点(不与A,B重合),△ADE与△FDE关于DE对称,作射线CF,与DE的延长线相交于点G,连接AG,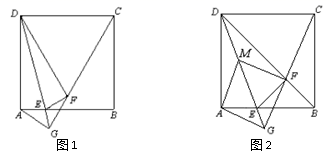 (1)当∠ADE=15°时,求∠DGC的度数;(2)若点E在AB上移动,请你判断∠DGC的度数是否发生变化,若不变化,请证明你的结论;若会发生变化,请说明理由;(3)如图2, 当点F落在对角线BD上时,点M为DE的中点,连接AM,FM,请你判断四边形AGFM的形状,并证明你的结论。 18.(8分)如图,在△ABC中,D是BC边上的一点,已知AB=13,AD=12,AC=11,BD=1.(1)求证:AD⊥BC;(2)求CD的长
(1)当∠ADE=15°时,求∠DGC的度数;(2)若点E在AB上移动,请你判断∠DGC的度数是否发生变化,若不变化,请证明你的结论;若会发生变化,请说明理由;(3)如图2, 当点F落在对角线BD上时,点M为DE的中点,连接AM,FM,请你判断四边形AGFM的形状,并证明你的结论。 18.(8分)如图,在△ABC中,D是BC边上的一点,已知AB=13,AD=12,AC=11,BD=1.(1)求证:AD⊥BC;(2)求CD的长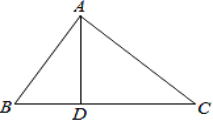 19.(8分)某单位欲从内部招聘管理人员一名,对甲、乙、丙三名候选人进行了笔试和面试两项测试,三人的测试成绩如下表所示:
19.(8分)某单位欲从内部招聘管理人员一名,对甲、乙、丙三名候选人进行了笔试和面试两项测试,三人的测试成绩如下表所示: 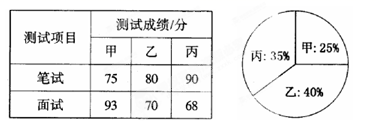 根据录用程序,组织200名职工对三人利用投票推荐的方式进行民主评议,三人得票率(没有弃权票,每位职工只能推荐1人)如上图所示,每得一票记作1分. (l)请算出三人的民主评议得分; (2)如果根据三项测试的平均成绩确定录用人选,那么谁将被录用(精确到 0.01 )? (3)根据实际需要,单位将笔试、面试、民主评议三项测试得分按 4 : 3 : 3 的比例确定个人成绩,那么谁将被录用? 20.(8分)如图,在正方形ABCD中,对角线AC,BD相较于点O,
根据录用程序,组织200名职工对三人利用投票推荐的方式进行民主评议,三人得票率(没有弃权票,每位职工只能推荐1人)如上图所示,每得一票记作1分. (l)请算出三人的民主评议得分; (2)如果根据三项测试的平均成绩确定录用人选,那么谁将被录用(精确到 0.01 )? (3)根据实际需要,单位将笔试、面试、民主评议三项测试得分按 4 : 3 : 3 的比例确定个人成绩,那么谁将被录用? 20.(8分)如图,在正方形ABCD中,对角线AC,BD相较于点O,![]() 的角平分线BF交CD于点E,交AC于点F
的角平分线BF交CD于点E,交AC于点F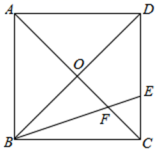
![]() 求证:
求证:![]() ;
;![]() 若
若![]() ,求AB的值 21.(8分)如图,正方形ABCD的对角线交于点O,点E、F分别在AB、BC上(AE<BE),且∠EOF=90°,OE、DA的延长线交于点M,OF、AB的延长线交于点N,连接MN.(1)求证:OM=ON;(2)若正方形ABCD的边长为6,OE=EM,求MN的长.
,求AB的值 21.(8分)如图,正方形ABCD的对角线交于点O,点E、F分别在AB、BC上(AE<BE),且∠EOF=90°,OE、DA的延长线交于点M,OF、AB的延长线交于点N,连接MN.(1)求证:OM=ON;(2)若正方形ABCD的边长为6,OE=EM,求MN的长.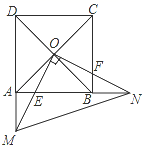 22.(10分)甲、乙两家草莓采摘园的草莓品质相同,销售价格也相同.“五一期间”,两家均推出了优惠方案,甲采摘园的优惠方案是:游客进园需购买50元的门票,采摘的草莓六折优惠;乙采摘园的优惠方案是:游客进园不需购买门票,采摘园的草莓超过一定数量后,超过部分打折优惠.优惠期间,设某游客的草莓采摘量为x(千克),在甲采摘园所需总费用为
22.(10分)甲、乙两家草莓采摘园的草莓品质相同,销售价格也相同.“五一期间”,两家均推出了优惠方案,甲采摘园的优惠方案是:游客进园需购买50元的门票,采摘的草莓六折优惠;乙采摘园的优惠方案是:游客进园不需购买门票,采摘园的草莓超过一定数量后,超过部分打折优惠.优惠期间,设某游客的草莓采摘量为x(千克),在甲采摘园所需总费用为![]() (元),在乙采摘园所需总费用为
(元),在乙采摘园所需总费用为![]() (元),图中折线OAB表示
(元),图中折线OAB表示![]() 与x之间的函数关系.
与x之间的函数关系.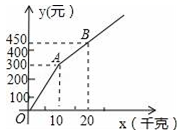 (1)甲、乙两采摘园优惠前的草莓销售价格是每千克 元;(2)求
(1)甲、乙两采摘园优惠前的草莓销售价格是每千克 元;(2)求![]() 、
、![]() 与x的函数表达式;(3)在图中画出
与x的函数表达式;(3)在图中画出![]() 与x的函数图象,并写出选择甲采摘园所需总费用较少时,草莓采摘量x的范围. 23.(10分)如图1,两个全等的直角三角板ABC和DEF重叠在一起,其中∠ACB=∠DFE=90°,∠A=60°,AC=1,固定△ABC,将△DEF沿线段AB向右平移(即点D在线段AB上),回答下列问题:
与x的函数图象,并写出选择甲采摘园所需总费用较少时,草莓采摘量x的范围. 23.(10分)如图1,两个全等的直角三角板ABC和DEF重叠在一起,其中∠ACB=∠DFE=90°,∠A=60°,AC=1,固定△ABC,将△DEF沿线段AB向右平移(即点D在线段AB上),回答下列问题: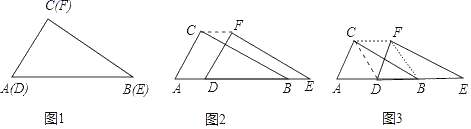 (1)如图2,连结CF,四边形ADFC一定是 形.(2)连接DC,CF,FB,得到四边形CDBF.①如图3,当点D移动到AB的中点时,四边形CDBF是 形.其理由?②在△DEF移动过程中,四边形CDBF的形状在不断改变,但它的面积不变化,其面积为 . 24.(12分)某开发公司生产的960件新产品,需要精加工后,才能投放市场.现有甲、乙两个工厂都想加工这批产品,已知甲工厂单独加工完这批产品比乙工厂单独加工完这批产品多用20天,而乙工厂每天比甲工厂多加工8件产品,公司需付甲工厂加工费用每天80元,乙工厂加工费用每天120元.(1)求甲、乙两个工厂每天各能加工多少件新产品.(2)公司制定产品加工方案如下:可以由每个厂家单独完成;也可以由两个厂家同时合作完成.在加工过程中,公司需派一名工程师每天到厂进行技术指导,并负担每天5元的误餐补助费. 请你帮助公司选择一种既省时又省钱的加工方案,并说明理由. 参考答案 一、选择题(每小题3分,共30分)1、C2、A3、C4、A5、C6、A7、B8、A9、B10、A 二、填空题(本大题共有6小题,每小题3分,共18分)11、
(1)如图2,连结CF,四边形ADFC一定是 形.(2)连接DC,CF,FB,得到四边形CDBF.①如图3,当点D移动到AB的中点时,四边形CDBF是 形.其理由?②在△DEF移动过程中,四边形CDBF的形状在不断改变,但它的面积不变化,其面积为 . 24.(12分)某开发公司生产的960件新产品,需要精加工后,才能投放市场.现有甲、乙两个工厂都想加工这批产品,已知甲工厂单独加工完这批产品比乙工厂单独加工完这批产品多用20天,而乙工厂每天比甲工厂多加工8件产品,公司需付甲工厂加工费用每天80元,乙工厂加工费用每天120元.(1)求甲、乙两个工厂每天各能加工多少件新产品.(2)公司制定产品加工方案如下:可以由每个厂家单独完成;也可以由两个厂家同时合作完成.在加工过程中,公司需派一名工程师每天到厂进行技术指导,并负担每天5元的误餐补助费. 请你帮助公司选择一种既省时又省钱的加工方案,并说明理由. 参考答案 一、选择题(每小题3分,共30分)1、C2、A3、C4、A5、C6、A7、B8、A9、B10、A 二、填空题(本大题共有6小题,每小题3分,共18分)11、![]() .12、随机13、114、y=﹣2x﹣215、116、
.12、随机13、114、y=﹣2x﹣215、116、![]() 三、解下列各题(本大题共8小题,共72分)17、 (1) ∠DGC=45°; (2) ∠DGC=45°不会变化; (3) 四边形AGFM是正方形18、919、 (l) 50 分,80 分,70 分(2)候选人乙将被录用(3)候选人丙将被录用20、(1)详见解析;(2)
三、解下列各题(本大题共8小题,共72分)17、 (1) ∠DGC=45°; (2) ∠DGC=45°不会变化; (3) 四边形AGFM是正方形18、919、 (l) 50 分,80 分,70 分(2)候选人乙将被录用(3)候选人丙将被录用20、(1)详见解析;(2)![]() .21、(1)见解析;(2)MN
.21、(1)见解析;(2)MN![]() .22、(1)1;(2)
.22、(1)1;(2)![]() ,
,![]() ;(3)
;(3)![]() <x<
<x<![]() .23、(1)平行四边;(2)①见解析;②
.23、(1)平行四边;(2)①见解析;②![]() 24、 (1)甲、乙两个工厂每天各能加工16和24件.(2)合作.
24、 (1)甲、乙两个工厂每天各能加工16和24件.(2)合作.
相关试卷
这是一份浙江省嘉兴市秀洲片区2023-2024学年数学九年级第一学期期末质量跟踪监视试题含答案,共7页。试卷主要包含了答题时请按要求用笔,已知点A,点到轴的距离是等内容,欢迎下载使用。
这是一份浙江省嘉兴市秀洲片区2023-2024学年数学八上期末调研试题含答案,共8页。试卷主要包含了如图,直线与的图像交于点等内容,欢迎下载使用。
这是一份浙江省嘉兴市上海外国语大秀洲外国语学校2022-2023学年七下数学期末复习检测模拟试题含答案,共6页。试卷主要包含了在中,若是的正比例函数,则值为,计算的正确结果是等内容,欢迎下载使用。








