


河南省洛阳市东方二中学2022-2023学年数学七下期末质量跟踪监视试题含答案
展开河南省洛阳市东方二中学2022-2023学年数学七下期末质量跟踪监视试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
考生请注意:
1.答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内,不得在试卷上作任何标记。
2.第一部分选择题每小题选出答案后,需将答案写在试卷指定的括号内,第二部分非选择题答案写在试卷题目指定的位置上。
3.考生必须保证答题卡的整洁。考试结束后,请将本试卷和答题卡一并交回。
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知![]() ,
,![]() ,
,![]() 是反比例函数
是反比例函数![]() 的图象上的三点,且
的图象上的三点,且![]() ,则
,则![]() 、
、![]() 、
、![]() 的大小关系是( )
的大小关系是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.如图,在△ABC中,AB=3,AC=4,BC=5,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,则EF的最小值为( )
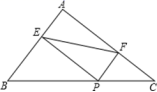
A.2 B.2.2 C.2.4 D.2.5
3.我市四月份某一周每天的最高气温(单位:℃)统计如下:29,30,25,27,25,则这组数据的中位数与众数分别是( )
A.25;25 B.29;25 C.27;25 D.28;25
4.如图,在菱形![]() 中,
中,![]() =120°,点E是边
=120°,点E是边![]() 的中点,P是对角线
的中点,P是对角线![]() 上的一个动点,若AB=2,则PB+PE的最小值是( )
上的一个动点,若AB=2,则PB+PE的最小值是( )
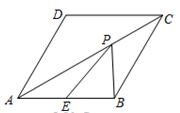
A.1 B.![]() C.2 D.
C.2 D.![]()
5.赵老师是一名健步走运动的爱好者为备战2019中国地马拉松系列赛·广元站10千米群众健身赛,她用手机软件记录了某个月(30天)每天健步走的步数(单位:万步),将记录结果绘制成了如图所示的统计图在每天健步走的步数这组数据中,众数和中位数分别是( )

A.2.2,2.3 B.2.4,2.3 C.2.4,2.35 D.2.3,2.3
6.关于x的方程![]() =0有增根,则m的值是( )
=0有增根,则m的值是( )
A.2 B.﹣2 C.1 D.﹣1
7.已知直角三角形的两直角边长分别为5和12,则此直角三角形斜边上的中线长为()
A.![]() B.6 C.13 D.
B.6 C.13 D.![]()
8.下列命题是假命题的是( )
A.四个角相等的四边形是矩形 B.对角线互相平分的四边形是平行四边形
C.四条边相等的四边形是菱形 D.对角线互相垂直且相等的四边形是正方形
9.若一次函数![]() 不经过第三象限,则
不经过第三象限,则![]() 的取值范围为
的取值范围为
A.![]() B.
B.![]()
C.![]() D.
D.![]()
10.下列说法正确的是( )
A.全等的两个图形成中心对称
B.成中心对称的两个图形必须能完全重合
C.旋转后能重合的两个图形成中心对称
D.成中心对称的两个图形不一定全等
11.下列说法正确的是( )
A.若你在上一个路口遇到绿灯,则在下一路口必遇到红灯
B.某蓝球运动员2次罚球,投中一个,则可断定他罚球命中的概率一定为50%
C.“明天我市会下雨”是随机事件
D.若某种彩票中奖的概率是1%,则买100张该种彩票一定会中奖
12.如图,在矩形![]() 中,对角线
中,对角线![]() ,
,![]() 交于点
交于点![]() ,已知
,已知![]() ,
,![]() ,则
,则![]() 的长为( )
的长为( )
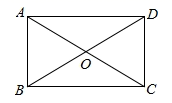
A.2 B.4 C.6 D.8
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13.关于x的不等式组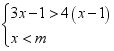 的解集为x<3,那么m的取值范围是_____.
的解集为x<3,那么m的取值范围是_____.
14.计算: ![]() =_________.
=_________.
15.在4个不透明的袋子中分别装有10个球,其中,1号袋中有10个红球,2号袋中有8个红球.2个白球,3号袋中有5个红球.5个白球,4号袋中有2个红球,8个白球.从各个袋子中任意摸出1个球,摸到白球的可能性最大的是_____(填袋子号).
16.中国“一带一路”战略给沿线国家和地区带来很大的经济效益,沿线某地区居民2017年人均收入![]() 美元,预计2019年人均收入将达到
美元,预计2019年人均收入将达到![]() 美元,设2017年到2019年该地区人均收入平均增长率为
美元,设2017年到2019年该地区人均收入平均增长率为![]() ,可列方程为__________.
,可列方程为__________.
17.对于实数![]() ,
,![]() ,
,![]() ,
,![]() 表示
表示![]() ,
,![]() 两数中较小的数,如
两数中较小的数,如![]() ,
,![]() .若关于
.若关于![]() 的函数
的函数![]() ,
,![]() 的图象关于直线
的图象关于直线![]() 对称,则
对称,则![]() 的取值范围是__,对应的
的取值范围是__,对应的![]() 值是__.
值是__.
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18.(5分)已知直线![]() 分别交x轴于点A、交y轴于点
分别交x轴于点A、交y轴于点![]()
![]() 求该直线的函数表达式;
求该直线的函数表达式;
![]() 求线段AB的长.
求线段AB的长.
19.(5分)先化简,再求值:(x+2+![]() )÷
)÷![]() ,其中x=2
,其中x=2![]() .
.
20.(8分)(1) [探索发现]正方形![]() 中,
中,![]() 是对角线
是对角线![]() 上的一个动点(与点
上的一个动点(与点![]() 不重合),过点
不重合),过点![]() 作
作![]() 交线段
交线段![]() 于点
于点![]() .求证:
.求证: ![]()
小玲想到的思路是:过点![]() 作
作![]() 于点
于点![]() 于点
于点![]() ,通过证明
,通过证明![]() 得到
得到![]() .请按小玲的思路写出证明过程
.请按小玲的思路写出证明过程
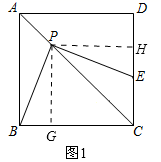
(2)[应用拓展]如图2,在![]() 的条件下,设正方形
的条件下,设正方形![]() 的边长为
的边长为![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() .求
.求![]() 的长.
的长.
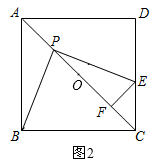
21.(10分)(1)因式分解:![]()
(2)解方程:![]()
22.(10分)某校为了了解八年级学生的身体素质情况,该校体育老师从八年级学生中随机抽取了50名进行一分钟跳绳次数测试,以测试数据为样本,绘制了如下的统计图表:
组别 | 次数 | 频数(人数) |
第1组 |
| 6 |
第2组 |
| 8 |
第3组 |
|
|
第4组 |
| 18 |
第5组 |
| 6 |
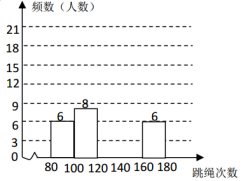
请结合图表完成下列问题:
(1)表中的![]() ______ ;
______ ;
(2)请把频数分布直方图补充完整;
(3)所抽取的50名学生跳绳成绩的中位数落在哪一组?
(4)该校八年级学生共有500人,若规定一分钟跳绳次数(![]() )在
)在![]() 时为达标,请估计该校八年级学生一分钟跳绳有多少人达标?
时为达标,请估计该校八年级学生一分钟跳绳有多少人达标?
23.(12分)几何学的产生,源于人们对土地面积测量的需要,以面积早就成为人们认识图形性质与几何证明的有效工具,可以说几何学从一开始便与面积结下了不解之缘.我们已经掌握了平行四边形面积的求法,但是一般四边形的面积往往不易求得,那么我们能否将其转化为平行四边形来求呢?
(1)方法1:如图①,连接四边形![]() 的对角线
的对角线![]() ,
,![]() ,分别过四边形
,分别过四边形![]() 的四个顶点作对角线的平行线,所作四条线相交形成四边形
的四个顶点作对角线的平行线,所作四条线相交形成四边形![]() ,易证四边形
,易证四边形![]() 是平行四边形.请直接写出S四边形ABCD和
是平行四边形.请直接写出S四边形ABCD和![]() 之间的关系:_______________.
之间的关系:_______________.
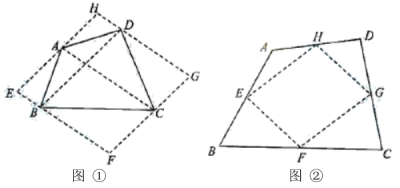
方法2:如图②,取四边形![]() 四边的中点
四边的中点![]() ,
,![]() ,
,![]() ,
,![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,
,![]() ,
,
(2)求证:四边形![]() 是平行四边形;
是平行四边形;
(3)请直接写出S四边形ABCD与![]() 之间的关系:_____________.
之间的关系:_____________.
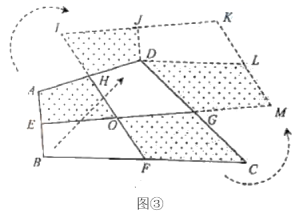
方法3:如图③,取四边形![]() 四边的中点
四边的中点![]() ,
,![]() ,
,![]() ,
,![]() ,连接
,连接![]() ,
,![]() 交于点
交于点![]() .先将四边形
.先将四边形![]() 绕点
绕点![]() 旋转
旋转![]() 得到四边形
得到四边形![]() ,易得点
,易得点![]() ,
,![]() ,
,![]() 在同一直线上;再将四边形
在同一直线上;再将四边形![]() 绕点
绕点![]() 旋转
旋转![]() 得到四边形
得到四边形![]() ,易得点
,易得点![]() ,
,![]() ,
,![]() 在同一直线上;最后将四边形
在同一直线上;最后将四边形![]() 沿
沿![]() 方向平移,使点
方向平移,使点![]() 与点
与点![]() 重合,得到四边形
重合,得到四边形![]() ;
;
(4)由旋转、平移可得![]() _________,
_________,![]() _________,所以
_________,所以![]() ,所以点
,所以点![]() ,
,![]() ,
,![]() 在同一直线上,同理,点
在同一直线上,同理,点![]() ,
,![]() ,
,![]() 也在同一点线上,所以我们拼接成的图形是一个四边形.
也在同一点线上,所以我们拼接成的图形是一个四边形.
(5)求证:四边形![]() 是平行四边形.
是平行四边形.
(注意:请考生在下面2题中任选一题作答如果多做,则按所做的第一题计分)
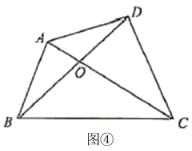
(6)应用1:如图④,在四边形![]() 中,对角线
中,对角线![]() 与
与![]() 交于点
交于点![]() ,
,![]() ,
,![]() ,
,![]() ,则S四边形ABCD=
,则S四边形ABCD= ![]() .
.
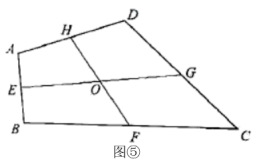
(7)应用2:如图⑤,在四边形![]() 中,点
中,点![]() ,
,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() ,
,![]() ,
,![]() 的中点,连接
的中点,连接![]() ,
,![]() 交于点
交于点![]() ,
,![]() ,
,![]() ,
,![]() ,则S四边形ABCD=___________
,则S四边形ABCD=___________![]()
参考答案
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1、C
2、C
3、C
4、B
5、B
6、A
7、D
8、D
9、A
10、B
11、C
12、B
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13、m≥1
14、![]()
15、1
16、![]()
17、![]() 或
或![]() , 6或3.
, 6或3.
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18、(1)![]() ;(2)AB=
;(2)AB=![]() .
.
19、![]() ,4-2
,4-2![]() .
.
20、(1)详见解析;(2)![]()
21、(1)![]() ,(2)
,(2)![]()
22、(1)12;(2)见解析;(3)第3组;(4)360人;
23、(1)S四边形ABCD![]() ;(2)见详解;(1)S四边形ABCD
;(2)见详解;(1)S四边形ABCD ![]() ;(4)AEO,OEB;(5)见详解;(6)
;(4)AEO,OEB;(5)见详解;(6)![]() ;(7)
;(7)![]()
2023-2024学年河南省洛阳市东方第二中学数学九上期末质量跟踪监视试题含答案: 这是一份2023-2024学年河南省洛阳市东方第二中学数学九上期末质量跟踪监视试题含答案,共9页。试卷主要包含了答题时请按要求用笔等内容,欢迎下载使用。
安徽宣城古泉中学2022-2023学年数学七下期末质量跟踪监视试题含答案: 这是一份安徽宣城古泉中学2022-2023学年数学七下期末质量跟踪监视试题含答案,共7页。试卷主要包含了答题时请按要求用笔,如图,直线y=ax+b过点A等内容,欢迎下载使用。
2022-2023学年黄冈中学数学七下期末质量跟踪监视模拟试题含答案: 这是一份2022-2023学年黄冈中学数学七下期末质量跟踪监视模拟试题含答案,共8页。试卷主要包含了答题时请按要求用笔,下列各式中,最简二次根式为等内容,欢迎下载使用。












