江苏省盐城市东台第一教育集团2022-2023学年数学七下期末经典模拟试题含答案

江苏省盐城市东台第一教育集团2022-2023学年数学七下期末经典模拟试题

（时间：120分钟             分数：120分）

学校_______            年级_______        姓名_______

注意事项:

1．答题前，考生先将自己的姓名、准考证号码填写清楚，将条形码准确粘贴在条形码区域内。

2．答题时请按要求用笔。

3．请按照题号顺序在答题卡各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试卷上答题无效。

4．作图可先使用铅笔画出，确定后必须用黑色字迹的签字笔描黑。

5．保持卡面清洁，不要折暴、不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。

一、选择题(每小题3分,共30分)

1．已知正比例函数y＝﹣2x的图象经过点（a，2），则a的值为（　　）

A． B．﹣1 C．﹣ D．﹣4

2．甲、乙、丙、丁四位选手各射击10次，每人的平均成绩都是9.3环，方差如下表所示：

则这四人中成绩最稳定的是（    ）

A．甲 B．乙 C．丙 D．丁

3．函数中自变量的取值范围是（    ）

A． B． C．且 D．且

4．如图， OABC的顶点O，A，C的坐标分别是（0，0），（2，0），（，1），则点B的坐标是（    ）

A．（1，2） B．（，2） C．（，1） D．（3，1）

5．用反证法证明“”，应假设（    ）

A． B． C． D．

6．用配方法解关于的一元二次方程，配方后的方程可以是（    ）

A． B．

C． D．

7．宁宁所在的班级有42人，某次考试他的成绩是80分，若全班同学的平均分是78分，判断宁宁成绩是否在班级属于中等偏上，还需要了解班级成绩的（    ）

A．中位数 B．众数 C．加权平均数 D．方差

8．如图，在矩形纸片中，，，将纸片折叠，使点落在边上的点处，折痕为，再将沿向右折叠，点落在点处，与交于点，则的面积为（    ）

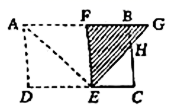
A．4 B．6 C．8 D．10

9．设0＜k＜2，关于x的一次函数y=kx+2（1-x），当1≤x≤2时的最大值是（　　）

A．2k-2    B．k-1    C．k    D．k+1

10．对于一次函数，如果随的增大而减小，那么反比例函数满足（    ）

A．当时， B．在每个象限内，随的增大而减小

C．图像分布在第一、三象限 D．图像分布在第二、四象限

二、填空题(本大题共有6小题，每小题3分，共18分)

11．计算：_______．

12．如果最简二次根式和是同类二次根式，那么a=_______

13．请写出一个比2小的无理数是___．

14．甲、乙、丙、丁四人进行射击测试，每人10次射击成绩平均数均是9.2环，方差分别为，，，，则成绩最稳定的是______．

15．将直线y＝2x+3向下平移2个单位，得直线_____．

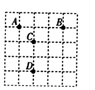
16．如图，在的边长为1的小正方形组成的网格中，格点上有四个点，若要求连接两个点所成线段的长度大于3且小于4，则可以连接__________________.(写出一个答案即可)

三、解下列各题(本大题共8小题，共72分)

17．（8分）某产品每件成本10元，试销阶段每件产品的销售价x（元）与产品的日销量y（件）之间的关系如下表：若日销量y是销售价x的一次函数．

（1）求出日销量y（件）与销售价x（元）的函数关系式；

（2）求销售定价为30元时，每日的销售利润．

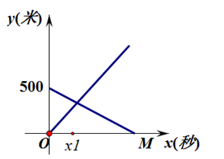
18．（8分）一条笔直跑道上的A，B两处相距500米，甲从A处，乙从B处，两人同时相向匀速而跑，直到乙到达A处时停止，且甲的速度比乙大．甲、乙到A处的距离（米）与跑动时间（秒）的函数关系如图14所示．

（1）若点M的坐标（100，0），求乙从B处跑到A处的过程中与的函数解析式；

（2）若两人之间的距离不超过200米的时间持续了40秒．

①当时，两人相距200米，请在图14中画出P（，0）．保留画图痕迹，并写出画图步骤；

②请判断起跑后分钟，两人之间的距离能否超过420米，并说明理由．

19．（8分）已知正方形中，为对角线上一点，过点作交于点，连接，为的中点，连接．

（1）如图1，求证：；

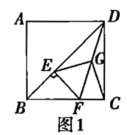
（2）将图1中的绕点逆时针旋转45°，如图2，取的中点，连接．问（1）中的结论是否仍然成立？若成立，给出证明；若不成立，请说明理由．

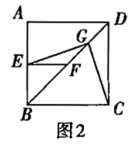
（3）将图1中的绕点逆时计旋转任意角度，如图3，取的中点，连接．问（1）中的结论是否仍然成立？通过观察你还能得出什么结论？（均不要求证明）

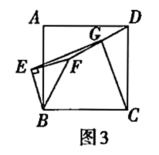
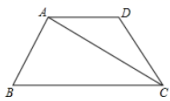
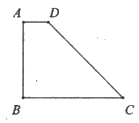
20．（8分）如图，在梯形ABCD中，AD∥BC，AB＝AD＝DC，∠B＝60．

（1）求证：ABAC；

（2）若DC＝2，求梯形ABCD的面积．

21．（8分）（定义学习）

定义:如果四边形有一组对角为直角，那么我们称这样的四边形为“对直四边形”

（判断尝试）

在①梯形;②矩形:③菱形中，是“对直四边形”的是哪一个. (填序号)

（操作探究）

在菱形ABCD中，于点E,请在边AD和CD上各找一点F,使得以点A、E、C、F组成的四边形为“对直四边形”，画出示意图，并直接写出EF的长，

（实践应用）

某加工厂有一批四边形板材，形状如图所示，若AB=3米，AD=1米，

.现根据客户要求，需将每张四边形板材进一步分割成两个等腰三角形板材和一个“对直四边形"板材，且这两个等腰三角形的腰长相等，要求材料充分利用无剩余.求分割后得到的等腰三角形的腰长，

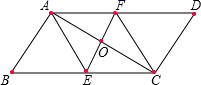
22．（10分）（问题原型）如图，在中，对角线的垂直平分线交于点，交于点，交于点.求证：四边形是菱形.

（小海的证法）证明：

是的垂直平分线，

，（第一步）

，（第二步）

.（第三步）

四边形是平行四边形.（第四步）

四边形是菱形.  （第五步）

（老师评析）小海利用对角线互相平分证明了四边形是平行四边形，再利用对角线互相垂直证明它是菱形，可惜有一步错了.

（挑错改错）（1）小海的证明过程在第________步上开始出现了错误.

（2）请你根据小海的证题思路写出此题的正确解答过程，

23．（10分）如图：矩形ABCD中，AB=2，BC=5，E、P分别在AD、BC上，且DE=BP=1．

（1）判断△BEC的形状，并说明理由？

（2）判断四边形EFPH是什么特殊四边形？并证明你的判断；

（3）求四边形EFPH的面积．

24．（12分）在正方形ABCD 中，点F是BC延长线上一点，过点B作BE⊥DF于点E，交CD于点G，连接CE.

（1）若正方形ABCD边长为3，DF=4，求CG的长；

（2）求证：EF+EG=CE.

参考答案

一、选择题(每小题3分,共30分)

1、B

2、D

3、B

4、C

5、D

6、A

7、A

8、C

9、C

10、D

二、填空题(本大题共有6小题，每小题3分，共18分)

11、2

12、3

13、（答案不唯一）．

14、甲

15、y=2x+1．

16、或

三、解下列各题(本大题共8小题，共72分)

17、 (1) y＝﹣x+1;(2)200元

18、（1）；（2）①见解析；②起跑后分钟，两人之间的距离不能超过米，理由见解析．

19、 (1)见解析;(2)见解析;(3)见解析.

20、（1）见解析；（2）

21、

22、（1）二; （2）见解析.

23、（1）△BEC是直角三角形，理由见解析（2）四边形EFPH为矩形，理由见解析（3）

24、 (1)；(2)证明见解析.