


江苏省海安县2022-2023学年七下数学期末综合测试模拟试题含答案
展开江苏省海安县2022-2023学年七下数学期末综合测试模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
请考生注意:
1.请用2B铅笔将选择题答案涂填在答题纸相应位置上,请用0.5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。
2.答题前,认真阅读答题纸上的《注意事项》,按规定答题。
一、选择题(每小题3分,共30分)
1.运用分式基本性质,等式中![]() 缺少的分子为( )
缺少的分子为( )
A.a B.2a C.3a D.4a
2.在直角坐标系中,将点(﹣2,3)关于原点的对称点向左平移2个单位长度得到的点的坐标是( )
A.(4,﹣3) B.(﹣4,3) C.(0,﹣3) D.(0,3)
3.若点P(-2,a)在第二象限,则a的值可以是( )
A.1 B.-1 C.0 D.-2
4.实数k、b满足kb﹥0,不等式kx<b的解集是![]() 那么函数y=kx+b的图象可能是( )
那么函数y=kx+b的图象可能是( )
A.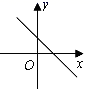 B.
B.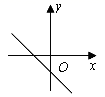 C.
C.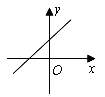 D.
D.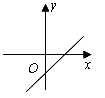
5.方程![]() 的根的情况是( )
的根的情况是( )
A.有两个不相等的实数根 B.有两个相等的实数根 C.无实数根 D.只有一个实数根
6.数据按从小到大排列为1,2,4,x,6,9,这组数据的中位数为5,那么这组数据的众数是( )
A.4 B.5 C.5.5 D.6
7.如图,![]() 中,
中,![]() 于点
于点![]() ,点
,点![]() 为
为![]() 的中点,连接
的中点,连接![]() ,则
,则![]() 的周长是( )
的周长是( )
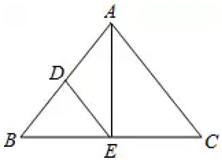
A.4+2![]() B.7+
B.7+![]() C.12 D.10
C.12 D.10
8.某体育馆准备重新铺设地面,已有一部分正三角形的地砖,现要购买另一种不同形状的正多边形地砖与正三角形在同一顶点处作平面镶嵌(正多边形的边长相等),则该体育馆不应该购买的地砖形状是( )
A.正方形 B.正六边形 C.正八边形 D.正十二边形
9.在 2008 年的一次抗震救灾大型募捐活动中,文艺工作者积极向灾区捐款.其中 10 人 的捐款分别是:5 万,8 万,10 万,10 万,10 万,20 万,20 万,30 万,50 万,100 万.这组数据的众数和中位数分别是( )
A.10 万,15 万 B.10 万,20 万 C.20 万,15 万 D.20 万,10 万
10.如图,阴影部分为一个正方形,此正方形的面积是( )\
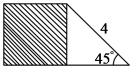
A.2 B.4 C.6 D.8
二、填空题(本大题共有6小题,每小题3分,共18分)
11.某种药品原价75元盒,经过连续两次降价后售价为45元/盒.设平均每次降价的百分率为x,根据题意可列方程为_____.
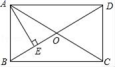
12.如图,在矩形ABCD中,对角线AC,BD相交于点O,AO=3,AE垂直平分OB于点E,则AD的长为_____.
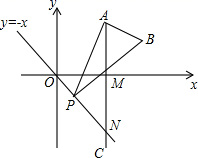
13.如图,已知点A是第一象限内横坐标为![]() 的一个定点,AC⊥x轴于点M,交直线y=﹣x于点N.若点P是线段ON上的一个动点,∠APB=30°,BA⊥PA,则点P在线段ON上运动时,A点不变,B点随之运动.求当点P从点O运动到点N时,点B运动的路径长是_____.
的一个定点,AC⊥x轴于点M,交直线y=﹣x于点N.若点P是线段ON上的一个动点,∠APB=30°,BA⊥PA,则点P在线段ON上运动时,A点不变,B点随之运动.求当点P从点O运动到点N时,点B运动的路径长是_____.
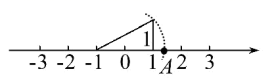
14.如图所示,数轴上点A所表示的数为____.
15.若关于![]() 的一元一次不等式组
的一元一次不等式组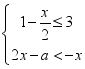 所有整数解的和为-9,且关于
所有整数解的和为-9,且关于![]() 的分式方程
的分式方程![]() 有整数解,则符合条件的所有整数
有整数解,则符合条件的所有整数![]() 为__________.
为__________.
16.已知菱形有一个锐角为60°,一条对角线长为4cm,则其面积为_______ cm1.
三、解下列各题(本大题共8小题,共72分)
17.(8分)中国古代有着辉煌的数学成就,《周牌算经》、《九章算术》、《海岛算经》、《孙子算经》等是我国古代数学的重要文献.
(1)小聪想从这4部数学名著中随机选择1部阅读,求他选中《九章算术》的概率;
(2)小聪拟从这4部数学名著中选择2部作为假课外拓展学习内容,用列表或树状图求选中的名著恰好是《九章算术》和《周牌算经》的概率.
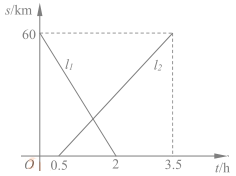
18.(8分)A、B两地相距60km,甲、乙两人从两地出发相向而行,甲先出发.图中![]() 表示两人离A地的距离S(km)与时间t(h)的关系,结合图像回答下列问题:
表示两人离A地的距离S(km)与时间t(h)的关系,结合图像回答下列问题:
(1)表示乙离开A地的距离与时间关系的图像是________(填![]() );
);
甲的速度是__________km/h;乙的速度是________km/h.
(2)甲出发后多少时间两人恰好相距5km?
19.(8分)1号探测气球从海拔5m处出发,以1m/min的速度上升.与此同时,2号探测气球从海拔15m处出发,以0.5m/min的速度上升.两个气球都匀速上升了50min.设气球上升时间为x(x≥0).
(Ⅰ)根据题意,填写下表
上升时间/min | 10 | 30 | … | x |
1号探测气球所在位置的海拔/m | 15 |
| … |
|
2号探测气球所在位置的海拔/m |
| 30 | … |
|
(Ⅱ)在某时刻两个气球能否位于同一高度?如果能,这时气球上升了多长时间?位于什么高度?如果不能,请说明理由.
(Ⅲ)当0≤x≤50时,两个气球所在位置的海拔最多相差多少米?
20.(8分)为了对学生进行多元化的评价,某中学决定对学生进行综合素质评价![]() 设该校中学生综合素质评价成绩为x分,满分为100分评价等级与评价成绩x分之间的关系如下表:
设该校中学生综合素质评价成绩为x分,满分为100分评价等级与评价成绩x分之间的关系如下表:
中学生综合素质评价成绩 | 中学生综合素质评价等级 |
| A级 |
| B级 |
| C级 |
| D级 |
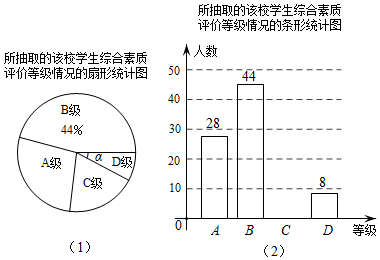
现随机抽取该校部分学生的综合素质评价成绩,整理绘制成图![]() 、图
、图![]() 两幅不完整的统计图
两幅不完整的统计图![]() 请根据相关信息,解答下列问题:
请根据相关信息,解答下列问题:
(1)在这次调查中,一共抽取了______名学生,图![]() 中等级为D级的扇形的圆心角
中等级为D级的扇形的圆心角![]() 等于______
等于______![]() ;
;
(2)补全图![]() 中的条形统计图;
中的条形统计图;
(3)若该校共有1200名学生,请你估计该校等级为C级的学生约有多少名.
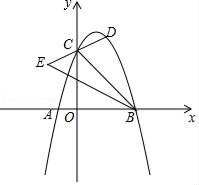
21.(8分)如图,抛物线y=﹣x2+bx+c(a≠0)与x轴交于点A(﹣1,0)和B(3,0),与y轴交于点C,点D的横坐标为m(0<m<3),连结DC并延长至E,使得CE=CD,连结BE,BC.
(1)求抛物线的解析式;
(2)用含m的代数式表示点E的坐标,并求出点E纵坐标的范围;
(3)求△BCE的面积最大值.
22.(10分)某文具店从市场得知如下信息:
| A品牌计算器 | B品牌计算器 |
进价(元/台) | 70 | 100 |
售价(元/台) | 90 | 140 |
该文具店计划一次性购进这两种品牌计算器共50台,设该经销商购进A品牌计算器x台,这两种品牌计算器全部销售完后获得利润为y元.
(1)求y与x之间的函数关系式;
(2)若全部销售完后,获得的利润为1200元,则购进A、B两种品牌计算器的数量各是多少台?
(3)若购进计算器的资金不超过4100元,求该文具店可获得的最大利润是多少元?
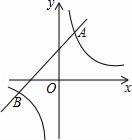
23.(10分)已知一次函数y1=kx+b(k≠0)与反比例函数y2=![]() (m≠0)相交于A和B两点,且A点坐标为(1,1),B点的横坐标为﹣1.
(m≠0)相交于A和B两点,且A点坐标为(1,1),B点的横坐标为﹣1.
(1)求反比例函数和一次函数的解析式;
(2)根据图象直接写出使得y1>y2时,x的取值范围.
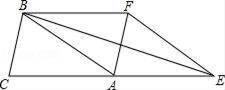
24.(12分)如图,已知△ABC的面积为3,且AB=AC,现将△ABC沿CA方向平移CA长度得到△EFA.
(1)求四边形CEFB的面积;
(2)试判断AF与BE的位置关系,并说明理由;
(3)若∠BEC=15°,求AC的长.
参考答案
一、选择题(每小题3分,共30分)
1、D
2、C
3、A
4、B
5、C
6、D
7、D
8、C
9、A
10、D
二、填空题(本大题共有6小题,每小题3分,共18分)
11、![]()
12、3![]()
13、![]() .
.
14、![]()
15、-4,-1.
16、![]() 或
或 ![]()
三、解下列各题(本大题共8小题,共72分)
17、(1)![]() ;(2)
;(2)![]() .
.
18、(1)![]() ; 30; 20;(2)甲出发后1.3h或者1.5h时,甲乙相距5km.
; 30; 20;(2)甲出发后1.3h或者1.5h时,甲乙相距5km.
19、 (1)35;![]() ;30;
;30;![]() ;(2)此时气球上升了20min,都位于海拔25m的高度;(3)当
;(2)此时气球上升了20min,都位于海拔25m的高度;(3)当![]() 时,y最大值为15.
时,y最大值为15.
20、(1)100;![]() ;(2)补图见解析;(3)240人.
;(2)补图见解析;(3)240人.
21、(1)y=﹣x2+2x+1.(2)2≤Ey<2.(1)当m=1.5时,S△BCE有最大值,S△BCE的最大值=![]() .
.
22、(1)y与x之间的函数关系式为y=2000﹣20x;(2)购进A种品牌计算器的数量是40台,购进A种品牌计算器的数量是10台;(3)该文具店可获得的最大利润是1400元.
23、(1)y1=x+2,y2=![]() ;(2)由图象可知y1>y2时,x>1或﹣1<x<2.
;(2)由图象可知y1>y2时,x>1或﹣1<x<2.
24、(1)9;(2)BE⊥AF,理由详见解析;(3)![]() ;
;
江苏省海安县2023-2024学年数学九上期末检测模拟试题含答案: 这是一份江苏省海安县2023-2024学年数学九上期末检测模拟试题含答案,共7页。试卷主要包含了在比例尺为1,抛物线的顶点坐标是等内容,欢迎下载使用。
江苏省海安县城南实验中学2022-2023学年数学七下期末复习检测模拟试题含答案: 这是一份江苏省海安县城南实验中学2022-2023学年数学七下期末复习检测模拟试题含答案,共7页。试卷主要包含了答题时请按要求用笔,要使式子有意义,则的取值范围是,下列函数,两组数据等内容,欢迎下载使用。
2022-2023学年江苏省镇江市句容市数学七下期末综合测试模拟试题含答案: 这是一份2022-2023学年江苏省镇江市句容市数学七下期末综合测试模拟试题含答案,共7页。试卷主要包含了如图,丝带重叠的部分一定是等内容,欢迎下载使用。












