


江苏无锡梁溪区四校联考2022-2023学年数学七年级第二学期期末调研试题含答案
展开江苏无锡梁溪区四校联考2022-2023学年数学七年级第二学期期末调研试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号、考场号和座位号填写在试题卷和答题卡上。用2B铅笔将试卷类型(B)填涂在答题卡相应位置上。将条形码粘贴在答题卡右上角"条形码粘贴处"。
2.作答选择题时,选出每小题答案后,用2B铅笔把答题卡上对应题目选项的答案信息点涂黑;如需改动,用橡皮擦干净后,再选涂其他答案。答案不能答在试题卷上。
3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新答案;不准使用铅笔和涂改液。不按以上要求作答无效。
4.考生必须保证答题卡的整洁。考试结束后,请将本试卷和答题卡一并交回。
一、选择题(每小题3分,共30分)
1.某商品的价格为![]() 元,连续两次降
元,连续两次降![]() 后的价格是
后的价格是![]() 元,则
元,则![]() 为( )
为( )
A.9 B.10 C.19 D.8
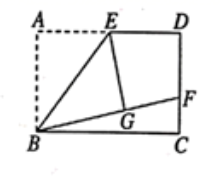
2.如图,矩形ABCD中, E是AD的中点,将![]() 沿直线BE折叠后得到
沿直线BE折叠后得到![]() ,延长BG交CD于点F若
,延长BG交CD于点F若![]() , 则FD的长为( )
, 则FD的长为( )
A.3 B.![]() C.
C.![]() D.
D.![]()
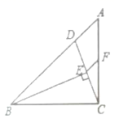
3.如图,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 上一点,
上一点,![]() ,
,![]() 于点
于点![]() ,点
,点![]() 为
为![]() 的中点,连接
的中点,连接![]() ,则
,则![]() 的长为( )
的长为( )
A.5 B.4 C.3 D.2
4.故宫是世界上现存规模最大,保存最完整的宫殿建筑群.下图是利用平面直角坐标系画出的故宫的主要建筑分布示意图.在图中,分别以正东、正北方向为x轴、y轴的正方向,建立平面直角坐标系,有如下四个结论:
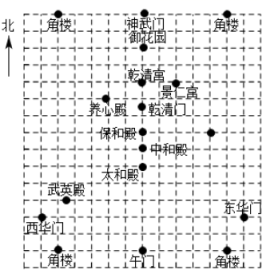
①当表示太和殿的点的坐标为(0,0),表示养心殿的点的坐标为(-2,4)时,表示景仁宫的点的坐标为(2,5);
②当表示太和殿的点的坐标为(0,0),表示养心殿的点的坐标为(-1,2)时,表示景仁宫的点的坐标为(1,3);
③当表示太和殿的点的坐标为(4,-8),表示养心殿的点的坐标为(0,0)时,表示景仁宫的点的坐标为(8,1);
④当表示太和殿的点的坐标为(0,1),表示养心殿的点的坐标为(-2,5)时,表示景仁宫的点的坐标为(2,6).上述结论中,所有正确结论的序号是( )
A.①② B.①③ C.①④ D.②③
5.在平面直角坐标系中,线段AB两端点的坐标分别为A(1,0),B(3,2).将线段AB平移后,A、B的对应点的坐标可以是( )
A.(1,−1),(−1,−3) B.(1,1),(3,3) C.(−1,3),(3,1) D.(3,2),(1,4)
6.在数学活动课上,老师要求同学们判断一个四边形门框是否为矩形,下面是某合作学习小组的四位同学拟定的方案,其中正确的是( )
A.测量对角线是否相互平分 B.测量两组对边是否分别相等
C.测量一组对角是否都为直角 D.测量四边形其中的三个角是否都为直角
7.方程x(x-2)=0的根是( )
A.x=0 B.x=2 C.x1=0,x2=2 D.x1=0,x2=-2
8.化简(-1)2-(-3)0+![]() 得( )
得( )
A.0 B.-2 C.1 D.2
9.下列方程中,是分式方程的为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.如图,在矩形ABCD中,AB=8,AD=6,过点D作直线m∥AC,点E、F是直线m上两个动点,在运动过程中EF∥AC且EF=AC,四边形ACFE的面积是( )
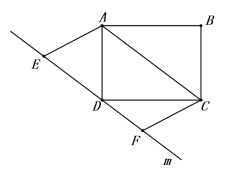
A.48 B.40 C.24 D.30
二、填空题(本大题共有6小题,每小题3分,共18分)
11.廖老师为了了解学生周末利用网络进行学习的时间,在所任教班级随机调查了10名学生,其统计数据如下表:
时间(单位:小时) | 4 | 3 | 2 | l | 0 |
人数 | 3 | 4 | 1 | 1 | 1 |
则这10名学生周末利用网络进行学习的平均时间是________小时.
12.某班七个兴趣小组人数分别为4,x,5,5,4,6,7,已知这组数据的平均数是5,则x=________.
13.如图,四边形ABCD是矩形,对角线AC、BD相交于点O,如果再添加一个条件,即可推出该四边形是正方形,这个条件可以是_________.

14.如图,在菱形ABCD中,AC、BD交于点O,BC=5,若DE∥AC,CE∥BD,则OE的长为_____.
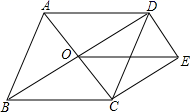
15.如图,边长为1的菱形ABCD中,∠DAB=60°.连结对角线AC,以AC为边作第二个菱形ACEF,使∠FAC=60°.连结AE,再以AE为边作第三个菱形AEGH使∠HAE=60°…按此规律所作的第n个菱形的边长是 .
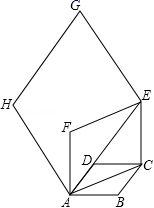
16.如图,在平面直角坐标系中,O为坐标原点,四边形OABC是长方形,点A、C的坐标分别为A(10,0)、C(0,4),点D是OA的中点,点P在BC边上运动,当△ADP为等腰三角形时,点P的坐标为_______________________________.
三、解下列各题(本大题共8小题,共72分)
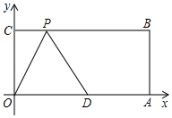
17.(8分)如图,在平行四边形ABCD中,DB=DA,∠ADB的平分线交AB于点F,交CB的延长线于点E,连接AE.
(1)求证:四边形AEBD是菱形;
(2)若DC=![]() ,EF:BF=3,求菱形AEBD的面积.
,EF:BF=3,求菱形AEBD的面积.
18.(8分)如图,在矩形ABCD中,∠BAD的平分线交BC于点E,O为对角线AC、BD的交点,且∠CAE=15° .
(1)求证:△AOB为等边三角形;
(2)求∠BOE度数.
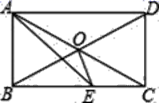
19.(8分)限速安全驾,文明靠大家,根据道路管理条例规定,在某段笔直的公路L上行驶的车辆,限速60千米![]() 时,一观测点M到公路L的距离MN为30米,现测得一辆汽车从A点到B点所用时间为5秒,已知观测点M到A,B两点的距离分别为50米、34米,通过计算判断此车是否超速.
时,一观测点M到公路L的距离MN为30米,现测得一辆汽车从A点到B点所用时间为5秒,已知观测点M到A,B两点的距离分别为50米、34米,通过计算判断此车是否超速.
20.(8分)(1)解方程:![]() =
=![]() ;
;
(2)因式分解:2x2-1.
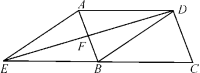
21.(8分)已知:如图,四边形![]() 中,
中,![]() 、
、![]() 、
、![]() 、
、![]() 分别为
分别为![]() 、
、![]() 、
、![]() 和
和![]() 的中点,且
的中点,且![]() .
.
求证:![]() 和
和![]() 互相垂直且平分.
互相垂直且平分.
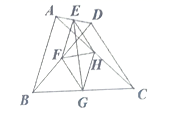
22.(10分)已知正方形![]() 中,
中,![]() 为对角线
为对角线![]() 上一点,过点
上一点,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() 为
为![]() 的中点,连接
的中点,连接![]() .
.
(1)如图1,求证:![]() ;
;
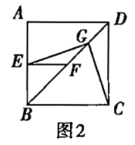
(2)将图1中的![]() 绕点
绕点![]() 逆时针旋转45°,如图2,取
逆时针旋转45°,如图2,取![]() 的中点
的中点![]() ,连接
,连接![]() .问(1)中的结论是否仍然成立?若成立,给出证明;若不成立,请说明理由.
.问(1)中的结论是否仍然成立?若成立,给出证明;若不成立,请说明理由.
(3)将图1中的![]() 绕点
绕点![]() 逆时计旋转任意角度,如图3,取
逆时计旋转任意角度,如图3,取![]() 的中点
的中点![]() ,连接
,连接![]() .问(1)中的结论是否仍然成立?通过观察你还能得出什么结论?(均不要求证明)
.问(1)中的结论是否仍然成立?通过观察你还能得出什么结论?(均不要求证明)

23.(10分)在进行二次根式运算时,我们有时会碰上如![]() 这样的式子,我们还可以将其进一步化简:
这样的式子,我们还可以将其进一步化简: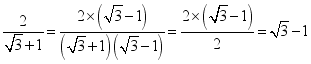 以上这种化简过程叫做分母有理化.
以上这种化简过程叫做分母有理化.![]() 还可以尝试用以下方法化简:
还可以尝试用以下方法化简:
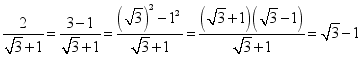
(1)请用两种不同的方法化简;![]()
(2)请任选一种方法化简:![]()
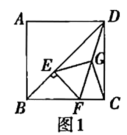
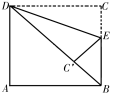
24.(12分)如图,已知正方形ABCD边长为2,E是BC边上一点,将此正方形的一只角DCE沿直线DE折叠,使C点恰好落在对角线BD上,求BE的长.
参考答案
一、选择题(每小题3分,共30分)
1、B
2、C
3、D
4、C
5、B
6、D
7、C
8、D
9、C
10、A
二、填空题(本大题共有6小题,每小题3分,共18分)
11、2.1
12、4
13、AC⊥BD
14、1
15、![]()
16、 (2,4),(8,4),(7,4),(7.5,4)
三、解下列各题(本大题共8小题,共72分)
17、(1)见解析;(2)1.
18、(1)见解析;(2)75°
19、此车没有超速
20、(1)x=-10;(2)2(x+2)(x-2)
21、见解析.
22、 (1)见解析;(2)见解析;(3)见解析.
23、(1)![]() ;(2)
;(2)![]() .
.
24、BE=![]() .
.
2023-2024学年江苏无锡梁溪区四校联考九上数学期末达标检测试题含答案: 这是一份2023-2024学年江苏无锡梁溪区四校联考九上数学期末达标检测试题含答案,共8页。试卷主要包含了已知函数y=ax2+bx+c,计算的值为,计算的结果是等内容,欢迎下载使用。
江苏无锡梁溪区四校联考2023-2024学年数学八上期末复习检测试题含答案: 这是一份江苏无锡梁溪区四校联考2023-2024学年数学八上期末复习检测试题含答案,共6页。试卷主要包含了已知,则的值是,下列运算正确的是等内容,欢迎下载使用。
2022-2023学年江苏省无锡市梁溪区七年级(上)期末数学试卷: 这是一份2022-2023学年江苏省无锡市梁溪区七年级(上)期末数学试卷,共19页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












